Estadística inferencial

La estadística descriptiva y la estadística inferencial son dos subcampos de la estadística. La estadística descriptiva incluye temas tratados anteriormente en este camino, incluidos resúmenes numéricos y visuales de datos. La prueba de hipótesis, por otro lado, es una forma de estadística inferencial, que se utiliza para hacer inferencias sobre una población utilizando una muestra más pequeña de datos.

Esto es importante porque las estadísticas descriptivas pueden informarnos sobre los datos que tenemos, pero a veces no podemos recopilar todos los datos que necesitamos para responder nuestras preguntas. Por ejemplo, tal vez queramos saber si las personas que reciben una vacuna tienen menos probabilidades de contraer una enfermedad. No podemos vacunar a todas las personas del mundo para probar esto, por lo que tendremos que vacunar a una muestra más pequeña de personas. Luego, si la vacuna parece funcionar en nuestra muestra, necesitamos saber si pudo haber sido una casualidad aleatoria o si es probable que sea cierto para el resto de la población. ¡Aquí es donde las pruebas de hipótesis pueden ayudar!

La estadística inferencial consiste en utilizar una muestra (un subconjunto de una población) para hacer inferencias sobre una población de interés más grande. Esto es útil cuando queremos saber algo sobre una población pero no podemos observar a todos sus miembros, a menudo debido a limitaciones de tiempo, viabilidad o monetarias. Algunos métodos que se utilizan en estadística inferencial incluyen la prueba de hipótesis y la regresión.

La clave de la estadística inferencial es comprender que las muestras no siempre reflejan con precisión la población de la que proceden. Una gran parte de la estadística inferencial consiste en cuantificar nuestra incertidumbre sobre una población observando una muestra más pequeña.

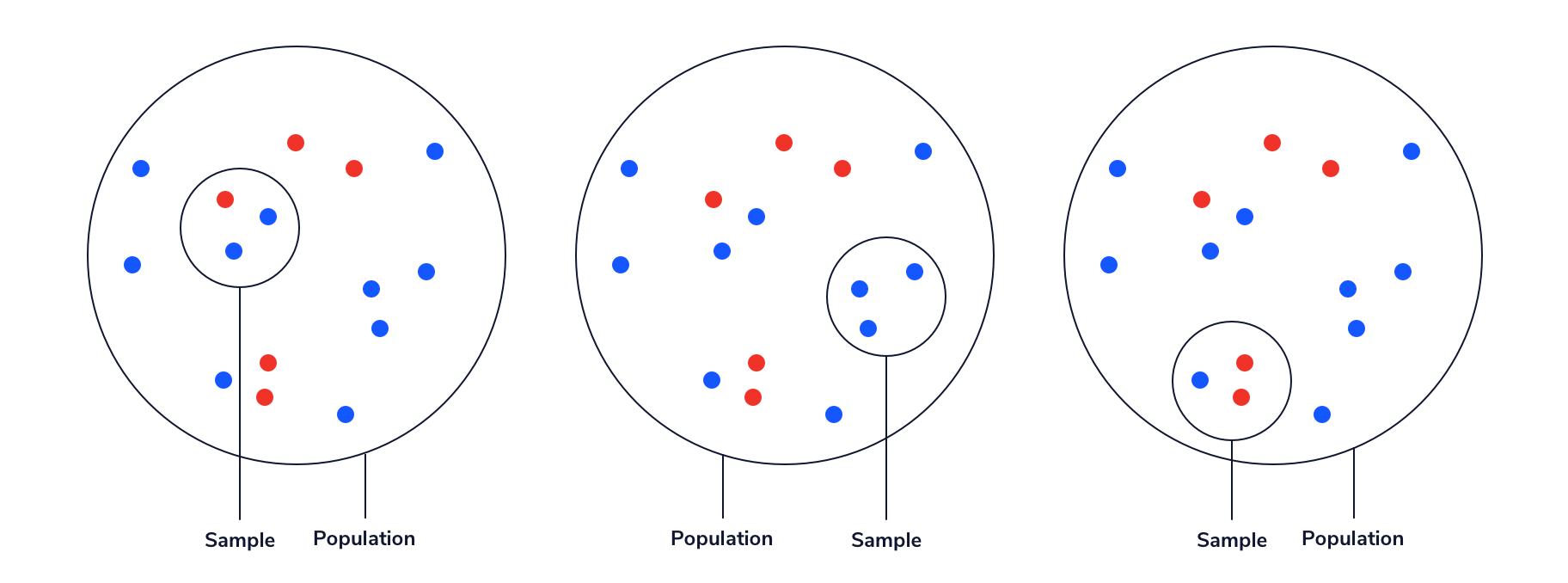
Por ejemplo, la población que se muestra a continuación se compone de 10 puntos azules y 5 puntos rojos, lo que significa que dos tercios de la población es azul y un tercio es rojo. Supongamos que tomamos una muestra aleatoria de 3 puntos y queremos usar esa muestra para estimar la proporción de la población que es azul. Si tenemos suerte, tomaremos una muestra de 2 puntos azules y 1 punto rojo, como se muestra a la izquierda, lo que representaría con precisión las proporciones de puntos azules y rojos en la población. Sin embargo, también podríamos muestrear aleatoriamente 3 puntos azules, o 2 puntos rojos y 1 punto azul, los cuales no coinciden con la población. La estadística inferencial nos permite observar una muestra y luego cuantificar nuestra incertidumbre sobre cuán similar (o diferente) podría ser toda la población.

Ejemplo: contacto con el cliente

Suponga que trabaja en una empresa de ventas que está interesada en probar dos métodos diferentes de contacto con el cliente para ver si uno genera una tasa de respuesta más alta que el otro. Es imposible probar ambos métodos con toda la población de cada cliente pasado, presente y futuro. En su lugar, podría tomar una muestra de 1000 clientes y asignarlos aleatoriamente a un sistema de contacto por mensaje de texto o a un sistema de llamadas telefónicas. Después de un mes, podría calcular la diferencia en la tasa de respuesta (una estadística descriptiva) para los dos grupos de la muestra.

Suponga que descubre que los clientes que recibieron un mensaje de texto tenían un 12% más de probabilidades de responder que los clientes que recibieron una llamada telefónica. Esta es una estadística descriptiva de la muestra, pero lo que realmente desea saber es: si hubiera muestreado a toda la población de clientes, ¿habría encontrado al menos una diferencia del 12 % en la tasa de respuesta?

¡Aquí es donde los métodos de estadística inferencial resultan útiles! Por ejemplo, podría utilizar una prueba de hipótesis para estimar la probabilidad de que, en toda la población, observe una tasa de respuesta más alta para los mensajes de texto en comparación con las llamadas, dado que observó una tasa más alta en su muestra.

Ejemplo: puntuaciones de exámenes

Supongamos que usted es un investigador que estudia la relación entre las calificaciones de las tareas de los estudiantes de secundaria y los puntajes de las pruebas estandarizadas. Sería muy difícil y costoso recopilar información sobre las calificaciones de las tareas y los resultados de los exámenes estandarizados de cada estudiante de secundaria del mundo. En su lugar, podría encontrar una muestra aleatoria de estudiantes e inspeccionar la relación entre las calificaciones de las tareas y los puntajes de las pruebas estandarizadas entre esa muestra. Finalmente, podría utilizar un análisis de regresión (otro método estadístico inferencial) para comprender si es probable que exista una relación similar en la población más grande de todos los estudiantes.

Elementos clave en una prueba de hipótesis:

1. Hipótesis nula \(H_0\):
   • Es una declaración inicial que se asume verdadera a menos que los datos muestrales provean evidencia en contra.
   • Suele expresar “no hay efecto” o “no hay diferencia”.
   • Ejemplo: “La media de una población es igual a 50.”
2. Hipótesis alternativa \(H_1\) o \(H_A\):
   • Es una declaración opuesta a la hipótesis nula, la cual se busca demostrar.
   • Representa lo que esperamos encontrar en nuestros análisis.
   • Ejemplo: “La media de una población es diferente de 50.”
3. Nivel de significancia \(\alpha\):
   • Es el umbral que establece la probabilidad de rechazar incorrectamente la hipótesis nula (error de Tipo I).
   • Un valor comúnmente usado es \(0.05\) (5%).
4. Estadístico de prueba:
   • Una medida cuantitativa que se calcula a partir de los datos muestrales y que se usa para evaluar la hipótesis.
   • Su cálculo depende del tipo de prueba (t, z, chi-cuadrado, etc.).
5. Valor p:
   • Es la probabilidad de obtener un resultado al menos tan extremo como el observado, bajo la suposición de que la hipótesis nula es verdadera.
   • Si el valor p es menor que el nivel de significancia \(\alpha\), se rechaza la hipótesis nula en favor de la hipótesis alternativa.

Pasos para una prueba de hipótesis:

1. Definir las hipótesis: Formular claramente las hipótesis nula y alternativa.

2. Seleccionar el nivel de significancia: Decidir el nivel \(\alpha\), normalmente 0.05.

3. Elegir el tipo de prueba:
   • Puede ser una prueba t, z, chi-cuadrado, ANOVA, etc., según el tipo de datos y la pregunta de investigación.
4. Recolectar y analizar datos:
   • Calcular el estadístico de prueba con los datos muestrales.
5. Interpretar resultados:
   • Comparar el valor p con el nivel de significancia.
   • Si el valor p es menor que \(\alpha\), rechazar \(H_0\).
   • Si el valor p es mayor o igual que \(\alpha\), no hay suficiente evidencia para rechazar \(H_0\).

Estadisticos de Prueba

Los estadísticos de prueba son fundamentales en el análisis de pruebas de hipótesis y varían según el tipo de datos y la naturaleza de la hipótesis que se está probando.

t de Student

La prueba t-Student para una muestra es una técnica utilizada para determinar si la media de una muestra es estadísticamente diferente de una media poblacional conocida o hipotética. Esta prueba se utiliza cuando la población no sigue una distribución normal o cuando el tamaño de la muestra es pequeño (menos de 30).

En resumen, la prueba t-Student para una muestra es una herramienta útil para analizar si una muestra de datos es representativa de una población más grande y para determinar si la diferencia entre la media de la muestra y la media poblacional es significativa desde un punto de vista estadístico.

Tipos de prueba t-Student

Hay varios tipos de pruebas t de Student, cada uno diseñado para abordar una situación particular. Los tipos más comunes de pruebas t de Student son:

• Prueba t de dos muestras para datos independientes: Esta prueba se utiliza cuando se quieren comparar las medias de dos grupos independientes, es decir, cuando las observaciones en un grupo no están relacionadas de ninguna manera con las observaciones en el otro grupo. Por ejemplo, se podría usar para comparar las calificaciones promedio de dos grupos de estudiantes que tomaron diferentes cursos.

• Prueba t de dos muestras para datos relacionados o emparejados: En este caso, se comparan las medias de dos grupos que están relacionados de alguna manera, como las mediciones antes y después de un tratamiento en el mismo grupo de individuos. También se conoce como «prueba t de muestras relacionadas» o «prueba t emparejada».

• Prueba t de una muestra: Esta prueba se utiliza cuando se quiere comparar la media de una sola muestra con un valor de referencia conocido o hipotético (por ejemplo, la media poblacional). Se utiliza para determinar si la muestra difiere significativamente de la media hipotética.

• Prueba t de varianzas iguales o heterogéneas: La mayoría de las pruebas t de Student asumen que las varianzas de los dos grupos que se comparan son iguales. Sin embargo, en ocasiones, esta suposición puede no cumplirse. La prueba t de varianzas iguales se utiliza cuando se asume que las varianzas son iguales, mientras que la prueba t de varianzas heterogéneas se utiliza cuando se asume que las varianzas son diferentes entre los dos grupos.

• Prueba t de una cola o de dos colas: Las pruebas t de Student pueden ser de una cola o de dos colas, dependiendo de la naturaleza de la pregunta de investigación. Una prueba de una cola se utiliza cuando se está interesado en determinar si una media es significativamente mayor o menor que otra, mientras que una prueba de dos colas se utiliza para detectar cualquier diferencia significativa entre las medias, ya sea mayor o menor.

Simulación de una prueba T de una muestra

La prueba de hipótesis es un marco para hacer preguntas sobre un conjunto de datos y responderlas con declaraciones probabilísticas. Existen muchos tipos diferentes de pruebas de hipótesis que se pueden utilizar para abordar diferentes tipos de preguntas y datos. En este artículo, analizaremos una simulación de una prueba t de una muestra para desarrollar una intuición sobre cuántos tipos diferentes de pruebas de hipótesis funcionan.

El Caso

El Programa de Bachillerato Internacional (IBDP) es un programa educativo a nivel mundial. Cada año, los estudiantes de las escuelas participantes pueden realizar una evaluación estandarizada para obtener su título. Las puntuaciones totales de esta evaluación oscilan entre 1 y 45. Según los datos proporcionados aquí , la puntuación total promedio de todos los estudiantes que tomaron este examen en mayo de 2020 fue de alrededor de 29,92. La distribución de puntuaciones se parece a esto:

Imagine una hipotética escuela en línea, Statistics Academy, que ofrece un programa de preparación para exámenes de cinco semanas. Supongamos que 100 estudiantes que tomaron la evaluación del IBDP en mayo de 2020 fueron elegidos al azar para participar en el primer grupo de este programa y que estos 100 estudiantes obtuvieron una puntuación promedio de 31,16 puntos en el examen, ¡aproximadamente 1,24 puntos más que el promedio internacional!

¿Estos estudiantes realmente están superando a sus compañeros? ¿O podría atribuirse esta diferencia al azar?

Paso 2: definir las hipótesis nula y alternativa

Antes de intentar responder esta pregunta, es útil reformularla de manera que sea comprobable. En este momento, nuestra pregunta (“¿Los estudiantes de la Academia de Estadística realmente están superando a sus compañeros?”) no está claramente definida.

Una prueba de hipótesis comienza con dos hipótesis en competencia sobre la población de la que proviene una muestra particular (en este caso, los 100 estudiantes de la Academia de Estadística):

Hipótesis Nula \(H_0\): Los 100 estudiantes de la Academia de Estadística son una muestra aleatoria de la población general de examinados, que obtuvieron una puntuación promedio de 29,92.

Si esta hipótesis es cierta, los estudiantes de la Academia de Estadística obtuvieron una puntuación promedio ligeramente más alta por casualidad. Visualmente, esta configuración se parece a esto:

Hipótesis Alternativa \(H_1\): Los 100 estudiantes de la Academia de Estadística provenían de una población con una puntuación promedio diferente de 29,92.

En esta hipótesis, debemos imaginar dos poblaciones diferentes que en realidad no existen: una en la que todos los estudiantes tomaron el programa de preparación para exámenes de la Academia de Estadística y otra en la que ninguno de los estudiantes tomó el programa. Si la hipótesis alternativa es cierta, nuestra muestra de 100 estudiantes de la Academia de Estadística provenía de una población diferente a la de los demás examinados.

Hay una aclaración más que debemos hacer para especificar completamente la hipótesis alternativa. Observe que, hasta ahora, no hemos dicho nada sobre el puntaje promedio para la “población 1” en el diagrama anterior, aparte de que NO es 29,92. En realidad, tenemos tres opciones para lo que dice la hipótesis alternativa sobre este promedio poblacional:

• es MAYOR QUE 29.92
• NO ES IGUAL A (es decir, MAYOR O MENOR QUE) 29,92
• es MENOS DE 29,92

Más adelante, analizaremos cómo la elección entre “mayor que”, “distinto de” y “menor que” afecta la prueba.

Paso 3: determinar la distribución nula

Ahora que tenemos nuestra hipótesis nula, podemos generar una distribución nula : la distribución (entre muestras repetidas) de la estadística que nos interesa si la hipótesis nula es verdadera. En el ejemplo del IBDP descrito anteriormente, esta es la distribución de puntuaciones promedio para muestras repetidas de tamaño 100 extraídas de una población con una puntuación promedio de 29,92.

¡Esto puede resultarle familiar si ha aprendido sobre el teorema del límite central (CLT)! La teoría estadística nos permite estimar la forma de esta distribución utilizando una sola muestra. Puede aprender cómo hacer esto leyendo más sobre CLT, pero para los propósitos de este ejemplo, simulemos la distribución nula usando nuestra población. Podemos hacer esto mediante:

• Tomar muchas muestras aleatorias de 100 puntuaciones, cada una, de la población.
• Calcular y almacenar la puntuación promedio para cada una de esas muestras.
• Trazar un histograma de las puntuaciones medias

Esto produce la siguiente distribución, que es aproximadamente normal y centrada en el promedio de la población:

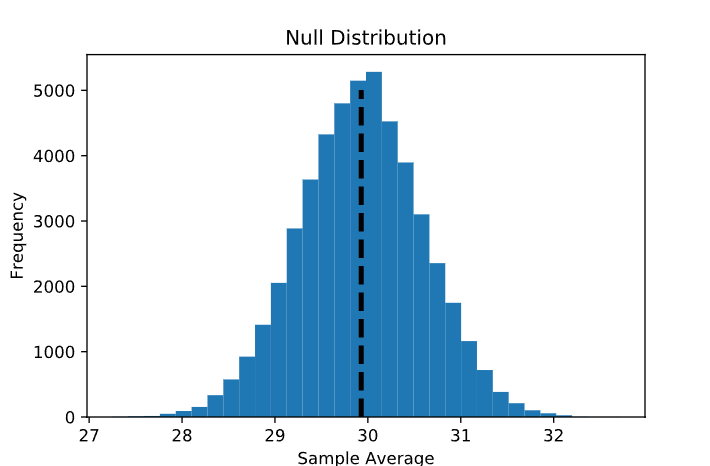
Si la hipótesis nula es cierta, entonces la puntuación promedio de 31,16 observada entre los estudiantes de la Academia de Estadística es simplemente uno de los valores de esta distribución. Tracemos el promedio muestral en la distribución nula. Observe que este valor está dentro del rango de la distribución nula, pero está hacia la derecha donde hay menos densidad:

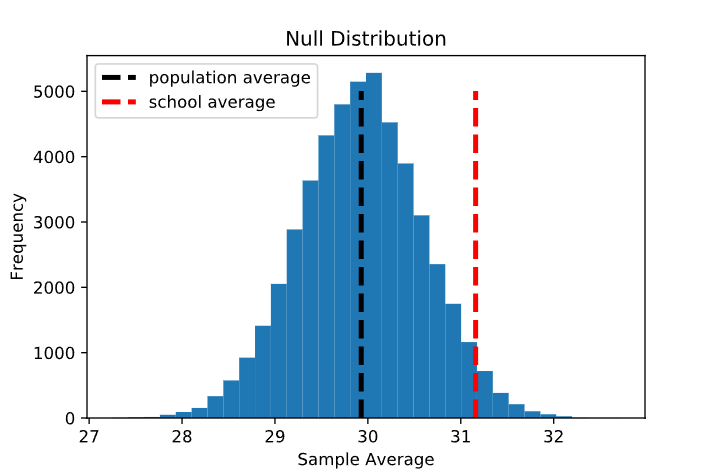
Paso 4: Calcule un valor P (o intervalo de confianza)

Aquí está la pregunta básica formulada en nuestra prueba de hipótesis:

Dado que la hipótesis nula es cierta (que los 100 estudiantes de la Academia de Estadística fueron seleccionados de una población con una puntuación promedio del IBDP de 29,92), ¿qué probabilidad hay de que su puntuación promedio sea 31,16?

El problema menor de esta pregunta es que la probabilidad de cualquier puntuación promedio exacta es muy pequeña, por lo que realmente queremos estimar la probabilidad de un rango de puntuaciones. Volvamos ahora a nuestras tres posibles hipótesis alternativas y veamos cómo la pregunta y el cálculo cambian ligeramente, dependiendo de cuál elijamos:

Opción 1

Hipótesis alternativa: La muestra de 100 puntajes obtenidos por estudiantes de la Academia de Estadística provino de una población con un puntaje promedio superior a 29,92.

En este caso, queremos saber la probabilidad de observar un promedio muestral mayor o igual a 31,16 dado que la hipótesis nula es verdadera. Visualmente, esta es la proporción de la distribución nula que es mayor o igual a 31,16 (sombreada en rojo a continuación). Aquí, la región roja representa alrededor del 3,1% de la distribución total. Esta proporción, que normalmente se escribe en forma decimal (es decir, 0,031), se denomina valor p .

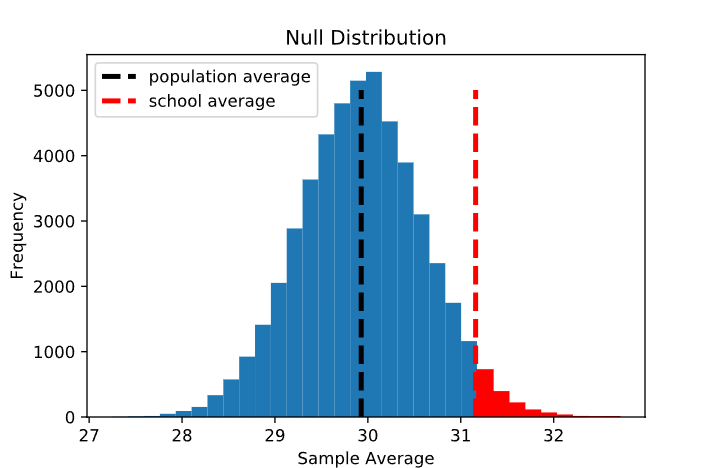
opcion 2

Hipótesis alternativa: La muestra de 100 puntajes obtenidos por estudiantes de la Academia de Estadística provino de una población con un puntaje promedio que no es igual (es decir, mayor o menor que) 29,92.

Observamos un promedio muestral de 31,16 entre los estudiantes de la Academia de Estadística, que es 1,24 puntos más alto que el promedio poblacional (si la hipótesis nula es cierta) de 29,92. En la primera versión de la prueba de hipótesis (opción 1), estimamos la probabilidad de observar un promedio muestral que sea al menos 1,24 puntos mayor que el promedio poblacional.

Para la hipótesis alternativa descrita en la opción 2, nos interesa la probabilidad de observar un promedio de muestra que sea al menos 1,24 puntos DIFERENTE (mayor O menor) que el promedio de la población. Visualmente, esta es la proporción de la distribución nula que está al menos a 1,24 unidades del promedio de la población (sombreado en rojo a continuación). Tenga en cuenta que esta área es dos veces mayor que en el ejemplo anterior, lo que lleva a un valor p que también es dos veces mayor: 0,062.

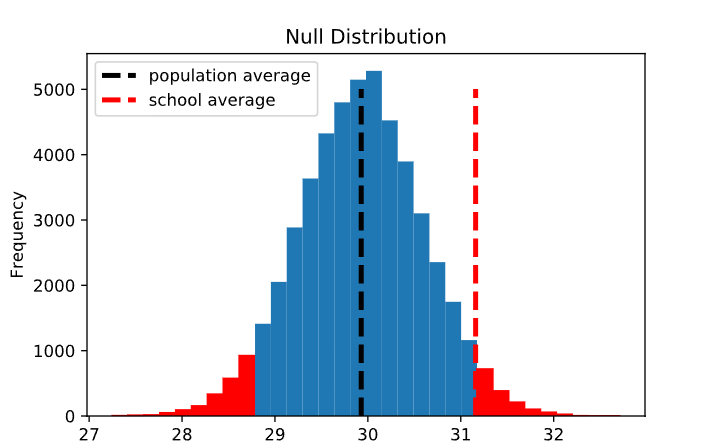
Si bien la opción 1 a menudo se conoce como prueba de una cara o de una cola , esta versión se conoce como prueba de dos caras o de dos colas , y hace referencia a las dos colas de la distribución nula que se cuentan en el valor p. Es importante tener en cuenta que la mayoría de las funciones de prueba de hipótesis en Python y R implementan una prueba de dos colas de forma predeterminada.

Opción 3

Hipótesis alternativa: La muestra de 100 puntajes obtenidos por estudiantes de la Academia de Estadística provino de una población con un puntaje promedio inferior a 29,92.

Aquí queremos saber la probabilidad de observar un promedio muestral menor o igual a 31,16, dado que la hipótesis nula es verdadera. Esta también es una prueba unilateral, justo el lado opuesto de la opción 1. Visualmente, esta es la proporción de la distribución nula que es menor o igual a 31,16. Esta es un área muy grande (¡casi el 97% de la distribución!), lo que lleva a un valor p de 0,969.

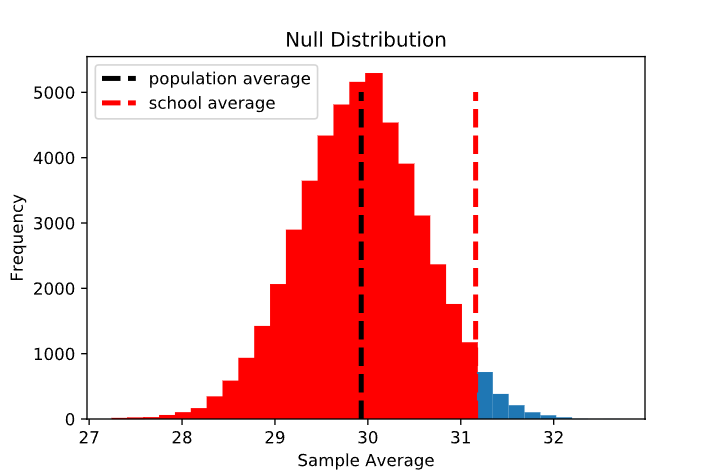
En este punto, usted puede estar pensando: ¿por qué alguien elegiría esta versión de la hipótesis alternativa? En la vida real, si un programa de preparación de exámenes planeaba realizar un experimento riguroso para ver si sus estudiantes obtienen calificaciones diferentes a las de la población general, deberían elegir la hipótesis alternativa antes de recopilar datos. En ese momento, no sabrán si su muestra de estudiantes tendrá una puntuación promedio mayor o menor que el promedio de la población, aunque probablemente esperan que sea mayor.

Paso 5: interpretar los resultados

En los tres ejemplos anteriores, se calcularon tres valores p diferentes (0,031, 0,062 y 0,969, respectivamente). Considere el primer valor p de 0,031. La interpretación de este número es la siguiente:

Si los 100 estudiantes de la Academia de Estadística fueron seleccionados al azar de toda la población (que obtuvo una puntuación promedio de 29,92), hay un 3,1% de posibilidades de que su puntuación promedio sea de 31,16 puntos o más.

Esto significa que es relativamente improbable, pero no imposible, que los estudiantes de la Academia de Estadística obtengan puntuaciones más altas (en promedio) que sus compañeros por casualidad, a pesar de que no hay una diferencia real a nivel de población.

En otras palabras, los datos observados son improbables si la hipótesis nula es cierta. Tenga en cuenta que hemos probado directamente la hipótesis nula, ¡pero no la hipótesis alternativa! Por lo tanto, debemos tener un poco de cuidado al interpretar esta prueba: no podemos decir que hemos demostrado que la hipótesis alternativa es la verdad, sólo que los datos que recopilamos serían improbables bajo la hipótesis nula y, por lo tanto, creemos que la hipótesis alternativa es cierta. La hipótesis alternativa es más consistente con nuestras observaciones.

Umbrales de significancia

Si bien es perfectamente razonable informar un valor \(p\), muchos científicos de datos utilizan un umbral predeterminado para decidir si un valor \(p\) particular es significativo o no. Los valores P por debajo del umbral elegido se declaran significativos y llevan al científico de datos a “rechazar la hipótesis nula en favor de la alternativa”. Una elección común para este umbral, que a veces también se denomina Alfa , es 0,05, ¡pero es una elección arbitraria! Usar un umbral más bajo significa que es menos probable que encuentre resultados significativos, pero también es menos probable que informe erróneamente un resultado significativo cuando no lo hay.

Utilizando el primer valor p de 0,031 y un umbral de significancia de 0,05, la Academia de Estadística podría rechazar la hipótesis nula y concluir que los 100 estudiantes que participaron en su programa obtuvieron puntuaciones significativamente más altas en la prueba que la población general.

Impacto de la hipótesis alternativa

Tenga en cuenta que diferentes hipótesis alternativas pueden llevar a conclusiones diferentes. Por ejemplo, la prueba unilateral descrita anteriormente (p = 0,031) llevaría a un científico de datos a rechazar la nula en un nivel de significancia de 0,05. Mientras tanto, una prueba bilateral sobre los mismos datos conduce a un valor p de 0,062, que es mayor que el umbral de 0,05. Por tanto, para la prueba bilateral, un científico de datos no podría rechazar la hipótesis nula. ¡Esto resalta la importancia de elegir una hipótesis alternativa con anticipación!

Resumen y aplicaciones adicionales

Como seguramente habrá aprendido de este artículo, las pruebas de hipótesis pueden ser un marco útil para formular y responder preguntas sobre datos. Antes de utilizar las pruebas de hipótesis en la práctica, es importante recordar lo siguiente:

• Un valor \(p\) es una probabilidad, generalmente expresada como un decimal entre cero y uno.
• Un valor \(p\) pequeño significa que es poco probable que ocurra una estadística de muestra observada (o algo más extremo) si la hipótesis nula es cierta.
• Se puede utilizar un umbral de significancia para traducir un valor p en un resultado “significativo” o “no significativo”.
• En la práctica, la hipótesis alternativa y el umbral de significancia deben elegirse antes de la recopilación de datos.

Implementación de una prueba t de una muestra en Python

Las pruebas t de una muestra se utilizan para comparar un promedio de muestra con un promedio de población hipotético. Por ejemplo, se podría utilizar una prueba t de una muestra para abordar preguntas como:

• ¿La cantidad de tiempo promedio que los visitantes pasan en un sitio web es diferente de 5 minutos?
• ¿La cantidad promedio de dinero que gastan los clientes en una compra es superior a 10 USD?

Como ejemplo, imaginemos la empresa ficticia BuyPie, que envía ingredientes para pasteles a tu casa para que puedas prepararlos desde cero. Supongamos que un gerente de producto quiere que los pedidos en línea de BuyPie cuesten alrededor de 1000 rupias en promedio. El día anterior, 50 personas realizaron una compra en línea y el pago promedio por pedido fue inferior a 1000 rupias. ¿La gente realmente gasta menos de 1000 rupias en promedio? ¿O es esto el resultado del azar y de un tamaño de muestra pequeño?

# Ventas del dia anterior
ventas = [ 978. 1080.  999.  855. 1105.  961.  899. 1061.  880. 1455.  505.  936.
 1024.  982.  840.  930.  829.  504.  955. 1380. 1361. 1130.  946.  973.
 1076. 1131.  810.  734. 1275.  867.  962.  865.  709. 1216.  735.  768.
  757. 1060.  715.  839.  999. 1259. 1194. 1082. 1129. 1255.  931. 1236.
  921.  907.]

import numpy as np

# calculate prices_mean and print it out:
prices_mean = np.mean(prices)
print(f'Mean: {prices_mean}')

Salida

Mean: 980.0

Al inspeccionar la muestra de 50 precios de compra en BuyPie y vimos que el promedio era de 980.0 rupias. Supongamos que queremos ejecutar una prueba \(t\) para una muestra con las siguientes hipótesis nula y alternativa:

• Nulo: el coste medio de un pedido de BuyPie es de 1000 rupias.
• Alternativa: el coste medio de un pedido de BuyPie no es de 1000 rupias.

SciPy tiene una función llamada ttest_1samp(), que realiza una prueba \(t\) de una muestra. Esta funcion requiere dos entradas, una distribución de la muestra (por ejemplo, la lista de los 50 precios de compra observados) y una media para comparar (por ejemplo 1000):

tstat, pval = ttest_1samp(sample_distribution, expected_mean)

La función utiliza su distribución muestral para determinar el tamaño de la muestra y estimar la cantidad de variación en la población, que se utilizan para estimar la distribución nula. Devuelve dos resultados:

• tstat: el estadístico \(t\) (que no cubriremos en este curso)
• pval: el valor \(p\).

tstat, pval = ttest_1samp(ventas, 1000)
print(f'Valor de p: {pval}')

Salida:

Valor de p: 0.4920744804182786

Los valores p son probabilidades, por lo que deben estar entre 0 y 1. Este valor p es la probabilidad de observar un precio de compra promedio inferior a 980 O superior a 1020 entre una muestra de 50 compras. Si ejecuta la prueba correctamente, debería ver un valor p de 0,49 o 49%.

Dado que el precio de compra medio en esta muestra fue 980, que no está muy lejos de 1000, probablemente esperamos que este valor p sea relativamente grande. La única razón por la que PODRÍA ser pequeño (por ejemplo, <0,05) es si los precios de compra tuvieran muy poca variación (por ejemplo, todos estaban dentro de unas pocas rupias de 980). Podemos ver en los datos impresos que este no es el caso. Por lo tanto, ¡un valor p de alrededor de 0,49 tiene sentido!

Supuestos de una prueba T de una muestra

Al ejecutar cualquier prueba de hipótesis, es importante conocer y verificar los supuestos de la prueba. Los supuestos de una prueba \(t\) de una muestra son los siguientes:

• La muestra fue seleccionada aleatoriamente de la población: Por ejemplo, si solo recopila datos de los visitantes del sitio que aceptan compartir su información personal, este subconjunto de visitantes no se seleccionó al azar y puede diferir de la población más grande.
• Las observaciones individuales fueron independientes: Por ejemplo, si a un visitante de BuyPie le encanta tanto la tarta de manzana que compró que convenció a su amigo para que también comprara una, esas observaciones no fueron independientes.
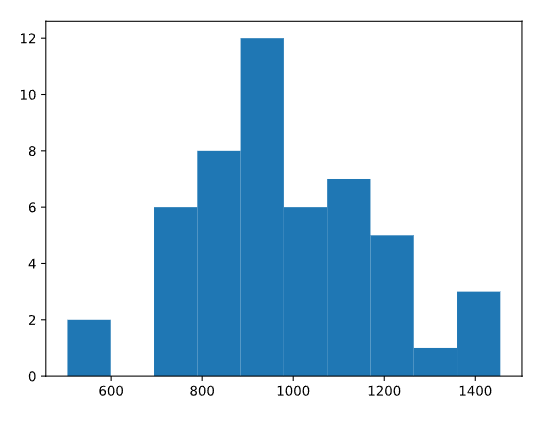
• Los datos se distribuyen normalmente sin valores atípicos O el tamaño de la muestra es suficiente grande: No existen reglas establecidas sobre qué es un tamaño de muestra “suficientemente grande”, pero un umbral común es alrededor de 40. Para tamaños de muestra menores a 40, y en realidad para todas las muestras en general, es una buena idea asegurarse de trazar un histograma de sus datos y verifique si hay valores atípicos, distribuciones multimodales (con múltiples jorobas) o distribuciones sesgadas. Si ve alguna de esas cosas en una muestra pequeña, una prueba t probablemente no sea apropiada.

En general, si ejecuta un experimento que viola (o posiblemente viola) una de estas suposiciones, aún puede ejecutar la prueba e informar los resultados, pero también debe informar las suposiciones que no se cumplieron y reconocer que los resultados de la prueba podrían ser defectuosos.

Simulación de una prueba de hipótesis binomial en Python

Las pruebas binomiales son útiles para comparar la frecuencia de algún resultado en una muestra con la probabilidad esperada de ese resultado. Por ejemplo, si esperamos que el 90% de los pasajeros con boleto se presenten a su vuelo, pero solo 80 de 100 pasajeros con boleto realmente se presentan, podríamos usar una prueba binomial para comprender si 80 es significativamente diferente de 90.

Las pruebas binomiales son similares a las pruebas \(t\) de una muestra en el sentido de que comparan una estadística de muestra con alguna expectativa a nivel de población. La diferencia es que:

• Las pruebas binomiales se utilizan para datos categóricos binarios para comparar una frecuencia de muestra con una probabilidad esperada a nivel de población.
• Las pruebas \(t\) de una muestra se utilizan para datos cuantitativos para comparar la media de una muestra con una media poblacional esperada.

En Python, como en muchos otros lenguajes de programación utilizados para la computación estadística, hay una serie de bibliotecas y funciones que permiten a un científico de datos ejecutar una prueba de hipótesis en una sola línea de código. Sin embargo, será mucho más probable que un científico de datos detecte y corrija errores potenciales e interprete los resultados correctamente si tiene una comprensión conceptual de cómo funcionan estas funciones.

Los siguientes ejercicios recorrerán el proceso de utilizar una prueba binomial para analizar datos de una hipotética empresa en línea, Live-it-LIVE.com, un sitio web que vende todos los accesorios y disfraces necesarios para recrear escenas icónicas de películas en casa.

Resumiendo la muestra

El departamento de marketing de Live-it-LIVE informa que, durante esta época del año, alrededor del 10% de los visitantes de Live-it-LIVE.com realizan una compra.

El informe mensual muestra a todos los visitantes del sitio y si realizaron o no una compra. La página de pago tuvo un pequeño error este mes, por lo que el departamento comercial quiere saber si la tasa de compra cayó por debajo de las expectativas. Nos han pedido que investiguemos esta cuestión.

Para ejecutar una prueba de hipótesis para abordar esto, primero necesitaremos saber dos cosas a partir de los datos:

• El número de personas que visitaron el sitio web.
• El número de personas que realizaron una compra en el sitio web.

Suponiendo que cada fila de nuestro conjunto de datos representa un visitante único del sitio, podemos calcular la cantidad de personas que visitaron el sitio web encontrando la cantidad de filas en el marco de datos. Luego podemos encontrar el número de personas que realizaron una compra utilizando una declaración condicional para sumar el número total de filas donde se realizó una compra.

# tamaño de la muestra
sample_size = len(monthly_report)
print(f'El tamaño de la muestra: {sample_size}')

# tamaño de los que realizaron compra
num_purchased = (monthly_report['purchase'] == 'y').sum()
print(f'Muestra de los que compraron: {num_purchased}')

Salida

El tamaño de la muestra: 500
Muestra de los que compraron: 41

Simulando aleatoriedad

Calculamos que hubo 500 visitantes del sitio live-it-LIVE.com este mes y 41 de ellos realizaron una compra. En comparación, si cada uno de los 500 visitantes tuviera un 10% de posibilidades de realizar una compra, esperaríamos que alrededor de 50 de esos visitantes compraran algo. ¿Es 41 lo suficientemente diferente de 50 como para que debamos preguntarnos si los visitantes del sitio de este mes realmente tuvieron un 10% de posibilidades de realizar una compra?

Para conceptualizar por qué nuestra expectativa (50) y nuestra observación (41) podrían no ser iguales (AUNQUE no hubiera una caída en la probabilidad de compra), veamos un ejemplo de probabilidad común: lanzar una moneda justa. Podemos simular un lanzamiento de moneda en Python usando la función numpy.random.choice():

one_visitor = np.random.choice(['y', 'n'], size=1, p=[0.1, 0.9])
print(one_visitor)

Utilice la random.choice()función de NumPy para simular 500 visitante de Live-it-LIVE.com, que tiene un 10 % de posibilidades de realizar una compra (p=0,1). Guarde el resultado como una variable con nombre one_visitor. Si el visitante realizó una compra, el valor de one_visitordebe ser [‘y’]; si no hicieron una compra, debería ser así ‘n’.

one_visitor = np.random.choice(['y', 'n'], size=500, p=[0.1, 0.9])
print(one_visitor)

Simulando la distribución nula I

El primer paso para realizar una prueba de hipótesis es formular una hipótesis nula . Para la pregunta de si la tasa de compra en Live-it-LIVE.com fue diferente del 10% este mes, la hipótesis nula describe un mundo en el que la probabilidad real de que un visitante realice una compra fue exactamente del 10%, pero por casualidad. , observamos que sólo 41 visitantes (8,2%) realizaron una compra.

Volvamos al ejemplo del lanzamiento de moneda del ejercicio anterior. Podemos simular 10 lanzamientos de moneda e imprimir el número de esos lanzamientos que salieron cara usando el siguiente código:

import numpy as np
import pandas as pd

null_outcomes = []


for i in range(10000):
  simulated_monthly_visitors = np.random.choice(['y', 'n'], size=500, p=[0.1, 0.9])
  num_purchased = np.sum(simulated_monthly_visitors == 'y')
  null_outcomes.append(num_purchased)


#calculate the minimum and maximum values in null_outcomes here:
null_min = min(null_outcomes)
null_max = max(null_outcomes)
print(f'El minimo es:  {null_min}')
print(f'El maximo es:  {null_max}')

Salida

El mínimo es: 28
El máximo es: 78

Inspeccionando la distribución nula

En el ejercicio anterior, simulamos 10000 muestras diferentes de 500 visitantes, donde cada visitante tenía un 10% de posibilidades de realizar una compra, y calculamos el número de compras por muestra. Tras una inspección más detallada, vimos que esos números oscilaban entre 32 y 78. Esta es información útil, pero podemos aprender aún más al inspeccionar la distribución completa.

Podemos trazar un histograma de null_outcomes uso matplotlib.pyplot.hist(). También podemos agregar una línea vertical en cualquier valor de x usando matplotlib.pyplot.axvline():

plt.hist(null_outcomes)
plt.axvline(41, color = 'r')
plt.show()

Este histograma nos muestra 10.000 experimentos, en el mes que estamos investigando calculamos que hubo 41 compras. ¿Dónde queda 41 en esta distribución? ¿Es relativamente probable o improbable?

Intervalos de confianza

Hasta ahora, hemos inspeccionado la distribución nula y calculado los valores mínimo y máximo. Si bien el número de compras en cada muestra simulada osciló aproximadamente entre 32 y 778 por azar, tras una inspección más detallada de la distribución, vimos que esos valores extremos ocurrían muy raramente.

Calculamos los percentiles 5 y 95 de modo que exactamente el 10% de los datos quedan fuera de esos percentiles. Esto nos deja con un rango que cubre el 90% de los datos.

Si nuestra estadística observada queda fuera de este intervalo, entonces podemos concluir que es poco probable que la hipótesis nula sea cierta. En este ejemplo, debido a que 41 se encuentra dentro del intervalo del 90%, todavía es razonablemente probable que hayamos observado una tasa de compra más baja por casualidad, aunque la hipótesis nula fuera cierta.

Al informar un intervalo que cubre el 90% de los valores en lugar del rango completo, podemos decir algo como: “tenemos un 90% de confianza en que, si cada visitante tiene un 10% de posibilidades de realizar una compra, una muestra aleatoria de 500 visitantes lo hará”. realizar entre 37 y 63 compras”. Podemos usar la función np.percentile() para calcular este intervalo del 90% de la siguiente manera:

np.percentile(null_outcomes, [5,95])

Salida

[39. 61.]

Calcular un valor P unilateral

Los cálculos e interpretaciones del valor P dependen de la hipótesis alternativa de una prueba, una descripción de la diferencia con la expectativa que nos interesa. Para estimar el valor p para una prueba de hipótesis binomial con las siguientes hipótesis nulas y alternativas:

• Nulo: la probabilidad de compra era del 10%
• Alternativa: la probabilidad de una tasa de compra fue MENOS DEL 10%

Esta prueba de hipótesis plantea la pregunta: SI la probabilidad de la probabilidad de compra era del 10%, ¿cuál es la probabilidad de observar menos?

null_outcomes = np.array(null_outcomes)
p_value = np.sum(null_outcomes <= 41)/len(null_outcomes) 
print(p_value)

Salida

0.1031

Calcular un valor P bilateral

En el ejercicio anterior, calculamos un valor \(p\) unilateral. En este ejercicio, estimaremos un valor \(p\) para una prueba bilateral, que es la configuración predeterminada para muchas funciones en Python (y otros lenguajes, como R!).

Supongamos que la verdadera probabilidad de compra era del 10%. ¿Cuál es la probabilidad de observar menos o mas compras?.

null_outcomes = np.array(null_outcomes)
p_value = np.sum((null_outcomes <= 41) | (null_outcomes >= 59)) /len(null_outcomes) 
print(p_value)

salida

0.2059

Escribir una función de prueba binomial

Hasta ahora, hemos realizado una prueba de hipótesis binomial simulada para Live-it-LIVE.com. En este ejercicio, usaremos nuestro código de los ejercicios anteriores para escribir nuestra propia función de prueba binomial. Nuestra función utilizará simulación, por lo que estimará (aunque con bastante precisión) los mismos valores p que obtendríamos usando ecuaciones matemáticas mucho más complejas.

Se ha descrito una función en script.py que contiene el código que utilizamos para Live_it_LIVE dentro de una función denominada simulation_binomial_test(). Su objetivo en los próximos ejercicios será editar esta función para que admita los valores de lo siguiente:

• La estadística de muestra observada (p. ej., 41 compras)
• El tamaño de la muestra (p. ej., 500 visitantes)
• La probabilidad nula de éxito (por ejemplo, 0,10 de probabilidad de una compra)
• La función debe devolver un valor p para una prueba unilateral donde la hipótesis alternativa es que la verdadera probabilidad de éxito es MENOR QUE la nula.

def simulation_binomial_test(observed_successes, n, p):
  #initialize null_outcomes
  null_outcomes = []
  
  #generate the simulated null distribution
  for i in range(10000):
    simulated_monthly_visitors = np.random.choice(['y', 'n'], n, p)
    num_purchased = np.sum(simulated_monthly_visitors == 'y')
    null_outcomes.append(num_purchased)

  #calculate a 1-sided p-value
  null_outcomes = np.array(null_outcomes)
  p_value = np.sum(null_outcomes <= observed_successes)/len(null_outcomes) 
  
  #return the p-value
  return p_value

Testing

p_value1 = simulation_binomial_test(41, 500, .1)
print("simulation p-value: ", p_value1)

Salida

0,2667

De todo lo visto anteriormente la funcion binom_test() de SciPy realiza el mismo calculo:

from scipy.stats import binom_test

p_value2 = binom_test(45, 500, .1, alternative = 'less')
print("binom_test p-value: ", p_value2)

Salida

0,25468926056232155

Prueba binomial con SciPy

Hasta ahora, hemos realizado una prueba de hipótesis binomial simulada para Live-it-LIVE.com. En este apartado, usaremos nuestro código de los ejercicios anteriores para escribir nuestra propia función de prueba binomial. Nuestra función utilizará simulación, por lo que estimará (aunque con bastante precisión) los mismos valores \(p\) que obtendríamos usando ecuaciones matemáticas mucho más complejas.

Más formalmente, la distribución binomial describe el número de “éxitos” esperados en un experimento con cierto número de “ensayos”. En el ejemplo que acaba de analizar, el experimento consistió en que 500 personas visitaran Live-it-LIVE.com. Para cada una de esas pruebas (visitantes), esperábamos un 10% de posibilidades de compra (éxito), pero observamos sólo 41 éxitos (menos del 10%).

SciPy tiene una función llamada binom_test(), que realiza una prueba binomial. La hipótesis alternativa predeterminada para la función binom_test() es bilateral, pero esto se puede cambiar usando el parámetro alternative (por ejemplo, alternative = 'less'ejecutará una prueba de cola inferior unilateral).

binom_test() requiere tres datos de entrada: el número de éxitos observados, el número total de ensayos y la probabilidad esperada de éxito. Por ejemplo, con 10 lanzamientos de una moneda justa (pruebas), la probabilidad esperada de que salga cara es 0,5.

Ejecutar la prueba binomial bilateral para determinar si las 41 compras observadas entre 500 visitantes de Live-it-LIVE.com están lo suficientemente alejadas de la tasa de compra esperada del 10% para convencerlo de que el ritmo de compra fue diferente al esperado esta semana.

from scipy import binom_test
p_value_2sided = binom_test(41, n=500, p=0.1)
print(p_value_2sided) 

Salidaç

0.20456397700678308

La misma prueba de hipótesis que en el paso 1, pero ahora como una prueba unilateral donde la hipótesis alternativa es que la probabilidad de que un visitante realice una compra fue inferior al 10% (0,1).

from scipy import binom_test
p_value_1sided = binom_test(41, n=500, p=0.1, alternative = 'less')
print(p_value_1sided) 

Salida

0.1001135269756488

Resumen

Ahora sabes cómo ejecutar una prueba de hipótesis binomial usando una función SciPy, ¡o simulándola tú mismo! Esto le resultará muy útil como científico de datos porque le permitirá investigar qué sucede si las funciones escritas previamente arrojan resultados sorprendentes. Ahora también tiene una comprensión conceptual de cómo funciona una prueba binomial y qué preguntas pretende responder. En resumen, estas son algunas de las cosas que ha aprendido sobre las pruebas de hipótesis en general:

• Todas las pruebas de hipótesis comienzan con una hipótesis nula y alternativa.
• Los resultados de una prueba de hipótesis que podrían informarse incluyen:
  • intervalos de confianza
  • valores p
• Una prueba de hipótesis se puede simular mediante:
  • tomar muestras aleatorias repetidas donde se supone que la hipótesis nula es verdadera
  • usar esas muestras simuladas para generar una distribución nula
  • comparar una estadística de muestra observada con esa distribución nula

Introducción a los umbrales de significancia

A veces, cuando ejecutamos una prueba de hipótesis, simplemente informamos un valor p o un intervalo de confianza y damos una interpretación (por ejemplo, el valor \(p\) fue 0,05, lo que significa que hay un 5 % de probabilidad de observar dos o menos cabezas). en 10 lanzamientos de moneda).

En otras situaciones, queremos usar nuestro valor p para tomar una decisión o responder una pregunta de sí o no. Por ejemplo, supongamos que estamos desarrollando una nueva pregunta de prueba en Codecademy y queremos que los alumnos tengan un 70 % de posibilidades de responder correctamente la pregunta (más alto significaría que la pregunta es demasiado fácil, más bajo significaría que la pregunta es demasiado difícil). Mostramos nuestra pregunta del cuestionario a una muestra de 100 alumnos y 60 de ellos responden correctamente. ¿Es esto significativamente diferente de nuestro objetivo del 70%? Si es así, queremos eliminar la pregunta e intentar reescribirla.

Para convertir un valor \(p\), que es una probabilidad, en una respuesta de sí o no, los científicos de datos suelen utilizar un umbral de significancia preestablecido. El umbral de significancia puede ser cualquier número entre 0 y 1, pero una opción común es 0,05. Los valores de \(p\) que son inferiores a este umbral se consideran “significativos”, mientras que los valores de \(p\) mayores se consideran “no significativos”.

Realizamos una prueba de hipótesis binomial con las siguientes hipótesis nula y alternativa:

• Nulo: la probabilidad de que un alumno responda correctamente la pregunta es del 70%.
• Alternativa: La probabilidad de que un alumno responda correctamente la pregunta no es del 70%.

Suponiendo que establecimos un umbral de significancia de 0,05 para esta prueba:

• Si el valor \(p\) es inferior a 0,05, el valor p es significativo. “Rechazaremos la hipótesis nula” y concluiremos que la probabilidad de una respuesta correcta es significativamente diferente del 70%. Esto nos llevaría a reescribir la pregunta.
• Si el valor \(p\) es mayor que 0,05, el valor p no es significativo. No podremos rechazar la hipótesis nula y concluiremos que la probabilidad de una respuesta correcta no es significativamente diferente del 70%. Esto nos llevaría a dejar la pregunta en el sitio.

Tipos de errores

Siempre que ejecutamos una prueba de hipótesis utilizando un umbral de significancia, nos exponemos a cometer dos tipos diferentes de errores: errores tipo I (falsos positivos) y errores tipo II (falsos negativos):

Resultado / Verdad	Hipótesis nula: es verdad	Hipótesis nula: es falsa
Valor p significativo	Error tipo I	¡Correcto!
Valor p no significativo	¡Correcto!	Error tipo II

Considere la prueba de hipótesis de preguntas del cuestionario descrita en los ejercicios anteriores:

• Nulo: la probabilidad de que un alumno responda correctamente una pregunta es del 70%.
• Alternativa: La probabilidad de que un alumno responda correctamente una pregunta no es del 70%.

Supongamos, por un momento, que la probabilidad real de que un alumno responda correctamente la pregunta es del 70% (si mostráramos la pregunta a TODOS los alumnos, exactamente el 70% la respondería correctamente). Esto nos coloca en la primera columna de la tabla anterior (la hipótesis nula “es verdadera”). Si ejecutamos una prueba y calculamos un valor p significativo, cometeremos un error tipo I (también llamado falso positivo porque el valor p es falsamente significativo), lo que nos llevará a eliminar la pregunta cuando no sea necesario.

Por otro lado, si la probabilidad real de acertar la pregunta no es del 70%, la hipótesis nula “es falsa” (la columna más a la derecha de nuestra tabla). Si ejecutamos una prueba y calculamos un valor p no significativo, cometemos un error de tipo II, lo que nos lleva a dejar la pregunta en nuestro sitio cuando deberíamos haberla eliminado.

Configuración de la tasa de error tipo I

Resulta que, cuando ejecutamos una prueba de hipótesis con un umbral de significancia, el umbral de significancia es igual a la tasa de error tipo I (falso positivo) de la prueba. Para ver esto, podemos usar una simulación.

Recuerde nuestro ejemplo de pregunta del cuestionario: la hipótesis nula es que la probabilidad de acertar una pregunta del cuestionario es igual al 70%. Cometeremos un error de tipo I si la hipótesis nula es correcta (la probabilidad real de una respuesta correcta es del 70%), pero de todos modos obtenemos un valor p significativo.

Problemas con pruebas de hipótesis múltiples

Si bien los umbrales de significancia permiten a un científico de datos controlar la tasa de falsos positivos para una sola prueba de hipótesis, esto comienza a fallar cuando se realizan múltiples pruebas como parte de un solo estudio.

Por ejemplo, supongamos que estamos escribiendo un cuestionario en codecademy que incluirá 10 preguntas. Para cada pregunta, queremos saber si la probabilidad de que un alumno responda correctamente la pregunta es diferente del 70%. Ahora tenemos que ejecutar 10 pruebas de hipótesis, una para cada pregunta.

Si la hipótesis nula es verdadera para cada prueba de hipótesis (la probabilidad de una respuesta correcta es del 70% para cada pregunta) y utilizamos un nivel de significancia de 0,05 para cada prueba, entonces:

• Cuando ejecutamos una prueba de hipótesis para una sola pregunta, tenemos un 95% de posibilidades de obtener la respuesta correcta (un valor p > 0,05) y un 5% de posibilidades de cometer un error de tipo I.

• Cuando ejecutamos pruebas de hipótesis para dos preguntas, tenemos solo un 90% de posibilidades de obtener la respuesta correcta para ambas pruebas de hipótesis (0,95*0,95 = 0,90) y un 10% de posibilidades de cometer al menos un error de tipo I.

• Cuando realizamos pruebas de hipótesis para las 10 preguntas, tenemos un 60 % de posibilidades de obtener la respuesta correcta para las diez pruebas de hipótesis (0,95 ^ 10 = 0,60) y un 40 % de posibilidades de cometer al menos un error de tipo I.

Cuando se ejecuta más de una prueba de hipótesis con un umbral de significancia particular, la probabilidad de cometer al menos un error tipo I es:

Para abordar este problema, es importante planificar la investigación con anticipación: decida qué preguntas desea abordar y determine cuántas pruebas de hipótesis necesita realizar. Cuando ejecute varias pruebas, utilice un umbral de significancia más bajo (p. ej., 0,01) para cada prueba para reducir la probabilidad de cometer un error de tipo I.

Cuando se ejecutan múltiples pruebas de hipótesis utilizando el mismo conjunto de datos y un umbral de significancia fijo (como el comúnmente usado ( \alpha = 0.05 )), la probabilidad de cometer al menos un error tipo I —es decir, rechazar incorrectamente la hipótesis nula cuando es verdadera— en alguna de las pruebas aumenta con cada prueba adicional realizada.

Esta situación se debe a lo que se conoce como el problema de la comparación múltiple o multiplicidad. La forma más sencilla de entender esto es mediante la idea de que cada prueba tiene una probabilidad (\alpha) de producir un error tipo I si la hipótesis nula es cierta. Cuando se hacen múltiples pruebas, estas probabilidades no desaparecen, sino que se acumulan.

Por lo tanto, la respuesta correcta es:

superior al umbral de significancia

Para mitigar este efecto y controlar la probabilidad de cometer uno o más errores de Tipo I cuando se realizan múltiples pruebas, los investigadores pueden ajustar el nivel de significancia utilizando métodos como el ajuste de Bonferroni o el procedimiento de control de la tasa de falsos descubrimientos (FDR). Estos métodos buscan proporcionar un equilibrio más preciso entre el riesgo de cometer errores tipo I y la capacidad de detectar verdaderos efectos estadísticamente significativos.

Ejercicios: Supongamos que un grupo de investigadores está interesado en saber si los residentes de una ciudad en particular tienden a tener presión arterial sistólica (PAS) alta en promedio. Toman una muestra de 100 residentes, miden su PAS y quieren realizar una prueba de hipótesis para comprender si la PAS promedio de todos los residentes es significativamente superior a 120 mm Hg. ¿Qué tipo de prueba de hipótesis sería apropiada para esta pregunta?

Opciones de respuesta:

• Prueba t de una muestra
• Prueba t de dos muestras
• Prueba de chi-cuadrado
• prueba binomial

Supongamos que una empresa de medios en línea envió recientemente un correo electrónico a 100 suscriptores potenciales, promocionando su nuevo boletín. Antes de enviar el correo electrónico a aún más suscriptores potenciales, la empresa quiere asegurarse de que estén cumpliendo su objetivo: que el 50% (o más) de los destinatarios del correo electrónico abran el correo electrónico. ¿Qué tipo de prueba de hipótesis sería apropiada para esta pregunta?

Opciones de respuesta

• prueba Z
• Prueba t de una muestra
• Prueba de chi-cuadrado
• prueba binomial