Analisis Multivariado

El análisis multivariado es el análisis de tres o más variables. Esto nos permite observar las correlaciones (es decir, cómo cambia una variable con respecto a otra) e intentar hacer predicciones para el comportamiento futuro con mayor precisión que con el análisis bivariado.

Notebook: Discussing multivariate analysis using the Titanic dataset

Inicialmente, exploramos la visualización del análisis univariado y bivariado; Asimismo, visualicemos el concepto de análisis multivariado.

Una forma común de representar datos multivariados es hacer un diagrama de dispersión matricial, conocido como diagrama de pares. Un gráfico matricial o un gráfico de pares muestra cada par de variables comparadas entre sí. El gráfico de pares nos permite ver tanto la distribución de variables individuales como las relaciones entre dos variables:

Podemos usar lafunción scatter_matrix() del paquete pandas.tools.plotting o la función seaborn.pairplot() del paquete seaborn para hacer esto:

# pair plot with plot type regression
sns.pairplot(df,vars = ['normalized-losses', 'price','horsepower'], kind="reg")
plt.show()

Este código trazará una matriz de 3 x 3 de diferentes gráficos para los datos en las columnas de pérdidas normalizadas, precio y caballos de fuerza:

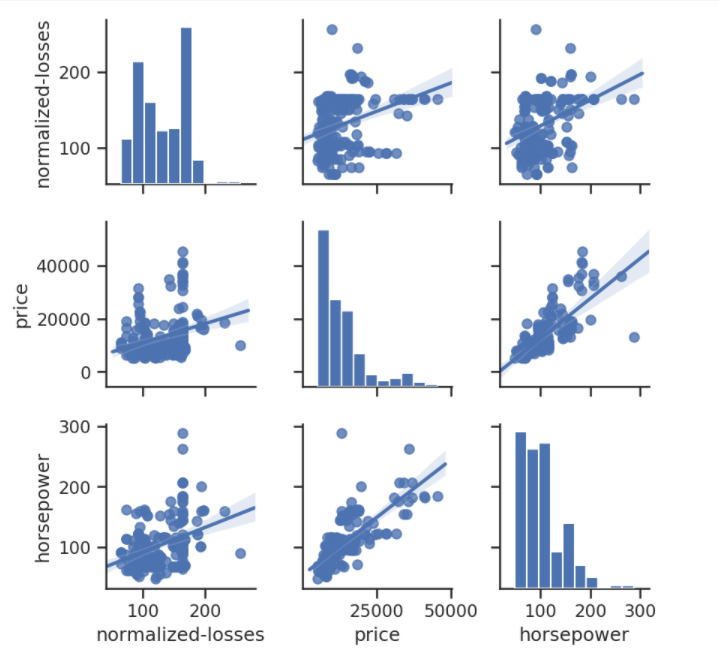
Como se muestra en el diagrama anterior, el histograma en diagonal nos permite ilustrar la distribución de una sola variable. Los gráficos de regresión en los triángulos superior e inferior demuestran la relación entre dos variables. El gráfico del medio en la primera fila muestra el gráfico de regresión; esto representa que no existe correlación entre las pérdidas normalizadas y el precio de los automóviles. En comparación, el gráfico de regresión del medio en la fila inferior ilustra que existe una enorme correlación entre el precio y los caballos de fuerza.

De manera similar, podemos realizar un análisis multivariado utilizando un gráfico de pares especificando los colores, las etiquetas, el tipo de gráfico, el tipo de gráfico diagonal y las variables. Entonces, hagamos otro diagrama de pares:

#pair plot (matrix scatterplot) of few columns 
sns.set(style="ticks", color_codes=True)
sns.pairplot(df,vars = ['symboling', 'normalized-losses','wheel-base'], hue="drive-wheels")
plt.show()

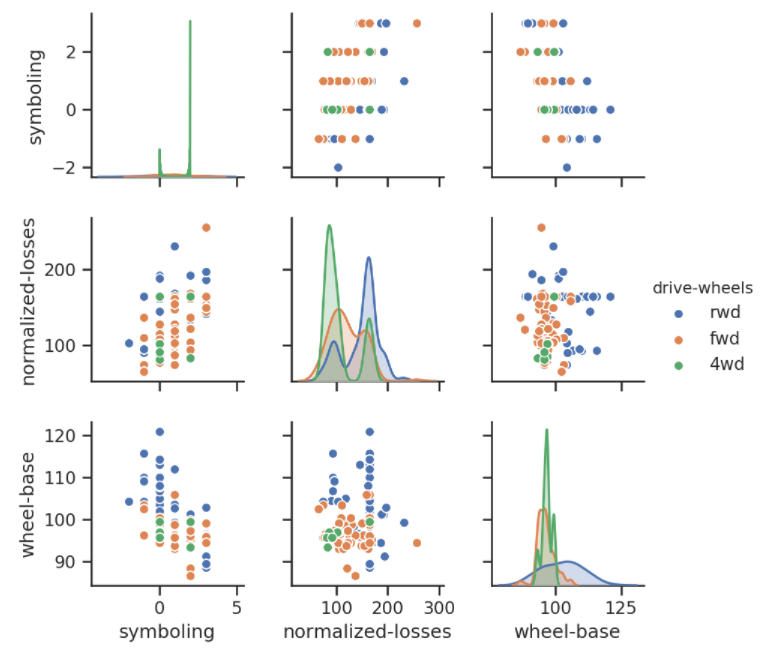
Este es un gráfico de pares de registros de las columnas de simbolización, pérdidas normalizadas, distancia entre ejes y ruedas motrices.

Los gráficos de densidad en la diagonal nos permiten ver la distribución de una sola variable, mientras que los diagramas de dispersión en los triángulos superior e inferior muestran la relación (o correlación) entre dos variables. El parámetro de tono es el nombre de la columna utilizada para las etiquetas de los puntos de datos; En este diagrama, el tipo de ruedas motrices está etiquetado por color. El gráfico situado más a la izquierda en la segunda fila muestra el gráfico de dispersión de las pérdidas normalizadas frente a la distancia entre ejes.

Como se analizó anteriormente, el análisis de correlación es una técnica eficaz para descubrir si alguna de las variables en un conjunto de datos multivariado está correlacionada.

Para calcular el coeficiente de correlación lineal (Pearson) para un par de variables, podemos usar la función dataframe.corr(method ='pearson') del paquete pandas y la función pearsonr() del paquete scipy.stats:

from scipy import stats
corr = stats.pearsonr(df["price"], df["horsepower"])
print("p-value:\t", corr[1])
print("cor:\t\t", corr[0])

Output

p-value: 6.369057428260101e-48 
cor: 0.8095745670036559

Aquí, la correlación entre estas dos variables es 0.80957, que está cerca de +1. Por lo tanto, podemos asegurarnos de que tanto el precio como la potencia tienen una correlación muy positiva.

Usando la función corr() de pandas, la correlación entre todo el registro numérico se puede calcular de la siguiente manera:

# numeric_only selecciona solo las variables float, int or boolean del dataframe. 
correlation = df.corr(method='pearson', numeric_only = True)
correlation

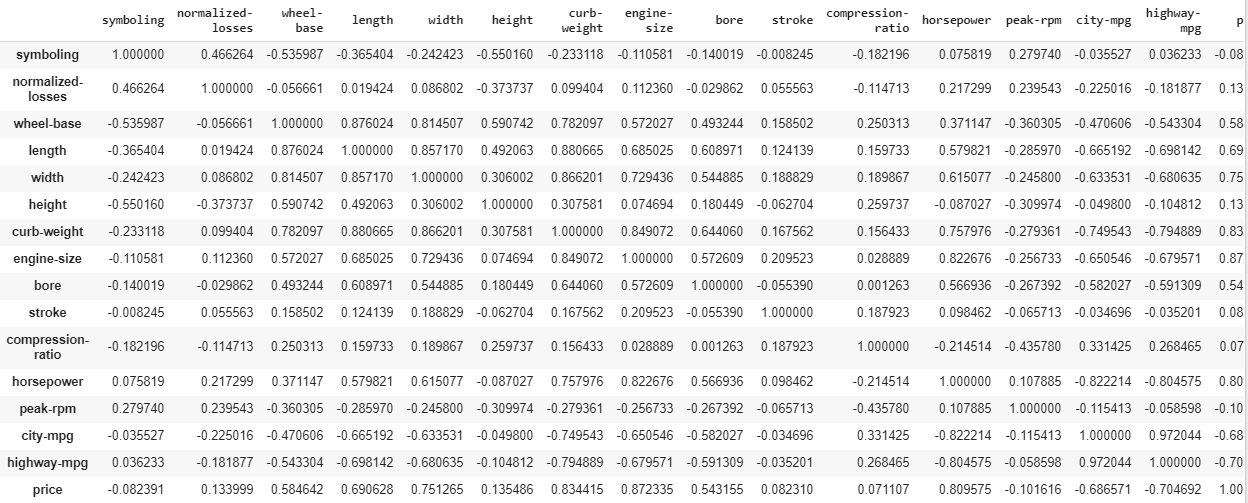
El resultado de este código se proporciona de la siguiente manera :

Ahora, visualicemos este análisis de correlación usando un mapa de calor. Un mapa de calor es la mejor técnica para hacer que esto se vea hermoso y más fácil de interpretar:

sns.heatmap(correlation,xticklabels=correlation.columns,
            yticklabels=correlation.columns)

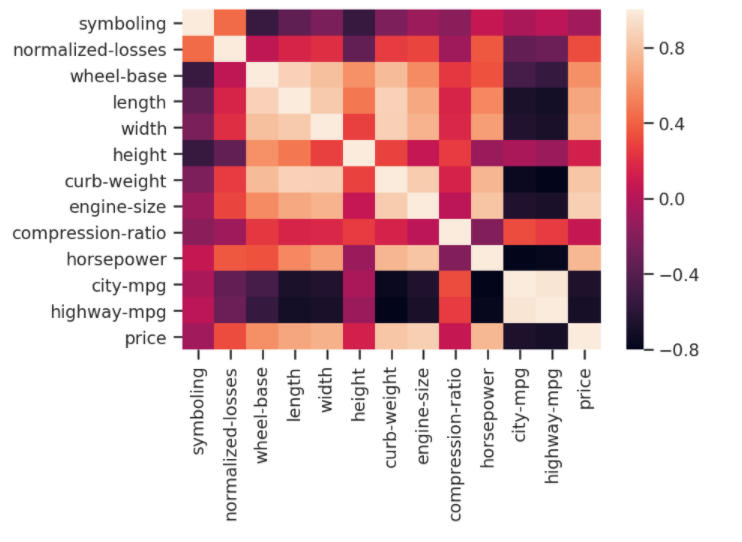
Un coeficiente cercano a 1 significa que existe una correlación positiva muy fuerte entre las dos variables. La línea diagonal es la correlación de las variables entre sí mismas, por lo que, por supuesto, serán 1.