EDA avanzada

La exploración es genial, pero la exploración con un mapa es aún mejor. Esta unidad proporciona un mapa para comenzar.

¿Qué cubrirá el análisis de datos exploratorios avanzados?

• Calcular la varianza de una variable (se pretende redundancia)
• Evaluar la distribución
• Informe sobre cuartiles, cuantiles y rango intercuartil
• Explorar datos categóricos
• Transforme los datos para satisfacer sus necesidades.

Variance

Encontrar la media, la mediana y la moda de un conjunto de datos es una buena manera de comenzar a comprender la forma general de sus datos.

Sin embargo, esas tres estadísticas descriptivas sólo cuentan una parte de la historia. Considere los dos conjuntos de datos siguientes:

dataset_one = [-4, -2, 0, 2, 4]
dataset_two = [-400, -200, 0, 200, 400]

Estos dos conjuntos de datos tienen la misma media y mediana; resulta que ambos valores son 0. Si solo reportáramos estas dos estadísticas, no estaríamos comunicando ninguna diferencia significativa entre estos dos conjuntos de datos.

Aquí es donde entra en juego la variación . La varianza es una estadística descriptiva que describe qué tan dispersos están los puntos en un conjunto de datos.

Distancia desde la media

¿Cómo intentaría capturar la distribución de los datos en un solo número?

Comencemos con nuestra intuición: queremos que la varianza de un conjunto de datos sea un número grande si los datos están dispersos y un número pequeño si los datos están muy juntos.

Mucha gente puede considerar inicialmente utilizar el rango de datos. Pero eso sólo considera dos puntos en todo su conjunto de datos. En cambio, podemos incluir cada punto en nuestro cálculo encontrando la diferencia entre cada punto de datos y la media.

Si los datos están muy juntos, entonces cada punto de datos tenderá a estar cerca de la media y la diferencia será pequeña. Si los datos están dispersos, la diferencia entre cada punto de datos y la media será mayor.

Matemáticamente, podemos escribir esta comparación como

\[diferencia=X−µ\]

¿Dónde X hay un único punto de datos y la letra griega ‘µ’ la media?

Distancias promedio

Ahora tenemos cinco valores diferentes que describen qué tan lejos está cada punto de la media. Este parece ser un buen comienzo para describir la difusión de los datos. Pero el objetivo de calcular la varianza era obtener un número que describiera el conjunto de datos. No queremos informar cinco valores; queremos combinarlos en una estadística descriptiva.

Para ello, tomaremos el promedio de esos cinco números. Al sumar esos números y dividirlos por 5, terminaremos con un solo número que describe la distancia promedio entre nuestros puntos de datos y la media.

Tenga en cuenta que aún no hemos terminado : nuestra respuesta final parecerá un poco extraña aquí. Hay un pequeño problema que solucionaremos en el siguiente ejercicio.

Cuadrar las diferencias

¡Casi estámos allí! Tenemos un pequeño problema con nuestra ecuación. Considere este conjunto de datos muy pequeño:

[-5, 5]

La media de este conjunto de datos es 0, por lo que cuando encontramos la diferencia entre cada punto y la media obtenemos -5 - 0 = -5y 5 - 0 = 5.

Cuando tomamos el promedio de -5y 5para obtener la varianza, obtenemos 0!

Ahora piense en lo que sucedería si el conjunto de datos fuera [-200, 200]. ¡Obtendríamos el mismo resultado! Eso no puede ser correcto: el conjunto de datos con 200está mucho más disperso que el conjunto de datos con 5, por lo que la variación debería ser mucho mayor.

El problema aquí son los números negativos. Debido a que uno de nuestros puntos de datos estaba 5unidades por debajo de la media y el otro estaba 5unidades por encima de la media, ¡se cancelaron entre sí!

Al calcular la varianza, no nos importa si un punto de datos estaba por encima o por debajo de la media; lo único que nos importa es qué tan lejos estaba. Para deshacernos de esos molestos números negativos, elevaremos al cuadrado la diferencia entre cada punto de datos y la media.

Nuestra ecuación para encontrar la diferencia entre un punto de datos y la media ahora se ve así:

\[diferencia=( X−µ )^2\]

Variaza en NumPy

¡Bien hecho! Ha calculado la varianza de un conjunto de datos. Analicemos un poco esta ecuación.

• La varianza suele estar representada por el símbolo sigma al cuadrado.
• Comenzamos tomando cada punto del conjunto de datos (de un número de punto 1a otro N) y encontrando la diferencia entre ese punto y la media.
• A continuación, elevamos al cuadrado cada diferencia para que todas las diferencias sean positivas.
• Finalmente, promediamos esas diferencias al cuadrado sumándolas y dividiéndolas por N, el número total de puntos en el conjunto de datos.

Todo este trabajo se puede realizar rápidamente utilizando la biblioteca NumPy de Python. La función var() toma una lista de números como parámetro y devuelve la varianza de ese conjunto de datos.

import numpy as np

dataset = [3, 5, -2, 49, 10]
variance = np.var(dataset)

Desviación Estándar

La varianza es una estadística difícil de usar porque sus unidades son diferentes tanto de la media como de los datos mismos. Por ejemplo, la media de nuestro conjunto de datos de la NBA es 77.98pulgadas. Debido a esto, podemos decir que alguien que mide 80pulgadas de alto es aproximadamente dos pulgadas más alto que el jugador promedio de la NBA.

Sin embargo, debido a que la fórmula de la varianza incluye elevar al cuadrado la diferencia entre los datos y la media, la varianza se mide en unidades al cuadrado . Esto significa que la varianza de nuestro conjunto de datos de la NBA es 13.32pulgadas al cuadrado.

Este resultado es difícil de interpretar en contexto con la media o los datos porque sus unidades son diferentes. Aquí es donde resulta útil la desviación estándar estadística.

La desviación estándar se calcula tomando la raíz cuadrada de la varianza. sigmaes el símbolo comúnmente utilizado para la desviación estándar.

En Python, puedes sacar la raíz cuadrada de un número usando ** 0.5:

num = 25
num_square_root = num ** 0.5

Desviación estándar en NumPy

1 minuto Hay una función NumPy dedicada a encontrar la desviación estándar de un conjunto de datos; podemos eliminar el paso de encontrar primero la varianza. La función NumPy std() toma un conjunto de datos como parámetro y devuelve la desviación estándar de ese conjunto de datos:

import numpy as np

dataset = [4, 8, 15, 16, 23, 42]
standard_deviation = np.std(dataset)

Usando la desviación estándar

Ahora que podemos calcular la desviación estándar de un conjunto de datos, ¿qué podemos hacer con él?

Ahora que nuestras unidades coinciden, nuestra medida de dispersión es más fácil de interpretar. Al encontrar el número de desviaciones estándar que un punto de datos está alejado de la media, podemos comenzar a investigar qué tan inusual es realmente ese punto de datos. De hecho, normalmente se puede esperar que alrededor del 68 % de los datos se encuentren dentro de una desviación estándar de la media, el 95 % de los datos se encuentren dentro de dos desviaciones estándar de la media y el 99,7 % de los datos se encuentren dentro de tres desviaciones estándar. de la media.

Si tiene un punto de datos que está a más de tres desviaciones estándar de la media, ¡es un dato increíblemente inusual!

Describir un Histograma

Media y Mediana

Una de las formas más comunes de resumir un conjunto de datos es comunicar su centro. La siguiente figura muestra las edades promedio y mediana de un conjunto de datos de 100 autores. Como era de esperar, los valores promedio y mediana están cerca del centro de la distribución.

Spread

Una vez que haya encontrado el centro de sus datos, puede pasar a identificar los extremos de su conjunto de datos: los valores mínimo y máximo. Estos valores, tomados con la media y la mediana, comienzan a indicar la forma del conjunto de datos subyacente.

Skew (sesgo)

Una vez que tenga el centro y el rango de sus datos, puede comenzar a describir su forma. La asimetría de un conjunto de datos es una descripción de la simetría de los datos.

• Un conjunto de datos con un pico prominente y colas similares a la izquierda y a la derecha se denomina simétrico. La mediana y la media de un conjunto de datos simétrico son similares.

• Un histograma con una cola que se extiende hacia la derecha se denomina conjunto de datos sesgado a la derecha. La mediana de este conjunto de datos es menor que la media.

• Un histograma con un pico prominente a la derecha y una cola que se extiende hacia la izquierda se denomina conjunto de datos sesgado hacia la izquierda. La mediana de este conjunto de datos es mayor que la media.

Modalidad

La modalidad describe el número de picos en un conjunto de datos. Hasta ahora, solo hemos analizado conjuntos de datos con un pico distinto, conocido como unimodal, este es el más común.

• Un conjunto de datos bimodal tiene dos picos distintos.
• Un conjunto de datos multimodal tiene más de dos picos. El siguiente histograma muestra tres picos.
• También es posible que vea conjuntos de datos sin una agrupación obvia. Conjuntos de datos como estos se denominan distribuciones uniformes

Outliers

Un valor atípico es un punto de datos que está lejos del resto del conjunto de datos. Los valores atípicos no tienen una definición formal, pero son fáciles de determinar mirando el histograma. El siguiente histograma muestra un ejemplo de un valor atípico. Hay un punto de datos que es mucho más grande que el resto.

Si ve un valor atípico en su conjunto de datos, vale la pena informarlo e investigarlo. Estos datos a menudo pueden indicar un error en sus datos o una idea interesante.

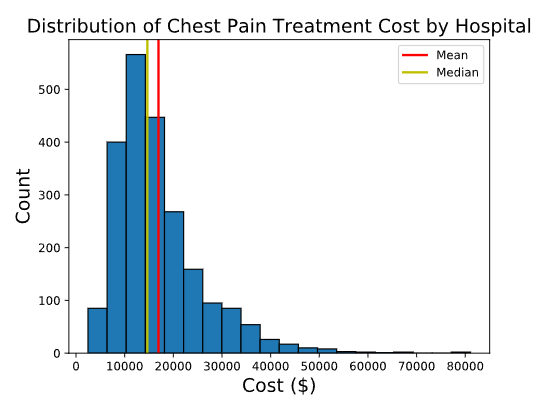
Este histograma muestra la distribución del costo del dolor torácico en más de 2,000 hospitales en los Estados Unidos. Los costos promedio y mediano son $16,948 y $14,659.6, respectivamente. Dado que los datos son unimodales, con un máximo local y una asimetría a la derecha, el hecho de que el promedio sea mayor que la mediana coincide con nuestras expectativas.

El rango de costos es muy amplio, $78,624, con el costo más bajo de $2,459 y el costo más alto de $81,083. Hay un hospital, Bayonne Hospital Center, que cobra mucho más que el resto, con un costo de $81,083.

Quartiles

Una forma común de comunicar una descripción general de alto nivel de un conjunto de datos es encontrar los valores que dividen los datos en cuatro grupos de igual tamaño.

Al hacer esto, podemos decir si un nuevo punto de datos se encuentra en el primer, segundo, tercer o cuarto trimestre de los datos.

Los valores que dividen los datos en cuartos son los cuartiles .

Esos valores se denominan primer cuartil (Q1), segundo cuartil (Q2) y tercer cuartil (Q3).

En la imagen de arriba, Q1 es 10, Q2 es 13y Q3 es 22. Esos tres valores dividen los datos en cuatro grupos, cada uno de los cuales contiene cinco puntos de datos.

El segundo cuartil

Encontrar el segundo cuartil (Q2). Q2 resulta ser exactamente la mediana . La mitad de los datos caen por debajo del segundo trimestre y la otra mitad de los datos caen por encima del segundo trimestre.

El primer paso para encontrar los cuartiles de un conjunto de datos es ordenar los datos de menor a mayor. Por ejemplo, a continuación se muestra un conjunto de datos sin clasificar:

[ 8 ,15 ,​4 ,− 108 ,dieciséis ,​23 ,42 ]

# Después de ordenar el conjunto de datos, se ve así:

[ - 108 ,4 ,8 ,15 ,​dieciséis ,​23 ,42 ]

Ahora que la lista está ordenada, podemos encontrar Q2. En el conjunto de datos de ejemplo anterior, Q2 (y la mediana) es 15: hay tres puntos debajo 15y tres puntos arriba 15.

Número par de puntos de datos

Quizás se pregunte qué sucede si hay un número par de puntos en el conjunto de datos. Por ejemplo, si eliminamos -108de nuestro conjunto de datos, ahora se verá así:

[ 4 ,8 ,15 ,​dieciséis ,​2 3 ,4 2 ]

El segundo trimestre se sitúa ahora entre 15 y 16. Hay un par de estrategias diferentes que puede utilizar para calcular Q2 en esta situación. Una de las formas más comunes es tomar el promedio de esos dos números. En este caso, eso sería 15.5.

Recuerda que puedes encontrar el promedio de dos números sumándolos y dividiéndolos por dos.

Q1 y Q3

Ahora que hemos encontrado Q2, podemos usar ese valor para ayudarnos a encontrar Q1 y Q3. Recuerde nuestro conjunto de datos de demostración:

[ - 108 ,4 ,8 ,15 , 16 ,​23 ,42 ]

En este ejemplo, Q2 es 15. Para encontrar Q1, tomamos todos los puntos de datos más pequeños que Q2 y encontramos la mediana de esos puntos. En este caso, los puntos menores que Q2 son:

[ - 108 ,4 ,8 ]

La mediana de ese conjunto de datos más pequeño es 4. ¡Eso es el primer trimestre!

Para encontrar Q3, haz el mismo proceso usando los puntos que son mayores que Q2. Tenemos los siguientes puntos:

[ dieciséis ,​2 3 ,4 2 ]

La mediana de esos puntos es 23. ¡Eso es el tercer trimestre! Ahora tenemos tres puntos que dividen el conjunto de datos original en grupos de cuatro tamaños iguales.

Método dos: incluir Q2

Acaba de aprender un método comúnmente utilizado para calcular los cuartiles de un conjunto de datos. Sin embargo, existe otro método igualmente aceptado que da como resultado valores diferentes.

Tenga en cuenta que no existe un método universalmente acordado para calcular los cuartiles y, como resultado, dos herramientas diferentes pueden arrojar resultados diferentes.

El segundo método incluye Q2 al intentar calcular Q1 y Q3. Echemos un vistazo a un ejemplo:

[ - 108 ,4 ,8 ,15 ,16 ,​23 ,42 ]

Usando el primer método, encontramos que Q1 es 4. Al observar todos los puntos por debajo del segundo trimestre, excluimos el segundo trimestre. Usando este segundo método, incluimos Q2 en cada mitad.

Por ejemplo, al calcular el primer trimestre utilizando este nuevo método, ahora encontraríamos la mediana de este conjunto de datos:

[ - 108 ,4 ,8 ,15 ]​

Usando este método, Q1 es 6.

Cuantiles

Los cuantiles son puntos que dividen un conjunto de datos en grupos de igual tamaño. Por ejemplo, digamos que acabas de realizar un examen y quieres saber si estás en el 10% superior de la clase. Una forma de determinar esto sería dividir los datos en diez grupos con el mismo número de puntos de datos en cada grupo y ver en qué grupo se encuentra.

Treinta grados de estudiantes se dividieron en diez grupos de tres. Hay nueve valores que dividen el conjunto de datos en diez grupos de igual tamaño; cada grupo tiene 3 puntuaciones de pruebas diferentes.

¡Esos nueve valores que dividen los datos son cuantiles! Específicamente, son los 10 cuantiles o deciles.

Puedes encontrar cualquier número de cuantiles. Por ejemplo, si divide el conjunto de datos en 100 grupos de igual tamaño, los 99 valores que dividen los datos son los 100 cuantiles o percentiles.

Los cuartiles son algunos de los cuantiles más utilizados. Los cuartiles dividen los datos en cuatro grupos de igual tamaño.

En esta lección, le mostraremos cómo calcular cuantiles usando NumPy y analizaremos algunos de los cuantiles más utilizados.

Cuantiles en NumPy

La biblioteca NumPy tiene una función llamada quantile() que calculará rápidamente los cuantiles de un conjunto de datos.

quantile() toma dos parámetros. El primero es el conjunto de datos que está utilizando. El segundo parámetro es un número único o una lista de números entre 0y 1. Estos números representan los lugares de los datos donde desea dividir.

Por ejemplo, si solo desea el valor que divide el primer 10% de los datos del 90% restante, puede usar este código:

import numpy as np

dataset = [5, 10, -20, 42, -9, 10]
ten_percent = np.quantile(dataset, 0.10)

ten_percent ahora tiene el valor -14.5. Este resultado técnicamente no es un cuantil, porque no divide el conjunto de datos en grupos de tamaños iguales; este valor divide los datos en un grupo con el 10 % de los datos y otro con el 90 %.

Sin embargo, aún sería útil si tuviera curiosidad sobre si un punto de datos se encuentra en el 10% inferior del conjunto de datos.

Muchos cuantiles

En el último ejercicio, encontramos un único “cuantil”: dividimos el primer 23% de los datos del 77% restante.

Sin embargo, los cuantiles suelen ser un conjunto de valores que dividen los datos en grupos de igual tamaño. Por ejemplo, si desea obtener los 5 cuantiles, o los cuatro valores que dividen los datos en cinco grupos de igual tamaño, puede usar este código:

import numpy as np

dataset = [5, 10, -20, 42, -9, 10]
ten_percent = np.quantile(dataset, [0.2, 0.4, 0.6, 0.8])

Tenga en cuenta que tuvimos que hacer un poco de cálculo mental para asegurarnos de que los valores [0.2, 0.4, 0.6, 0.8]dividieran los datos en grupos de igual tamaño. Cada grupo tiene el 20% de los datos.

Los datos se dividen en 5 grupos donde cada grupo tiene 4 puntos de datos. Si usáramos los valores [0.2, 0.4, 0.7, 0.8], la función devolvería los cuatro valores en esos puntos de división. Sin embargo, esos valores no dividirían los datos en cinco grupos del mismo tamaño. ¡Un grupo solo tendría el 10% de los datos y otro grupo tendría el 30% de los datos!

Los datos se dividen en grupos de tamaño desigual. Un grupo tiene 6 puntos de datos y el otro grupo solo tiene 2.

Cuantiles comunes

Uno de los cuantiles más comunes es el 2-cuantil. Este valor divide los datos en dos grupos de igual tamaño. La mitad de los datos estarán por encima de este valor y la mitad de los datos estarán por debajo de él. ¡Esto también se conoce como mediana !

Los 4 cuantiles, o cuartiles , dividen los datos en cuatro grupos de igual tamaño. Encontramos los cuartiles en el ejercicio anterior. Opciones

Finalmente, los percentiles, o los valores que dividen los datos en 100 grupos, se usan comúnmente para comparar nuevos puntos de datos con el conjunto de datos. Es posible que escuche declaraciones como “Tiene una altura superior al percentil 80”. Esto significa que su altura está por encima de cualquier valor que divida el primer 80% de los datos del 20% restante.

Rango Intercuartil

Revisión de rango

Una de las estadísticas más comunes para describir un conjunto de datos es el rango . El rango de un conjunto de datos es la diferencia entre los valores máximo y mínimo. Si bien esta estadística descriptiva es un buen comienzo, es importante considerar el impacto que tienen los valores atípicos en los resultados:

En esta imagen, la mayoría de los datos están entre 0 y 15. Sin embargo, hay un gran valor atípico negativo ( -20) y un gran valor atípico positivo ( 40). Esto hace que el rango del conjunto de datos 60 (la diferencia entre 40y -20). ¡Eso no es muy representativo de la distribución de la mayoría de los datos!

El rango intercuartil (RIQ) es una estadística descriptiva que intenta solucionar este problema. El IQR ignora las colas del conjunto de datos, por lo que usted sabe el rango alrededor del cual se centran sus datos.

Cuartiles

El rango intercuartil es la diferencia entre el tercer cuartil (Q3) y el primer cuartil (Q1). Si necesita un repaso sobre los cuartiles, puede echar un vistazo a nuestra lección .

Por ahora, todo lo que necesitas saber es que el primer cuartil es el valor que separa el primer 25% de los datos del 75% restante.

El tercer cuartil es lo contrario: separa el primer 75% de los datos del 25% restante. El rango intercuartil es la diferencia entre estos dos valores.

IQR in SciPy

En el último ejercicio, calculamos el IQR encontrando los cuartiles usando NumPy y encontrando la diferencia nosotros mismos. La biblioteca SciPy tiene una función que puede calcular el IQR en un solo paso.

La función iqr() toma un conjunto de datos como parámetro y devuelve el rango intercuartil. Observe que cuando importamos iqr(), lo importamos desde el submódulo stats:

From scipy.stats import iqr

dataset = [4, 10, 38, 85, 193]
interquartile_range = iqr(dataset)

Diagramas de caja

Los diagramas de caja son una de las formas más comunes de visualizar un conjunto de datos. Al igual que los histogramas , los diagramas de caja dan una idea de la tendencia central y la dispersión de los datos.

Eche un vistazo al diagrama de caja de esta página. Este diagrama de caja visualiza un conjunto de datos que contiene la duración de 9975 canciones. Destacaremos algunas de las características del diagrama de caja y las profundizaremos con más detalle en esta lección:

• La línea en el centro del cuadro es la mediana .
• Los bordes de la caja son el primer y tercer cuartil . Esto hace que la longitud del cuadro sea el rango intercuartil : el 50% central de sus datos.
• Los bigotes del diagrama de caja se extienden para incluir la mayoría de los datos. Hay muchas formas diferentes de calcular la longitud de los bigotes.
• Los valores atípicos son puntos que quedan más allá de los bigotes. Esos puntos están representados con puntos. En el diagrama de caja que mostramos hay muchos valores atípicos.

Mediana

Al hacer un diagrama de caja, el lugar más fácil para comenzar es la línea que está dentro del cuadro. Esta línea es la mediana del conjunto de datos. La mitad de los datos están por encima de esa línea y la otra mitad por debajo de ella.

Podemos encontrar la mediana de un conjunto de datos usando la función median() de NumPy.

import numpy as np

dataset = [4, 8, 15, 16, 23]
dataset_median = np.median(dataset) 
# dataset_median stores the value 15

Rango intercuartil

Ahora que hemos dibujado la mediana, dibujemos los bordes de la caja. El cuadro se extiende al primer y tercer cuartil del conjunto de datos.

Esto divide visualmente los datos en cuartos. Una cuarta parte de los datos quedarán fuera del cuadro de la izquierda. Otra cuarta parte de los datos se ubicará entre el lado izquierdo del cuadro y la línea mediana. Un tercer cuarto de los datos se encuentra entre la línea mediana y el lado derecho del cuadro. Y el último cuarto de los datos queda fuera del cuadro de la derecha.

Al dibujar los bordes del cuadro utilizando el primer y tercer cuartil, se visualiza el rango intercuartil . La longitud del cuadro representa esta estadística descriptiva de uso común.

Podemos usar la función quantile() de NumPy para encontrar el primer y tercer cuartil:

dataset = [4, 8, 15, 16, 23]

first_quartile = np.quantile(dataset, 0.25) 
third_quartile = np.quantile(dataset, 0.75)

Bigotes

Los bigotes de un diagrama de caja muestran información relacionada con la dispersión del conjunto de datos.

Hay muchas formas diferentes de trazar los bigotes de un diagrama de caja. Es posible que vea algunos diagramas de caja donde los bigotes se extienden hasta los valores mínimo y máximo. Algunos diagramas de caja tienen bigotes que se extienden una desviación estándar desde la media de los datos.

Sin embargo, uno de los métodos más utilizados para dibujar los bigotes es extenderlos 1,5 veces el rango intercuartil desde el primer y tercer cuartil.

Por ejemplo, digamos que tiene un conjunto de datos donde el primer cuartil es 4 y el tercer cuartil es 9. El rango intercuartil de este conjunto de datos es 5.

Los bigotes se extenderían 1,5 veces la longitud del IQR. En este caso, es decir 1.5 * 5, o 7.5.

Sabemos que los bigotes extienden hasta 7.5, pero ¿por dónde empiezan? Comienzan en los bordes de la caja, o en el primer y tercer cuartil. En este caso, el bigote izquierdo comienza en el primer cuartil (4) y se extiende 7.5 unidades hacia la izquierda. Entonces el bigote izquierdo se extiende hasta -3.5. El bigote derecho comienza en el tercer cuartil (9) y se extiende hasta 16.5.

Un pequeño detalle más a tener en cuenta: los bigotes generalmente no se extienden hasta 1,5 veces el IQR. En cambio, se extienden hasta el punto más cercano 1.5 al IQR en la dirección de la mediana. Esto significa que en lugar de extenderse hasta -3.5 y 16.5, los bigotes en realidad se extenderían hasta el primer punto mayor que -3.5 y el primer punto menor que 16.5.

Valores atípicos

La última pieza de un diagrama de caja es la representación de valores atípicos. Un valor atípico es un punto del conjunto de datos que queda fuera de los bigotes. Los valores atípicos suelen representarse con un punto o un asterisco.

Diagramas de caja en Matplotlib

Pasamos esta lección construyendo un diagrama de caja a mano. ¡Veamos ahora cómo lo hace la biblioteca Matplotlib de Python!

El módulo matplotlib.pyplot tiene una función llamada boxplot(). boxplot()toma un conjunto de datos como parámetro . Este conjunto de datos podría ser algo así como una lista de números o un Pandas DataFrame.

import matplotlib.pyplot as plt

data = [1, 2, 3, 4, 5]
plt.boxplot(data)
plt.show()

Uno de los puntos fuertes de Matplotlib es la facilidad para trazar dos diagramas de caja uno al lado del otro. Si pasa boxplot() una lista de conjuntos de datos, Matplotlib creará un diagrama de caja para cada uno, lo que le permitirá comparar su distribución y tendencias centrales.

import matplotlib.pyplot as plt

dataset_one = [1, 2, 3, 4, 5]
dataset_two = [3, 4, 5, 6, 7]
plt.boxplot([dataset_one, dataset_two])
plt.show()