Regresión lineal

Introduccion

La regresión lineal es una poderosa técnica de modelado que se puede utilizar para comprender la relación entre una variable cuantitativa y una o más variables, a veces con el objetivo de hacer predicciones. Por ejemplo, la regresión lineal puede ayudarnos a responder preguntas como:

• ¿Cuál es la relación entre el tamaño de los apartamentos y el precio de alquiler de los apartamentos en Nueva York?
• ¿Es la altura de una madre un buen predictor de la altura adulta de su hijo?

El primer paso antes de ajustar un modelo de regresión lineal es el análisis exploratorio de datos y la visualización de datos: ¿existe alguna relación que podamos modelar? Por ejemplo, supongamos que recopilamos las alturas (en cm) y los pesos (en kg) de 9 adultos e inspeccionamos un gráfico de altura versus peso:

plt.scatter(data.height, data.weight)
plt.xlabel('height (cm)')
plt.ylabel('weight (kg)')
plt.show()

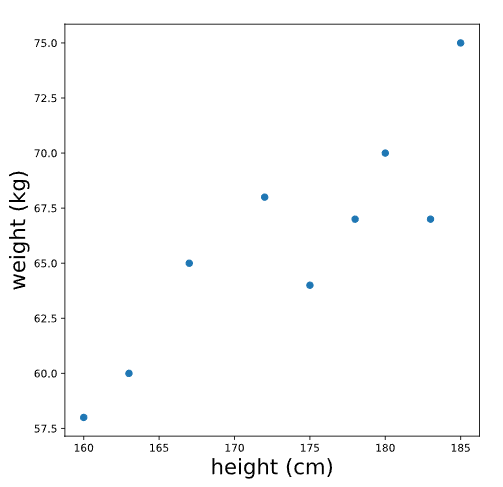
Cuando miramos este gráfico, vemos que hay cierta evidencia de una relación entre la altura y el peso: las personas más altas tienden a pesar más. En los siguientes ejercicios, aprenderemos cómo modelar esta relación con una línea. Si tuvieras que trazar una línea que pasara por estos puntos para describir la relación entre altura y peso, ¿qué línea trazarías?

Ecuación de una recta

Como su nombre lo indica, la regresión linear implica ajustar una línea a un conjunto de puntos de datos. Para ajustar una línea, es útil comprender la ecuación de una línea, que a menudo se escribe como \(y=mx+b\) . En esta ecuación:

• \(x\) e \(y\) representan variables, como altura y peso u horas de estudio y puntuaciones de exámenes .
• \(b\) representa la intersección y de la línea. Aquí es donde la línea se cruza con el eje y (una línea vertical ubicada en \(x = 0\) ). \(m\) representa la pendiente. Esto controla qué tan pronunciada es la línea. Si elegimos dos puntos cualesquiera en una recta, la pendiente es la relación entre la distancia vertical y horizontal entre esos puntos; Esto a menudo se escribe como subir/correr.

El siguiente gráfico muestra una recta con la ecuación \(y = 2x + 12\) :

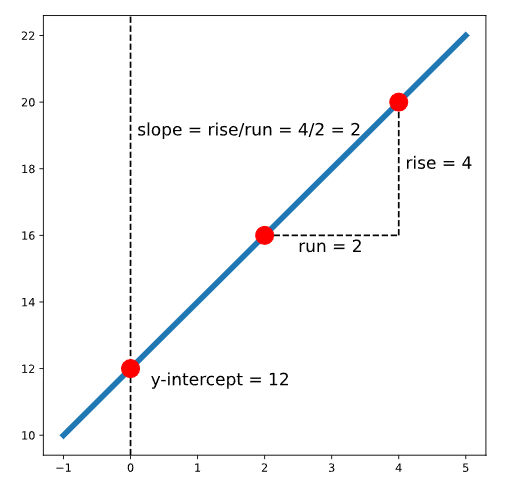
Tenga en cuenta que también podemos tener una recta con pendiente negativa. Por ejemplo, el siguiente gráfico muestra la recta con la ecuación \(y = -2x + 8\) :

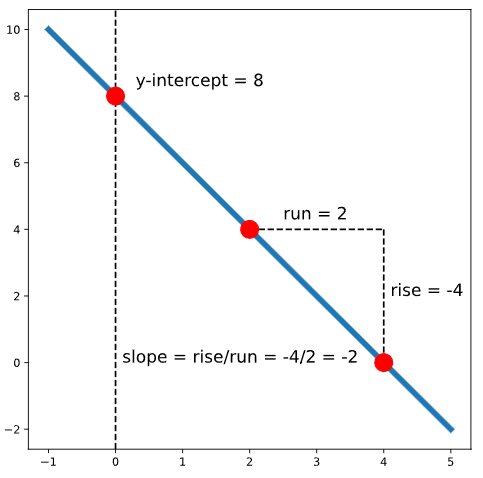
Encontrar la “mejor” línea

En el último ejercicio, intentamos imaginar cómo sería la línea que mejor se ajustaría. Para elegir realmente una línea, debemos idear algunos criterios sobre lo que realmente significa “mejor”.

Dependiendo de nuestros objetivos y datos finales, podríamos elegir diferentes criterios; sin embargo, una opción común para la regresión lineal son los mínimos cuadrados ordinarios (OLS). En una regresión MCO simple, asumimos que la relación entre dos variables \(x\) e \(y\) se puede modelar como:

\[y=mx​+b+error​​​​\]

Definimos “mejor” como la línea que minimiza el error cuadrático total para todos los puntos de datos. Este error cuadrático total se denomina función de pérdida en el aprendizaje automático. Por ejemplo, considere la siguiente trama:

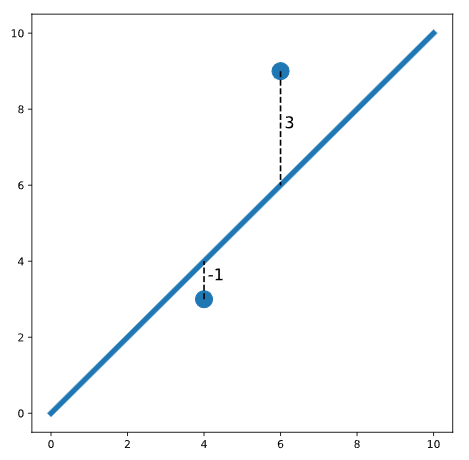
En este gráfico, vemos dos puntos a cada lado de una línea. Uno de los puntos está una unidad debajo de la línea (etiquetada -1). El otro punto está tres unidades por encima de la línea (etiquetado como 3). El error cuadrático total (pérdida) es:

\[\text{pérdida} = (-1)^2 + (3)^2 = 1 + 9 = 10\]

Observe que elevamos al cuadrado cada distancia individual de modo que los puntos por debajo y por encima de la línea contribuyan igualmente a la pérdida (cuando elevamos al cuadrado un número negativo, el resultado es positivo). Para encontrar la línea que mejor se ajusta, necesitamos encontrar la pendiente y la intersección de la línea que minimiza la pérdida.

La visualización interactiva en el navegador le permite intentar encontrar la línea que mejor se ajuste a un conjunto aleatorio de puntos de datos:

• El control deslizante de la izquierda controla la \(m\) (pendiente)
• El control deslizante de la derecha controla la \(b\) (intercepción)

Puede ver la pérdida total en el lado derecho de la visualización. Para obtener la línea de mejor ajuste, queremos que esta pérdida sea lo más pequeña posible.

Para comprobar si obtuvo la mejor línea, marque la casilla “Trazar mejor ajuste”.

Aleatoriza un nuevo conjunto de puntos e intenta ajustar una nueva línea ingresando la cantidad de puntos que deseas en el cuadro de texto y presionando Randomize Points.

Juegue con el subprograma y vea si puede encontrar la línea que mejor se ajuste a los puntos que ha aleatorizado.

• Acceso a la simulacion

Ajuste de un modelo de regresión lineal en Python

Hay varias bibliotecas de Python que se pueden usar para ajustar una regresión lineal, pero en este curso usaremos la función OLS.from_formula() de statsmodels.api porque usa una sintaxis simple y proporciona resúmenes completos del modelo.

Supongamos que tenemos un conjunto de datos nombrado body_measurements con columnas height y weight. Si queremos ajustar un modelo que pueda predecir el peso en función de la altura, podemos crear el modelo de la siguiente manera:

model = sm.OLS.from_formula('weight ~ height', data = body_measurements)

Usamos la fórmula ‘weight ~ height’ porque queremos predecir weight (es la variable de resultado) usándo height como predictor. Entonces, podemos ajustar el modelo usando .fit():

results = model.fit()

Finalmente, podemos inspeccionar un resumen de los resultados usando print(results.summary()). Por ahora, solo veremos los coeficientes usando results.params, pero la tabla de resumen completa es útil porque contiene otra información de diagnóstico importante.

print(results.params)

Salida:

Intercept   -21.67
height        0.50
dtype: float64

Esto nos dice que la intersección de mejor ajuste es -21.67 y la pendiente de mejor ajuste es 0.50.

Ejemplo:

Utilizando el conjunto de datos students, cree un modelo de regresión lineal que prediga el score del estudiante utilizando hours_studied como predictor y guarde el resultado en una variable denominada model.

import pandas as pd
import statsmodels.api as sm

# Read in the data
students = pd.read_csv('test_data.csv')

# Create the model here:
model = sm.OLS.from_formula('score ~ hours_studied', data = students)
# Fit the model here:
results = model.fit()
# Print the coefficients here:
print(results.params)

Salida

Intercept        43.016014
hours_studied     9.848111
dtype: float64

Usar un modelo de regresión para la predicción

Supongamos que tenemos un conjunto de datos de alturas y pesos de 100 adultos. Ajustamos una regresión lineal e imprimimos los coeficientes:

model = sm.OLS.from_formula('weight ~ height', data = body_measurements)
results = model.fit()
print(results.params)

Salida:

Intercept   -21.67
height        0.50
dtype: float64

Esta regresión nos permite predecir el peso de un adulto si conocemos su altura. Para hacer una predicción, necesitamos reemplazar la intersección y la pendiente en nuestra ecuación de una línea. La ecuación es:

\[peso = 0.50 * altura - 21.67\]

Para hacer una predicción, podemos introducir cualquier altura. Por ejemplo, podemos calcular que el peso esperado para una persona de 160cm de altura es de 58,33kg:

\(peso = 0.50 * 160 - 21.67\) \(peso = 58.33\)

También podemos hacer este cálculo utilizando el método .predict() del modelo ajustado. Para predecir el peso de una persona de 160 cm de altura, primero debemos crear un nuevo conjunto de datos height igual al 160 que se muestra a continuación:

newdata = {"height":[160]}
print(results.predict(newdata))

Salida:

0      58.33
dtype: float64

Tenga en cuenta que obtenemos el mismo resultado (58.33) que con los otros métodos; sin embargo, se devuelve como un marco de datos.

Ejemplo

Continuando con el ejemplo anterior teniamos los coeficientes:

print(results.params)

Salida

Intercept        43.016014
hours_studied     9.848111
dtype: float64

Utilizando este modelo, ¿cuál es la puntuación prevista para un estudiante que pasó 3 horas estudiando? Podemos calcular la probabilidad utilizando la formula de la linea y el metodo predict().

pred_3hr = results.params[1]*3 + results.params[0]
print(pred_3hr)

# Calculate and print `pred_5hr` here:
newdata = {"hours_studied":[5]}
pred_5hr = results.predict(newdata)
print(pred_5hr)

Interpretar el Modelo de Regression

Inspeccionemos nuevamente el resultado de una regresión que predice el peso en función de la altura. La línea de regresión se parece a esto:

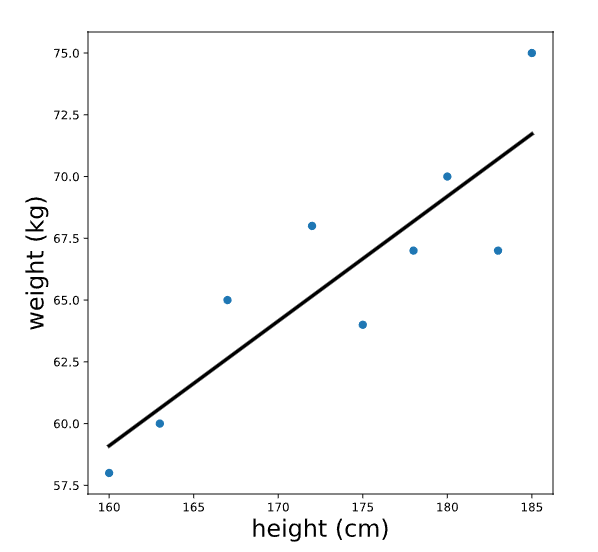
Tenga en cuenta que las unidades de la intersección y la pendiente de una recta de regresión coinciden con las unidades de las variables originales; la intersección de esta línea se mide en kg y la pendiente se mide en kg/cm. Para que la intersección (que calculamos anteriormente como -21.67kg) tenga sentido, alejemos este gráfico:

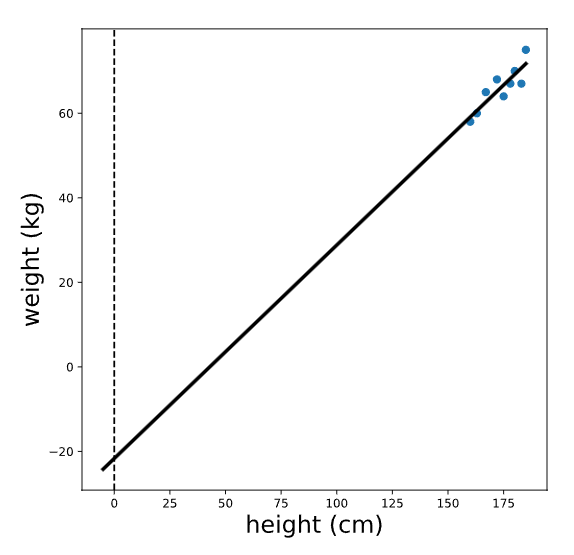
Vemos que la intersección es el valor predicho de la variable de resultado (peso) cuando la variable predictora (altura) es igual a cero. En este caso, la interpretación del origen es que se espera que una persona de 0 cm de altura pese -21 kg. ¡Esto no tiene sentido porque es imposible que alguien mida 0 cm de altura!

Sin embargo, en otros casos, este valor tiene sentido y es útil interpretarlo. Por ejemplo, si predijeramos las ventas de helado en función de la temperatura, la intersección serían las ventas esperadas cuando la temperatura sea 0 grados.

Para visualizar la pendiente, acerquemos nuestro gráfico:

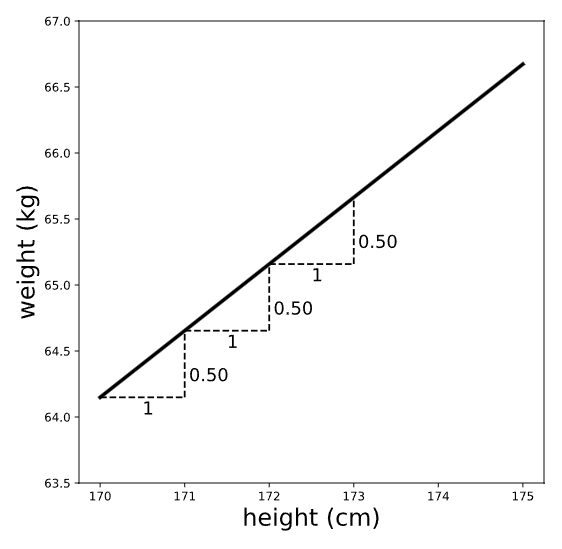
Recuerde que la pendiente se puede considerar como subida/corrida: la relación entre las distancias vertical y horizontal entre dos puntos cualesquiera de la línea. Por lo tanto, la pendiente (que previamente calculamos en 0.50kg/cm) es la diferencia esperada en la variable de resultado (peso) para una diferencia de una unidad en la variable predictiva (altura). En otras palabras, esperamos que una diferencia de altura de un centímetro se asocie con 0,5 kilogramos adicionales de peso.

Tenga en cuenta que la pendiente nos da dos datos: la magnitud Y la dirección de la relación entre las variables \(x\) e \(y\). Por ejemplo, supongamos que en lugar de eso ajustamos una regresión de peso con minutos de ejercicio por día como predictor y calculamos una pendiente de -.1. Interpretaríamos que esto significa que se espera que las personas que hacen ejercicio durante un minuto adicional al día pesen 0,1 kg MENOS.

Supuestos de regresión lineal Parte 1

Hay una serie de supuestos de regresión lineal simple, que es importante comprobar si se está ajustando a un modelo lineal. El primer supuesto es que la relación entre la variable de resultado y el predictor es lineal (puede describirse mediante una línea). Podemos verificar esto antes de ajustar la regresión simplemente mirando una gráfica de las dos variables.

Los dos supuestos siguientes (normalidad y homocedasticidad) son más fáciles de comprobar después de ajustar la regresión. Aprenderemos más sobre estos supuestos en los siguientes ejercicios, pero primero necesitamos calcular dos cosas: valores ajustados y residuos .

Considere nuevamente nuestro modelo de regresión para predecir el peso en función de la altura (fórmula del modelo ‘weight ~ height’). Los valores ajustados son los pesos previstos para cada persona en el conjunto de datos que se utilizó para ajustar el modelo, mientras que los residuos son las diferencias entre el peso previsto y el peso real de cada persona. Visualmente:

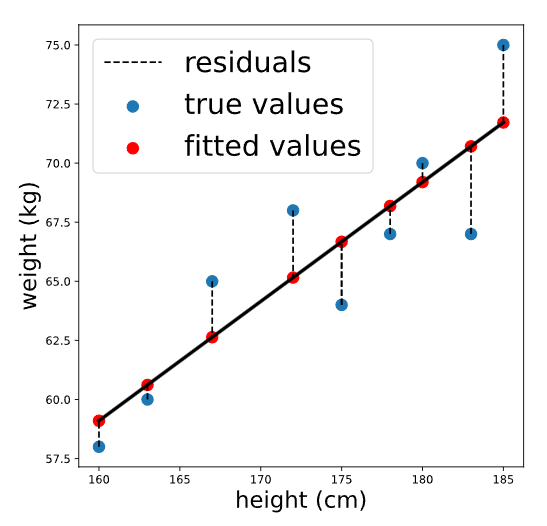
Podemos calcular los valores ajustados .predict()pasando los datos originales. El resultado es una serie de pandas que contiene valores predichos para cada persona en el conjunto de datos original:

fitted_values = results.predict(body_measurements)
print(fitted_values.head())

Salida:

0    66.673077
1    59.100962
2    71.721154
3    70.711538
4    65.158654
dtype: float64

Los residuales son las diferencias entre cada uno de estos valores ajustados y los valores verdaderos de la variable de resultado. Se pueden calcular restando los valores ajustados de los valores reales. Podemos realizar esta resta de elementos en Python simplemente restando una serie de Python de la otra, como se muestra a continuación:

residuals = body_measurements.weight - fitted_values
print(residuals.head())

Salida

0   -2.673077
1   -1.100962
2    3.278846
3   -3.711538
4    2.841346
dtype: float64

Una vez que hayamos calculado los valores ajustados y los residuos de un modelo, podemos verificar los supuestos de normalidad y homocedasticidad de la regresión lineal.

Supuesto de normalidad

El supuesto de normalidad establece que los residuos deben distribuirse normalmente. Se hace esta suposición porque, estadísticamente, los residuos de cualquier conjunto de datos independiente se aproximarán a una distribución normal cuando el conjunto de datos sea lo suficientemente grande. Para obtener más información sobre esto, haga clic aquí .

Para comprobar el supuesto de normalidad, podemos inspeccionar un histograma de los residuos y asegurarnos de que la distribución parezca aproximadamente normal (sin sesgos ni múltiples “jorobas”):

plt.hist(residuals)
plt.show()

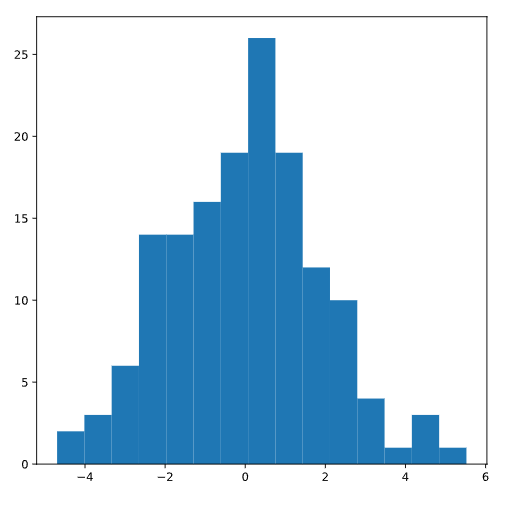
Estos residuos aparecen distribuidos normalmente, lo que nos lleva a concluir que se cumple el supuesto de normalidad.

Si, en cambio, el gráfico se pareciera a la siguiente distribución (que está sesgada hacia la derecha), nos preocuparía que no se cumpliera el supuesto de normalidad:

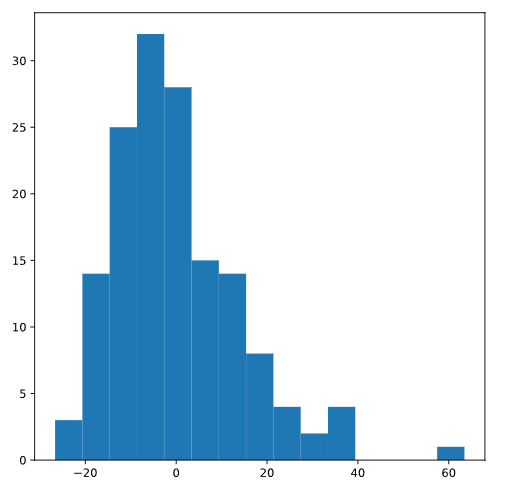
Supuesto de homocedasticidad

La homocedasticidad es una forma elegante de decir que los residuos tienen la misma variación en todos los valores de la variable predictiva (independiente). Cuando no se cumple la homocedasticidad, esto se llama heterocedasticidad, lo que significa que la variación en el tamaño del término de error difiere entre la variable independiente.

Dado que una regresión lineal busca minimizar los residuos y otorga el mismo peso a todas las observaciones, la heteroscedasticidad puede generar sesgos en los resultados.

Una forma común de comprobar esto es trazando los residuos frente a los valores ajustados.

plt.scatter(fitted_values, residuals)
plt.show()

Predictores categóricos

En los ejercicios anteriores, usamos un predictor cuantitativo en nuestra regresión lineal, pero es importante señalar que también podemos usar predictores categóricos. El caso más simple de un predictor categórico es una variable binaria (solo dos categorías).

Por ejemplo, supongamos que encuestamos a 100 adultos y les pedimos que informaran su altura en cm y si juegan o no baloncesto. Hemos codificado la variable bball_player para que sea igual a 1 si la persona juega baloncesto y 0 si no. A continuación se muestra un gráfico de height vs bball_player:

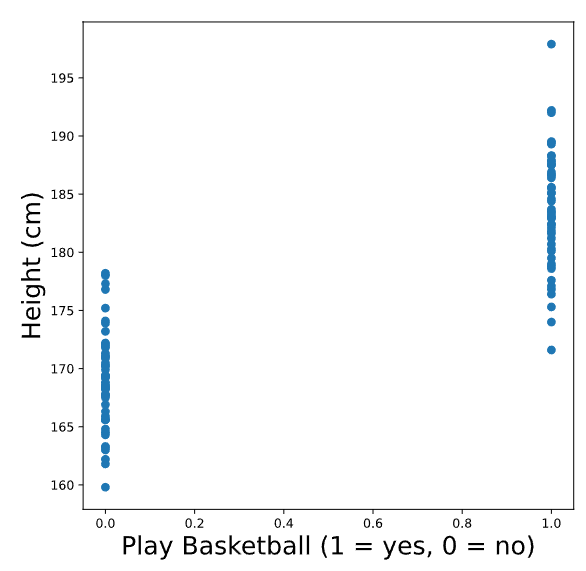
Vemos que las personas que juegan baloncesto tienden a ser más altas que las que no lo hacen. Al igual que antes, podemos dibujar una línea que se ajuste a estos puntos. ¡Tómate un momento para pensar en cómo se vería esa línea!

Es posible que hayas adivinado (¡correctamente!) que la línea que mejor se ajusta a esta gráfica es la que pasa por la altura media de cada grupo. Para recrear el diagrama de dispersión con la línea de mejor ajuste, podríamos usar el siguiente código:

# Calculate group means
print(data.groupby('play_bball').mean().height)

Salida:

	jugar_bball
0	169.016
1	183.644

Esto generará el siguiente gráfico (sin etiquetas ni colores adicionales):

# Create scatter plot
plt.scatter(data.play_bball, data.height)

# Add the line using calculated group means
plt.plot([0,1], [169.016, 183.644])

# Show the plot
plt.show()

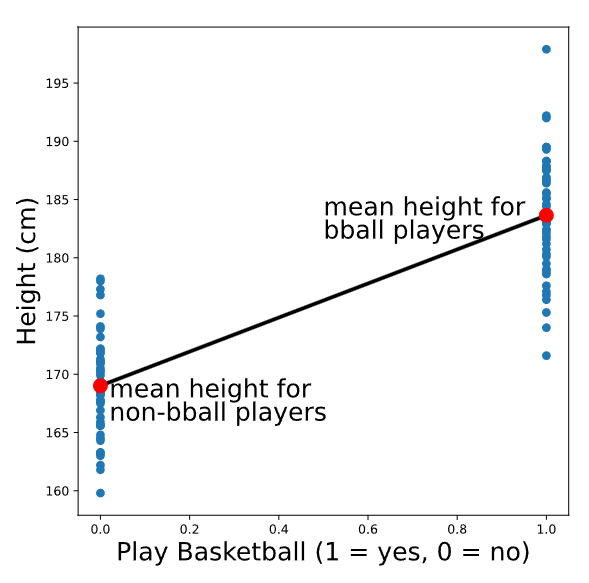
Predictores categóricos: ajuste e interpretación

Ahora que hemos visto cómo se ve visualmente un modelo de regresión con un predictor binario, podemos ajustar el modelo usando statsmodels.api.OLS.from_formula(), de la misma manera que lo hicimos con un predictor cuantitativo:

model = sm.OLS.from_formula('height ~ play_bball', data)
results = model.fit()
print(results.params)

Salida

Intercept     169.016
play_bball     14.628
dtype: float64

Tenga en cuenta que esto funcionará si la variable play_bball está codificada con 0 y 1, pero también funcionará si está codificada con True y False, o incluso si está codificada con cadenas como ‘yes’y ‘no’(en este caso, la etiqueta del coeficiente se verá algo como play_bball[T.yes] en la salida params, indicando que ‘yes’corresponde a 1).

Para interpretar este resultado, primero debemos recordar que la intersección es el valor esperado de la variable de resultado cuando el predictor es igual a cero. En este caso, la intersección es, por tanto, la altura media de los jugadores que no son jugadores de baloncesto.

La pendiente es la diferencia esperada en la variable de resultado para una diferencia de una unidad en la variable predictiva. En este caso, una diferencia de una unidad play_bballes la diferencia entre no ser jugador de baloncesto y ser jugador de baloncesto. Por lo tanto, la pendiente es la diferencia en las alturas medias de los jugadores de baloncesto y los que no lo son.

Regresión lineal con un predictor categórico

Aprenda a ajustar e interpretar un modelo lineal con un predictor categórico que tiene más de dos categorías.

Introducción

La regresión lineal es una técnica de aprendizaje automático que se puede utilizar para modelar la relación entre una variable cuantitativa y algunas otras variables. Esas otras variables pueden ser cuantitativas (por ejemplo, altura o salario) o categóricas (por ejemplo, industria laboral o color de cabello). Sin embargo, si queremos incluir predictores categóricos en un modelo de regresión lineal, debemos tratarlos de manera un poco diferente a las variables cuantitativas. Este artículo explorará la implementación e interpretación de un único predictor categórico con más de dos categorías.

Los datos

Como ejemplo, usaremos un conjunto de datos de StreetEasy que contiene información sobre alquileres de viviendas en la ciudad de Nueva York. Por ahora, sólo nos centraremos en dos columnas de este conjunto de datos:

• rent: el precio de alquiler de cada apartamento
• borough: el municipio donde se encuentra el apartamento, con tres valores posibles ( ‘Manhattan’, ‘Brooklyn’, y ‘Queens’)

Las primeras cinco filas de datos se imprimen a continuación:

import pandas as pd
rentals = pd.read_csv('rentals.csv')
print(rentals.head(5))

	alquilar	ciudad
0	5295	Brooklyn
1	4020	manhattan
2	16000	manhattan
3	3150	reinas
4	2955	reinas

La matriz X

Para comprender cómo podemos ajustar un modelo de regresión con un predictor categórico, es útil analizar lo que sucede cuando utilizamos statsmodels.api.OLS.from_formula() para crear un modelo. Cuando pasamos una fórmula a esta función (como 'weight ~ height'o 'rent ~ borough'), en realidad crea un nuevo conjunto de datos, que no vemos. Este nuevo conjunto de datos a menudo se denomina matriz X y se utiliza para ajustar el modelo.

Cuando usamos un predictor cuantitativo, la matriz X se ve similar a los datos originales, pero con una columna adicional de 1s al frente (el razonamiento detrás de esta columna de 1s es el tema de un artículo futuro; por ahora, no hay necesidad de preocuparse por ¡él!). Sin embargo, cuando ajustamos el modelo con un predictor categórico, sucede algo más: terminamos con columnas adicionales de 1s y 0s.

Por ejemplo, digamos que queremos ajustar una predicción de regresión rent basada en borough. Podemos ver la matriz X para este modelo usando patsy.dmatrices(), que se implementa detrás de escena en statsmodels:

import pandas as pd
import patsy

rentals = pd.read_csv('rentals.csv')
y, X = patsy.dmatrices('rent ~ borough', rentals)

# Print out the first 5 rows of X
print(X[0:5])

Salida

[[1. 0. 0.]
 [1. 1. 0.]
 [1. 1. 0.]
 [1. 0. 1.]
 [1. 0. 1.]]

La primera columna es toda 1s, tal como la obtendríamos para un predictor cuantitativo; pero las dos segundas columnas se formaron en función de la variable borough. Recuerde que los primeros cinco valores de la columna borough se veían así:

ciudad Brooklyn manhattan manhattan reinas reinas

Tenga en cuenta que la segunda columna de la matriz X [0, 1, 1, 0, 0] es una variable indicadora de Manhattan: es igual a 1 cuando borough is 'Manhattan' y 0 en caso contrario. Mientras tanto, la tercera columna de la matriz X ([0, 0, 0, 1, 1])es un indicador de la variable ‘Queens’ que es igual a 1 cuando borough is 'Queens' y 0 en caso contrario.

La matriz X no contiene una variable indicadora para Brooklyn. Esto se debe a que este conjunto de datos solo contiene tres valores posibles de borough: ‘Brooklyn’, ‘Manhattan’y ‘Queens’. Para recrear la columna borough, solo necesitamos dos columnas indicadoras, porque cualquier apartamento que no esté ‘Manhattan’o ‘Queens’deba estarlo ‘Brooklyn’. Por ejemplo, la primera fila de la matriz X tiene 0s en ambas columnas del indicador, lo que indica que el apartamento debe estar en Brooklyn. Matemáticamente decimos que un indicador ‘Brooklyn’ crea colinealidad en la matriz X. En inglés normal: un indicador ‘Brooklyn’ no añade ninguna información nueva.

Debido a ‘Brooklyn’ falta en la matriz X, es la categoría de referencia para este modelo.

Implementación e interpretación

Ahora ajustemos un modelo de regresión lineal usando statsmodel e imprimamos los coeficientes del modelo:

import statsmodels.api as sm
model = sm.OLS.from_formula('rent ~ borough', rentals).fit()
print(model.params)

Salida

Intercept               3327.403751
borough[T.Manhattan]    1811.536627
borough[T.Queens]       -811.256430
dtype: float64

En el resultado, vemos dos pendientes diferentes: una para borough[T.Manhattan] y otra para borough[T.Queens], que son las dos variables indicadoras que vimos en la matriz X. Podemos usar la intersección y dos pendientes para construir la siguiente ecuación para predecir el alquiler:

\[rent = 3327.4 + 1811.5 ∗ borough[T.Manhattan] − 811.3 ∗ borough[T.Queens]\]

Para comprender e interpretar esta ecuación, podemos construir ecuaciones separadas para cada distrito:

Ecuación 1: Brooklyn

Cuando un apartamento está ubicado en Brooklyn, ambos borough[T.Manhattan] y borough[T.Queens] serán iguales a cero y la ecuación queda:

\(rent = 3327.4 + 1811.5 ∗ 0−811.3 ∗ 0\) \(rent = 3327.4\) ​ En otras palabras, el intercepto es el precio de alquiler previsto (promedio) de un apartamento en Brooklyn (la categoría de referencia).

Ecuación 2: Manhattan

Cuando un apartamento está ubicado en Manhattan, borough[T.Manhattan] = 1 y borough[T.Queens] = 0. La ecuación se convierte en:

\(rent = 3327.4 + 1811.5 ∗ 1 − 811.3 ∗ 0\) \(rent = 3327.4 + 1811.5\) \(rent = 5138.9\)

Vemos que el precio de alquiler (promedio) previsto para un apartamento en Manhattan es 3327,4 + 1811,5 : el intercepto (que es el precio promedio en Brooklyn) más la pendiente de borough[T.Manhattan]. Por tanto, podemos interpretar la pendiente borough[T.Manhattan] como la diferencia en el precio medio de alquiler entre apartamentos en Brooklyn (la categoría de referencia) y Manhattan.

Ecuación 3: Reinas

Cuando un apartamento está ubicado en Queens, borough[T.Manhattan] = 0 y borough[T.Queens] = 1. La ecuación se convierte en:

\(rent = 3327.4 + 1811.5 ∗ 0 − 811.3 ∗ 1\) \(rent = 3327.4 − 811.3\) \(rent = 2516.1\) ​ Vemos que el precio de alquiler previsto (promedio) para un apartamento en Queens es 3327,4 - 811,3 : el intercepto (que es el precio promedio en Brooklyn) más la pendiente borough[T.Queens] (que resulta ser negativa porque los apartamentos en Queens son menos costosos que los apartamentos en Brooklyn). Por tanto, podemos interpretar la pendiente borough[T.Queens] como la diferencia en el precio medio de alquiler entre apartamentos en Brooklyn (la categoría de referencia) y Queens.

Podemos verificar nuestra comprensión de todos estos coeficientes imprimiendo los precios medios de alquiler por municipio:

print(rentals.groupby('borough').mean())

Salida

                 rent
borough               
Brooklyn   3327.403751
Manhattan  5138.940379
Queens     2516.147321

¡Los precios promedio en cada distrito arrojan exactamente los mismos valores que predijimos según el modelo de regresión lineal! Por ahora, esto puede parecer una forma demasiado complicada de recuperar los precios medios de alquiler por municipio, pero es importante entender cómo funciona para construir modelos de regresión lineal más complejos en el futuro.

Cambiar la categoría de referencia

En el ejemplo anterior, vimos que esa 'Brooklyn' era la categoría de referencia predeterminada (porque aparece primero alfabéticamente), pero podemos cambiar fácilmente la categoría de referencia en el modelo de la siguiente manera:

model = sm.OLS.from_formula('rent ~ C(borough, Treatment("Manhattan"))', rentals).fit()
print(model.params)

Salida:

Intercept                                         5138.940379
C(borough, Treatment("Manhattan"))[T.Brooklyn]   -1811.536627
C(borough, Treatment("Manhattan"))[T.Queens]     -2622.793057
dtype: float64

En este ejemplo, la categoría de referencia es ‘Manhattan’. Por lo tanto, la intersección es el precio medio de alquiler en Manhattan y las otras pendientes son las diferencias medias de Brooklyn y Queens en comparación con Manhattan.

Otras bibliotecas de Python para ajustar modelos lineales

Existen algunas bibliotecas de Python diferentes que se pueden utilizar para ajustar modelos de regresión lineal. Por lo tanto, es importante comprender en qué se diferencia esta implementación para cada biblioteca. En statsmodels, la creación de la matriz X ocurre completamente “entre bastidores” una vez que pasamos una fórmula modelo.

En scikit-learn (otra biblioteca popular para regresión lineal), en realidad necesitamos construir las variables indicadoras nosotros mismos. Tenga en cuenta que no tenemos que construir la columna adicional de 1s que vimos en la matriz X; esto también sucede detrás de escena en scikit-learn. Para construir esas variables indicadoras, la función de pandas get_dummies() es extremadamente útil:

import pandas as pd 
rentals = pd.get_dummies(rentals, columns = ['borough'], drop_first = True)
print(rentals.head())

Producción: | |rent |borough_Manhattan| borough_Queens| |0 |5295 | 0 | 0 |1 |4020 |1 | 0 |2 |16000 |1 | 0 |3 |3150 | 0 | 1 |4 |2955 | 0 | 1

La configuración drop_first = True le dice a Python que elimine la primera variable indicadora ('Brooklyn' en este caso), que es lo que necesitamos para la regresión lineal. Luego podemos ajustar exactamente el mismo modelo usando scikit-learn la siguiente manera:

from sklearn.linear_model import LinearRegression

X = rentals[['borough_Manhattan', 'borough_Queens']]
y = rentals[['rent']]

# Fit model
regr = LinearRegression()
regr.fit(X, y)
print(regr.intercept_)
print(regr.coef_)

Salida

LinearRegression()
[3327.40375123]
[[1811.5366274  -811.25642981]]