Temas

• Asignacion de Probabilidades
• Axiomas de la Probabilidad
• Regla de la Suma
• Regla de multiplicación
• Diagrama de Arbol
• Derivaciones de axiomas de probabilidad
• Analisis utilizando una Tabla de contingencia
• La probabilidad condicional
• Probabilidad condicional en la Ley de Probabilidad Total
• Independencia de los modelos de probabilidad
• Modelos de probabilidad de Independencia condicional
• Regla de Bayes
• Proyecto: crear un Clasificador de Bayes desde cero

Asignación de Probabilidades: Ley de Laplace

Modelo de Probabilidad

El modelo de probabilidad es un marco conceptual y matemático esencial en estadística y teoría de probabilidad que permite analizar y predecir el comportamiento de fenómenos aleatorios. Este modelo se basa en dos pilares fundamentales: la definición del espacio muestral que se aborda en la seccion anterior y la asignación de probabilidades a los eventos dentro de este espacio.

El objetivo principal de un modelo de probabilidad es establecer una regla (la ley de probabilidad) que asigne valores no negativos a los subconjuntos del espacio muestral, reflejando nuestra confianza o creencia en la ocurrencia de esos eventos. Estos valores se conocen como probabilidades y representan nuestra estimación de qué tan probable es que un resultado específico, o un conjunto de resultados, ocurra. desarrolla esto

Asignacion de Probabilidades

La asignación de probabilidades es el proceso mediante el cual se atribuyen valores numéricos a los eventos en el espacio muestral, reflejando la confianza o la creencia en la ocurrencia de esos eventos. La probabilidad de un evento \(A\), denotada como \(P(A)\), es un número no negativo, entre 0 y 1, que indica qué tan probable es que \(A\) ocurra cuando se realiza el experimento.

Ley de Laplace

También conocida como la regla de la probabilidad clásica o equiprobable, establece que si un experimento aleatorio tiene resultados igualmente probables, entonces la probabilidad de un evento \(𝐸\) es el número de resultados en \(\|E\|\) dividido por el número total de resultados posibles en el espacio muestral \(\|S\|\).

\[P(E) = \frac{|E|}{|S|}\]

Ejemplo Práctico

Imagina que un bol contiene 3 bolas rojas y 2 bolas azules. Si se va a extraer una bola al azar, la probabilidad de sacar una bola roja, usando la Ley de Laplace, se calcula como el número de bolas rojas dividido por el número total de bolas:

\[P(\text{Roja}) = \frac{3}{5}\]

Si no supiéramos los colores de las bolas en el bol, pero sabemos que hay 5 bolas, y asumimos equiprobabilidad (ignorando cualquier información adicional), la probabilidad de sacar cualquier bola específica sería:

\[P(\text{Roja}) = \frac{1}{5}\]

Axiomas de la Probabilidad

Son las reglas fundamentales para definir las probabilidades de los eventos dentro del marco de la teoría de probabilidad. Estos axiomas son esenciales para construir modelos de probabilidad que permitan analizar y predecir el comportamiento de fenómenos aleatorios de manera matemáticamente rigurosa. Hay tres axiomas principales de probabilidad, y a partir de ellos se pueden derivar diversas reglas y propiedades.

Axioma 1: No Negatividad

El primer axioma establece que la probabilidad de cualquier evento es siempre un número no negativo. Esto refleja la idea de que la probabilidad mide la confianza o expectativa de que un evento ocurra, lo cual no puede ser una cantidad negativa. Este axioma también permite que la probabilidad de un evento sea cero, lo que indica que el evento es imposible dentro del contexto del experimento.

Axioma 2: Aditividad, Regla de la Suma

La regla de la suma, también conocida como la regla de adición, es un principio fundamental en la teoría de probabilidades que se utiliza para calcular la probabilidad de que ocurra al menos uno de dos eventos.

1 - Eventos Mutuamente Excluyentes

Para dos eventos \(A\) y \(B\) que no pueden ocurrir al mismo tiempo (es decir, son mutuamente excluyentes), la regla de la suma establece que la probabilidad de que ocurra \(A\) o \(B\) es simplemente la suma de sus probabilidades individuales:

\[P(A \cup B) = P(A) + P(B)\]

Por ejemplo, si tienes un mazo de cartas y quieres saber la probabilidad de sacar un rey o una reina, sumarías la probabilidad de sacar un rey con la probabilidad de sacar una reina, dado que no puedes sacar una carta que sea ambos a la vez.

2 - Eventos No Mutuamente Excluyentes

Cuando los eventos pueden ocurrir simultáneamente (es decir, no son mutuamente excluyentes), se debe ajustar la regla de la suma para evitar contar dos veces la intersección de los eventos. La regla modificada es:

\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]

Esto significa que se suma la probabilidad de \(A\) y \(B\), pero se resta la probabilidad de que \(A\) y \(B\) ocurran al mismo tiempo. Este ajuste es necesario para obtener una medida precisa de la probabilidad de que ocurra cualquiera de los eventos.

Ejemplos Prácticos de eventos no excluyentes

1. Cartas:
   • Si tienes un mazo de 52 cartas y quieres saber la probabilidad de sacar un as o un corazón, primero sumarías la probabilidad de sacar un as \(4/52\) con la probabilidad de sacar un corazón \(13/52\). Luego, restarías la probabilidad de sacar un as de corazones, la intersección de los eventos \(1/52\):
     • Sacar un As, 4 cartas: \(P(A) = \frac{4}{52}\)
     • Sacar un corazon (5, 6): \(P(B) = \frac{13}{52}\)
     • Sacar el As de corazones, 1 carta: \(P(A \cap B) = \frac{1}{52}\)
     \[P(\text{As} \cup \text{Corazón}) = \frac{4}{52} + \frac{13}{52} - \frac{1}{52} = \frac{16}{52} = \frac{4}{13}\]

     Los datos puedes darse de tres maneras: \(\frac{4}{13}\), 0,3076 o como porcentaje multiplicando el resultado anterior por 100: 30,76%.

2. Dados:
   • Si lanzas un dado y quieres saber la probabilidad de obtener un número impar o un número mayor que 4, primero determinarías la probabilidad de cada uno de estos eventos y luego su intersección:
     • Número impar (1, 3, 5): \(P(A) = \frac{3}{6}\)
     • Número mayor que 4 (5, 6): \(P(B) = \frac{2}{6}\)
     • Número impar y mayor que 4 (5): \(P(A \cap B) = \frac{1}{6}\)

     Aplicando la regla de la suma:

   \[P(A \cup B) = \frac{3}{6} + \frac{2}{6} - \frac{1}{6} = \frac{4}{6} = \frac{2}{3}\]
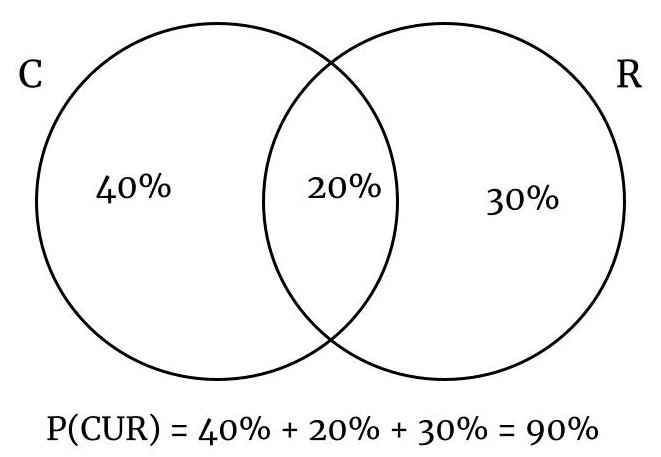
3. Sala de espera
   • En la sala de espera de un consultorio medico, el 60% de los pacientes toma cafe, el 50% lee revistas y unicamente el 20% delas personas toma cafe mientras lee revistas. Si se selecciona un paciente al azar ¿cual es la probabilidad de que tome cafe o lea revistas?
   • C = pacientes que toman cafe
   • R = Pacientes que leen revistas
   • \[P(C \cup R) = 60\% + 50\% - 20\% = 90\%\]

   

4. Solucion utilizando una Tabla
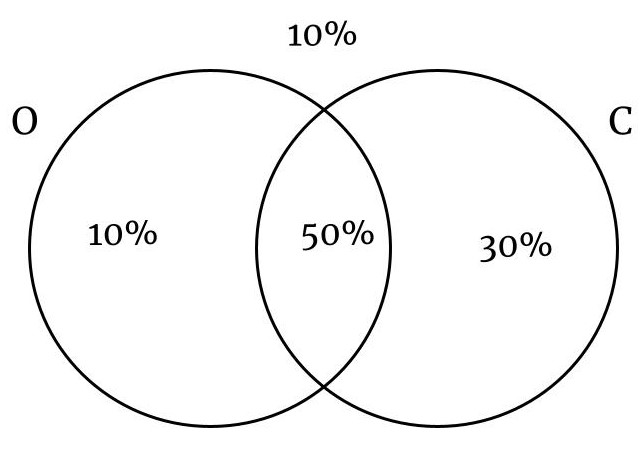
   • En una ciudad el 60% de las personas tienen ojos negros, el 80% tienen cabello negro y el 50% tienen cabello negro y ojos negros. Si se selecciona una persona al azar, calcule la probabilidad que:
     1. No tenga los ojos negros.
     2. Tenga los ojos o cabello negro
   • O = Personas con ojos negros
   • C = Personas con cabellos negros

Solucion a traves de una tabla de contingencia:

	O Negros	O No Negros	Total
C Negros	50%	30%	80%
C No Negros	10%	10%	20%
Total	60%	40%	100%

Probabilidad de que no tenga ojos negros: 40%
Personas con ojos o cabellos negros:

\[P(O\cup C) = P(O) + P(C) - P(O\cup C) = 60\% + 80\% - 50\% = 90\%\]

Axioma 3: Regla de multiplicación

La Regla de Multiplicación en probabilidad es una herramienta fundamental para calcular la probabilidad de que ocurran dos o más eventos independientes o dependientes sucesivamente. Esta regla se aplica en dos formas principales, dependiendo de si los eventos son independientes o dependientes.

1. Eventos Independientes

Cuando los eventos son independientes, la probabilidad de que todos ocurran es simplemente el producto de sus probabilidades individuales. Esto se debe a que la ocurrencia de un evento no afecta la probabilidad de ocurrencia de otro.

Fórmula:

\[P(A \cap B) = P(A) \times P(B)\]

Donde \(P(A \cap B)\) es la probabilidad de que ocurran tanto \(A\) como \(B\), y \(P(A)\) y \(P(B)\) son las probabilidades de que ocurran \(A\) y \(B\), respectivamente.

Ejemplo: Si la probabilidad de sacar una carta roja de una baraja estándar es \(\frac{1}{2}\) y la probabilidad de sacar un rey es \(\frac{1}{13}\), entonces la probabilidad de sacar una carta que sea tanto roja como un rey (asumiendo que cada extracción es independiente, como volver a meter la carta en la baraja y barajar de nuevo) es:

\[P(\text{Rey Rojo}) = \frac{1}{2} \times \frac{1}{13} = \frac{1}{26}\]

2. Eventos Dependientes

Cuando los eventos son dependientes, la probabilidad de la conjunción de eventos depende de la ocurrencia de los eventos anteriores.

Fórmula:

\[P(A \cap B) = P(A) \times P(B \mid A)\]

Donde \(P(B \mid A)\) es la probabilidad de que ocurra \(B\) dado que \(A\) ya ha ocurrido.

Ejemplo:

Si sacas una carta de una baraja de 52 cartas y quieres saber la probabilidad de que la primera carta sea un as y la segunda también sea un as, utilizarías la regla de multiplicación para eventos dependientes:

\[\begin{aligned} P(\text{As en primera carta}) = \frac{4}{52} \\ P(\text{As en segunda carta} \mid \text{As en primera carta}) = \frac{3}{51} \\ P(\text{Dos Ases}) = \frac{4}{52} \times \frac{3}{51} \end{aligned}\]

Ejercicios Eventos dependientes

Ejercicio 1
En una urna hay 5 canicas azules, 2 rojas y una verde. Si se sacan canicas consecutivas al azar sin remplazo, calcule la probabilidad que:

• La primera sea azul y la segunda sea verde.
• Las dos sean rojas

Calcular la probabilidad de que la primera canica sea azul \(A\) y la segunda sea verde \(V\)

\[P(A∩V) = P(A) * P(V|A) = \frac{5}{8} * \frac{1}{7} = \frac{5}{56} = 0.089 = 8,9%\]

la probabilidad de que las dos sean rojas \(R\):

\[P(R∩R) = P(R) * P(R|R) = \frac{2}{8} * \frac{1}{7} = \frac{2}{56} = 0.035 = 3,5%\]

Ejercicio 2: En una clase hay 10 niños y 8 niñas, si se seleccionan 3 estudiantes al azar:

• ¿Cual es la probabilidad de que todos sean niños?
• ¿Cual es la probabilidad de que todos sean niñas?

Probabilidad de que todos sean niños:

\[\begin{aligned} P(Nº∩Nº∩Nº) = P(Nº) * P(Nº|Nº) * P(Nº|Nº∩Nº) \\ P(Nº∩Nº∩Nº) = \frac{10}{18} * \frac{9}{17} * \frac{8}{16} \\ P(Nº∩Nº∩Nº) = \frac{5}{34} = 0.147 = 14,7\% \\ \end{aligned}\]

Probabilidad de que todos sean niñas:

\[\begin{aligned} P(Nª∩Nª∩Nª) = P(Nª) * P(Nª|Nª) * P(Nª|Nª∩Nª) \\ P(Nª∩Nª∩Nª) = \frac{8}{18} * \frac{7}{17} * \frac{6}{16} \\ P(Nª∩Nª∩Nª) = \frac{336}{4896} = 0.068 = 6,8\% \\ \end{aligned}\]

Una forma de visualizar todos los resultados posibles de un par de eventos es un diagrama de árbol .

Ejercicio 3:En un curso el 80% de los estudiantes aprueba matematicas, el 75% aprueba ingles. De los estudiantes que apueban matematicas, el 90% tambien aprueban ingles. Si se selecciona un estudiante al azar y este ha aprovado ingles, que probabilidades hay de que haya aprovado matematicas?

• Probabilidad de que aprueben matematicas: \(P(M) = 80\%\)
• Probabilidad de que aprueben Ingles: \(P(I) = 75\%\)
• Probabilidad de que aprueben Ingles dado que hayan aprobado matematicas: \(P(I\|M) = 90\%\)

Para calcular la probabilidada de la interseccion, o sea de que haya aprobado las dos asignaturas, que se necesita para calcular el resultado

\[\begin{aligned} P(M \cap I) = P(M) * P(I|M) \\ P(M \cap I) = 0.8 * 0.9 \\ P(M \cap I) = 0.72 = 72\% \\ \end{aligned} \\\]

Calcular el resultado del ejercicio.

\[\begin{aligned} P(M|I) = \frac{P(M \cap I)}{P(I)} \\ P(M|I) = \frac{72\%}{75\%} \\ P(M|I) = 0.96 = 96\% \\ \end{aligned}\]

El diagrama de arbol

Un diagrama de árbol es una herramienta gráfica utilizada en estadística para representar todas las posibles consecuencias de una serie de decisiones o eventos sucesivos. Este tipo de diagrama es útil para visualizar el espacio muestral de un proceso aleatorio, especialmente cuando este proceso implica varios pasos o decisiones secuenciales.

Características de un Diagrama de Árbol

1. Nodos: Puntos que representan los eventos o las decisiones. Los nodos iniciales se llaman nodos raíz, y los nodos al final de cada rama se llaman nodos hoja.
2. Ramas: Conexiones entre nodos que representan el paso de un evento o decisión a otro. Cada rama está etiquetada con la probabilidad de pasar del nodo anterior al siguiente.

Cómo Crear un Diagrama de Árbol

Paso 1: Definir el Problema

Determina los eventos o decisiones que necesitas analizar. Establece claramente cuáles son las opciones o posibles resultados en cada etapa.

Paso 2: Dibujar el Diagrama

• Nodo Inicial: Comienza con un nodo que represente el punto de partida del proceso o la primera decisión.
• Ramas: Desde el nodo inicial, dibuja ramas para cada posible resultado del evento o decisión. Etiqueta cada rama con la probabilidad correspondiente.
• Repetir para Subsecuentes Decisiones o Eventos: Para cada nuevo nodo creado en el paso anterior, repite el proceso de dibujar ramas para cada posible resultado siguiente.

Paso 3: Calcular Probabilidades

Utiliza las etiquetas de probabilidad en las ramas para calcular la probabilidad de secuencias de eventos. La probabilidad de cualquier secuencia de eventos es el producto de las probabilidades a lo largo del camino que representa esa secuencia en el diagrama.

Ejemplo de un Diagrama de Árbol: Lanzar dos monedas

Supongamos que lanzamos una moneda dos veces y queremos representar los posibles resultados.

• Nodo Raíz: Comienza el diagrama.
• Primer Lanzamiento: Dos ramas, una para Cara (C) y otra para Cruz (Z), cada una con probabilidad de 0.5.
• Segundo Lanzamiento: Desde cada uno de los nodos resultantes del primer lanzamiento, dibuja otras dos ramas, una para Cara y otra para Cruz, también cada una con probabilidad de 0.5.

¡En el navegador de la derecha podrás jugar con uno en este enlace:

Enlace al programa

Ejemplo online de evento independiente

El subprograma del enlace hay un diagrama de árbol y diez canicas azules y naranjas debajo del diagrama de árbol (es posible que deba desplazarse hacia abajo para ver las canicas). Si haces clic en una de las canicas, el diagrama de árbol se completará según lo que hayas seleccionado.

Después de seleccionar dos canicas, aparecerá una ecuación para la regla del producto encima de las canicas.

El número de canicas naranjas y azules se aleatoriza cada vez que golpeas Reset, por lo que verás muchos valores diferentes para prob1 , prob2 y final_prob .

Pruebe todos los resultados posibles y observe el diagrama de árbol en consecuencia:

Enlace al programa

Axioma 3: Probabilidad del Espacio Muestral

El tercer axioma dicta que la probabilidad del espacio muestral completo es 1. Esto se alinea con la idea de que el espacio muestral representa todos los posibles resultados de un experimento, y dado que uno de esos resultados debe ocurrir, la certeza total se representa como una probabilidad de 1.

Consecuencias de los Axiomas

A partir de estos axiomas, se pueden derivar varias propiedades importantes de la probabilidad:

• Intervalo de Probabilidad: Todo evento tiene una probabilidad que se encuentra en el intervalo \([0, 1]\), inclusivo. Esto se sigue del tercer axioma y del hecho de que ningún evento puede ser más probable que el espacio muestral completo.
• Probabilidad del Complemento: La probabilidad de que un evento no ocurra (su complemento) es 1 menos la probabilidad de que el evento ocurra.
• Probabilidad del Conjunto Vacío: La probabilidad del conjunto vacío, que representa un evento imposible, es 0. Esto es coherente con la interpretación del conjunto vacío como un evento sin resultados posibles.

Derivaciones de axiomas de probabilidad

Las derivaciones de los axiomas de probabilidad se refieren a las propiedades y reglas que se pueden inferir directamente a partir de los axiomas fundamentales de la probabilidad.

Estos axiomas, como ya se ha mencionado, son la no negatividad, la aditividad (o regla de suma para eventos disjuntos) y que la probabilidad del espacio muestral completo es 1. A partir de estos axiomas, se pueden deducir varias reglas importantes que son esenciales para el trabajo práctico en probabilidad y estadística.

1. Probabilidad del Complemento de un Evento

Una de las derivaciones más directas es la probabilidad del complemento de un evento. Si \(A\) es un evento, entonces el complemento de \(A\), denotado \(A^c\), representa la ocurrencia de \(no-A\). Utilizando los axiomas, se puede demostrar que:

\[P(A^c) = 1 - P(A)\]

Esto se deduce del hecho de que \(A\) y \(A^c\) son mutuamente excluyentes y su unión es el espacio muestral completo, cuya probabilidad es 1.

2. Probabilidad de la Unión de Eventos

Para dos eventos \(A\) y \(B\), la probabilidad de su unión puede ser expresada en términos de las probabilidades de \(A\), \(B\), y su intersección \(A ∩ B\). Esta regla se aplica incluso si \(A\) y \(B\) no son disjuntos y se deriva como sigue:

\[P(A ∪ B) = P(A) + P(B) - P(A ∩ B)\]

Esto ajusta la aditividad para el caso de eventos qsue no son mutuamente excluyentes, evitando la sobrecontabilización de la intersección de \(A\) y \(B\).

3. Subaditividad

La subaditividad se refiere a la propiedad de que la probabilidad de la unión de cualquier colección de eventos es menor o igual a la suma de sus probabilidades individuales. Para una secuencia de eventos \(A1, A2,...., An\):

Esta propiedad es particularmente útil para tratar con uniones de eventos que no son necesariamente disjuntos.

4. Probabilidad de Eventos Vacíos y Ciertos

Directamente de los axiomas, se establece que la probabilidad del conjunto vacío \({∅}\), que es un evento imposible, es 0:

\[P(∅) = 0\]

Asimismo, la probabilidad del espacio muestral completo \((Ω)\), que representa un evento seguro, es 1:

\[P(Ω) = 1\]

5. Monotonicidad

Si un evento \(A\) es un subconjunto de otro evento \(B\), entonces la probabilidad de \(A\) es menor o igual a la probabilidad de \(B\). Esto refleja la idea de que la ocurrencia de \(B\) incluye la ocurrencia de \(A\) junto con posiblemente otros resultados:

\[A ⊆ B -> P(A) ≤ P(B)\]

6. Límites de Probabilidad

Cualquier probabilidad \(P(A)\) para un evento \(A\) siempre estará en el rango de 0 a 1, inclusive. Esto se deriva del hecho de que todas las probabilidades son no negativas y que la probabilidad del espacio muestral, el conjunto más grande posible, es 1.

Analisis utilizando una Tabla de contingencia

Una tabla de contingencia en probabilidad se utiliza para organizar y mostrar las probabilidades asociadas con combinaciones de categorías de dos o más variables aleatorias. Esta herramienta es muy útil para visualizar la distribución conjunta de las variables, así como para calcular probabilidades condicionales y marginales.

Creación de una Tabla de Contingencia en Probabilidad

Para ilustrar cómo se puede usar una tabla de contingencia en un contexto de probabilidad, consideremos un ejemplo sencillo con dos variables: tipo de vehículo (auto o camión) y color (blanco o negro).

Supongamos que tenemos las siguientes probabilidades:

• La probabilidad de que un vehículo sea un auto es 0.7 y un camión 0.3.
• Dada que es un auto, la probabilidad de que sea blanco es 0.4 y negro 0.6.
• Dada que es un camión, la probabilidad de que sea blanco es 0.5 y negro 0.5.

Paso 1: Establecer las Probabilidades Conjuntas

Calculamos las probabilidades conjuntas multiplicando la probabilidad de cada tipo de vehículo por la probabilidad de cada color dado ese tipo. Por ejemplo, la probabilidad de que un vehículo sea un auto blanco se calcularía como \(0.7 \times 0.4 = 0.28\).

Paso 2: Crear la Tabla

La tabla se organiza poniendo una variable en las filas y otra en las columnas, con las probabilidades calculadas en las celdas correspondientes.

Vehículo/Color	Blanco	Negro	Total
Auto	0.28	0.42	0.7
Camión	0.15	0.15	0.3
Total	0.43	0.57	1

Análisis de la Tabla

1. Probabilidades Marginales:
   • \[P(\text{Blanco}) = 0.43\]
   • \[P(\text{Negro}) = 0.57\]
2. Probabilidades Condicionales:
   • \[P(\text{Auto} \mid \text{Blanco}) = \frac{0.28}{0.43} \approx 0.651\]
   • \[P(\text{Camión} \mid \text{Blanco}) = \frac{0.15}{0.43} \approx 0.349\]

Importancia y Usos

• Visualización de Relaciones: La tabla de contingencia muestra claramente cómo se distribuyen las probabilidades entre diferentes categorías de variables.
• Facilita el Cálculo: Permite calcular fácilmente probabilidades marginales y condicionales.
• Análisis Estadístico: Puede ser utilizada para realizar pruebas de independencia como el test de chi-cuadrado.

Tablas de contingencia como esta son extremadamente útiles en estadísticas, ciencia de datos, investigación de mercados, y muchos otros campos donde las relaciones entre variables categóricas son importantes para el análisis de decisiones y predicciones.

Ejemplos de modelos de probabilidad discretos:

Este ejemplo nos permitirá entender cómo definir un espacio muestral y cómo asignar probabilidades a los eventos dentro de ese espacio. Los modelos de probabilidad discretos se ocupan de experimentos donde el número de posibles resultados es finito o contable. Un ejemplo clásico es el lanzamiento de dados, donde los resultados posibles pueden listarse de manera explícita.

Supongamos que tenemos dos dados de cuatro caras, donde cada resultado tiene una probabilidad de \(1/16\), podemos construir una tabla que muestre todas las combinaciones posibles de los resultados de los dos dados. Cada dado puede mostrar uno de cuatro resultados posibles (1, 2, 3, o 4), lo que nos da un total de \(4 \times 4 = 16\) combinaciones posibles para los dos dados. Aquí está la tabla que modela el espacio muestral con la probabilidad asignada a cada par de resultados. Cada uno de estos nuemros deben ser positivos y la suma de todos debe ser 1.

	1	2	3	4
1	1/16	1/16	1/16	1/16
2	1/16	1/16	1/16	1/16
3	1/16	1/16	1/16	1/16
4	1/16	1/16	1/16	1/16

Cada celda representa una posibilidad de resultado:

	1	2	3	4
1	{1,1}	{1,2}	{1,3}	{1,4}
2	{2,1}	{2,2}	{2,3}	{2,4}
3	{3,1}	{3,2}	{3,3}	{3,4}
4	{4,1}	{4,2}	{4,3}	{4,4}

Una vez establecido el espacio muestral y las probabilidades, podemos investigar ciertas preguntas:

Probabilidad de Suma Par

¿Cuál es la probabilidad de que la suma de los resultados de los dos dados sea un número par? Para responder, identificamos los pares cuya suma es par y calculamos la probabilidad combinada de estos pares.

	1	2	3	4
1	2	3	4	5
2	3	4	5	6
3	4	5	6	7
4	5	6	7	8

La cantidad de celdas con valores pares es 8 asi que seria 8 * 1/16 = 1/2, asi que la probabilidad de que la suma de los resultados sea un numero par es de un 50%.

Probabilidad de que al Menos un Dado Muestre un Cuatro:

¿Cuál es la probabilidad de que al menos uno de los dados muestre un cuatro? Nuevamente, seleccionamos los pares que cumplen con esta condición y sumamos sus probabilidades. Segun nuestra tabla de espacio muestral hay 7 eventos que pueden tener 4 como resultado. Seria 7 * 1/16 = 7/16.

Ejemplo Práctico: Predicciones de Enfermedades por un Médico

Imaginemos que tenemos un médico con 20 años de experiencia que, basándose en datos históricos, ha desarrollado un modelo para predecir la probabilidad de que el próximo paciente que llegue a su clínica tenga malaria o tifoidea, o ambas enfermedades. Según este modelo:

• La probabilidad de que el próximo paciente tenga malaria es del 0.6.
• La probabilidad de que el próximo paciente tenga tifoidea es del 0.7.
• La probabilidad de que el próximo paciente tenga tanto malaria como tifoidea es del 0.4.

Con esta información, se nos plantea la pregunta:
¿Cuál es la probabilidad de que el próximo paciente no tenga ni malaria ni tifoidea?

Para calcular la probabilidad de que el próximo paciente no tenga ni malaria ni tifoidea, podemos utilizar la teoría de probabilidad de conjuntos, específicamente la ley de la probabilidad del complemento y la fórmula para la unión de dos eventos.

Leyes y Fórmulas Utilizadas

1. Probabilidad del Complemento:
   \(P(\text{no } A) = 1 - P(A)\) Esta fórmula se utiliza para encontrar la probabilidad de que un evento no ocurra, que es uno menos la probabilidad de que el evento ocurra.

2. Fórmula de la Unión de Dos Eventos: \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\) Aquí, \(P(A \cup B)\) representa la probabilidad de que ocurra al menos uno de los eventos \(A\) o \(B\), \(P(A)\) y \(P(B)\) son las probabilidades de los eventos individuales, y \(P(A \cap B)\) es la probabilidad de que ambos eventos ocurran simultáneamente.

Dado que:

• La probabilidad de tener Malaria: \(P(M) = 0.6\)
• La probabilidad de tener Tifoidea: \(P(T) = 0.7\)
• La probabilidad de tener ambos: \(P(M \cap T) = 0.4\)

Queremos calcular \(P(\text{ni malaria ni tifoidea})\), que es el complemento de la probabilidad de que el paciente tenga malaria o tifoidea. Primero, calcularemos \(P(\text{malaria} \cup \text{tifoidea})\) usando la fórmula de la unión de dos eventos:

\[P(M \cup T) = P(M) + P(T) - P(M \cap T) = 0.6 + 0.7 - 0.4 = 0.9\]

Luego, aplicaremos la probabilidad del complemento para obtener la probabilidad de que el paciente no tenga ninguna de las dos enfermedades:

\[P(\text{ni malaria ni tifoidea}) = 1 - P(M \cup T) = 1 − 0.9 = 0.1\]

Así que, basado en estos cálculos, la probabilidad de que el próximo paciente no tenga ni malaria ni tifoidea es del 10%. Si puedes acceder a un entorno de Python, simplemente puedes utilizar estos cálculos directamente para confirmar el resultado.

La probabilidad condicional

La probabilidad condicional nos indica la probabilidad de que ocurra un evento \(A\), dado que ya sabemos que otro evento \(B\) ha ocurrido. Esta se denota como \(P(A\|B)\) y se calcula usando la fórmula:

\[P(A|B) = \frac{P(A \cap B)}{P(B)}\]

donde \(P(A \cap B)\) es la probabilidad de que ocurran \(A\) y \(B\) juntos, y \(P(B)\) es la probabilidad de que ocurra \(B\).

Ejemplos Prácticos

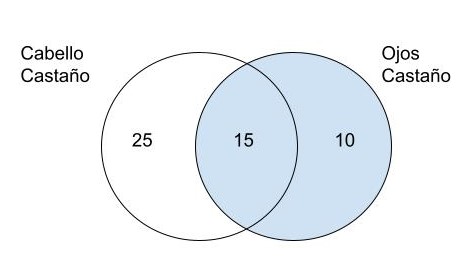
1. Ejemplo 1 En una ciudad el 40% de la poblacion tiene pelo castaño (PC), el 25% tiene ojos castaños(OC) y el 15% tiene cabellos y ojos castaños. Si se selecciona una persona al azar y esta tiene ojos castaños ¿Cual es la probabilidad de que tenga tambien cabello castaño? Formula de la probabilidad condicional:

\[P(A|B) = \frac{P(A \cap B)}{P(B)}\]

Solucion:

• Probabilidad de que tenga el cabello castaño: \(P(C) = 40\%\)
• Probabilidad de que tenga los ojos castaños: \(P(O) = 25\%\)
• Probabilidad de que tenga el cabello castaño y los ojos castaños: \(P(C \cap O) = \15%\)

Formulacion:

\[\begin{aligned} P(C|O) = \frac{P(C \cap O)}{P(O)} \\ P(C|O) = \frac{15}{25} \\ P(C|O) = \frac{0.15}{0.25} \\ P(C|O) = 0.6 = 60\% \end{aligned}\]

Resolviendo el ejercicio utilizando los diagramas de Venn, representamos la interseccion de los dos conjuntos, los de cabello castaño, los de ojos castaños. Como queremos saber la probabilidad de que al escojer una persona con los ojos castaños tenga tambien el cabello castaño, estaremos trabajando con el conjunto de las personas de ojos castaños y la interseccion con el conjunto de cabello castaño.

\[\begin{aligned} P(C|O) = \frac{15}{25} \\ P(C|O) = \frac{0.15}{0.25} \\ P(C|O) = 0.6 = 60\% \end{aligned}\]

Imaginemos que tenemos un dado de seis caras que está cargado de tal manera que los números pares tienen el doble de probabilidades de salir que los números impares. Si definimos dos eventos:

• \(A\): Sacar un número no mayor que 4: \(A = \{1, 2, 3, 4\}\).
• \(B\): Sacar un número par: \(B = \{2, 4, 6\}\).

Dado que los números pares tienen el doble de probabilidades de salir que los números impares y que todos los números pares entre sí son igualmente probables, así como todos los números impares entre sí, podemos establecer lo siguiente:

• Las probabilidades de sacar un número par \(P(E2) = P(E4) = P(E6) = x\) es el doble que la de sacar un número impar \(P(E1) = P(E3) = P(E5) = y\), por lo que \(x = 2y\).
• Teniendo en cuenta que el dado es de seis caras y todas las probabilidades deben sumar 1, tenemos \(3x + 3y = 1\).

Sustituyendo \(x\) por \(2y\) en la ecuación \(3x + 3y = 1\), obtenemos \(3(2y) + 3y = 1\), lo que simplifica a \(6y + 3y = 1\), dando \(9y = 1\). De aquí, podemos resolver \(y = \frac{1}{9}\).

Como \(x = 2y\), entonces \(x = \frac{2}{9}\).

Esto significa que las probabilidades para cada resultado son:

• Para números impares \((1, 3, 5)\): \(y = \frac{1}{9}\).
• Para números pares \((2, 4, 6)\): \(x = \frac{2}{9}\).

Ahora, para calcular la probabilidad de \(P(A)\) (sacar un número no mayor que 4), sumamos las probabilidades de los resultados individuales en \(A\):

\[\begin{aligned} P(A) = P(E1) + P(E2) + P(E3) + P(E4) \\ P(A) = \frac{1}{9} + \frac{2}{9} + \frac{1}{9} + \frac{2}{9} \\ P(A) = \frac{6}{9} \\ P(A) = \frac{2}{3} \end{aligned}\]

Por lo tanto, la probabilidad de sacar un número no mayor que 4 con este dado cargado es de \(\frac{2}{3}\).

4. Cálculo de la Probabilidad Condicional en el Ejemplo

Para calcular \(P(A\|B)\), primero identificamos la intersección de \(A\) y \(B\), que es \(A ∩ B = \{2, 4\}\), cuyas probabilidades suman \(4/9\). Normalizamos esta suma con la probabilidad de \(B\), (2/3), obteniendo:

\[P(A|B) = \frac{4/9}{2/3} = \frac{4/9}{6/9} = \frac{4}{6} = \frac{2}{3}\]

Este resultado nos indica que, sabiendo que el resultado será un número par, la probabilidad de que también sea un número no mayor a 4 es \(2/3\), igual que la probabilidad de \(A\) sin condicionar. Esto demuestra la independencia de \(A\) respecto a \(B\).

Probabilidad condicional en el aprendizaje automático

En el mundo del aprendizaje automático, la probabilidad condicional juega un papel crucial, siendo la base sobre la cual se construyen la mayoría de los modelos.

Aplicaciones en el Aprendizaje Automático

El aprendizaje automático utiliza extensivamente la probabilidad condicional para modelar y predecir resultados basándose en datos históricos o condiciones previas. Veamos algunos ejemplos:

• Reconocimiento Facial: Imagina una cámara que desbloquea una puerta si reconoce a una persona autorizada. Aquí, la probabilidad condicional nos ayuda a predecir la probabilidad de que la persona frente a la cámara sea, de hecho, un empleado autorizado, basándose en la imagen capturada.

• Reconocimiento de Actividades en Videos: Al analizar un video, podemos querer identificar qué actividad se está realizando. Utilizamos variables aleatorias para representar tanto la actividad como los datos del video, y mediante la probabilidad condicional, modelamos la probabilidad de que se esté realizando una actividad específica.

• Sistemas de Reconocimiento de Voz a Texto: Aquí, la probabilidad condicional se usa para modelar la probabilidad de que ciertas palabras o frases sean dichas, basándose en los sonidos capturados.

Probabilidad condicional en la Ley de Probabilidad Total

La Ley de Probabilidad Total, un concepto fundamental en la teoría de probabilidad que nos permite calcular la probabilidad de un evento a partir de la suma de las probabilidades de varios eventos mutuamente excluyentes que forman una partición del espacio muestral.

Para definir la Ley de la Probabilidad Total, Consideremos un espacio muestral \(\Omega\) dividido en varios eventos mutuamente excluyentes \(A_1, A_2, ..., A_n\) que forman una partición de \(\Omega\). Esto significa que cada elemento de \(\Omega\) pertenece exactamente a uno de los eventos \(A_i\) y la unión de todos los \(A_i\) recupera el espacio muestral completo. La Ley de Probabilidad Total nos dice que para cualquier evento \(B\), la probabilidad de \(B\) se puede expresar como:

\[P(B) = P(B \cap A_1) + P(B \cap A_2) + ... + P(B \cap A_n)\]

Para ilustrar, imagina que tenemos un espacio muestral representado por un conjunto \(\Omega\), y este espacio se divide en 4 partes \(A_1, A_2, A_3\) y \(A_4\), formando una partición completa de \(\Omega\). Supongamos que tenemos un evento \(B\) que ocurre dentro de este espacio. La probabilidad de \(B\) se puede calcular considerando sus intersecciones con cada uno de los conjuntos \(A_i\).

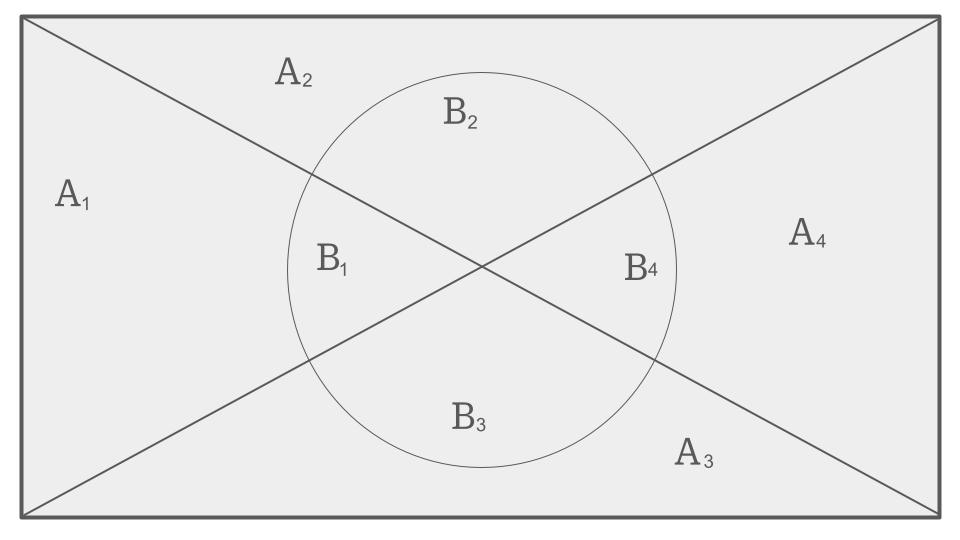
Esta ley es especialmente útil cuando trabajamos con variables aleatorias que representan datos reales. A menudo, nos encontramos con distribuciones conjuntas que involucran varias variables aleatorias y deseamos calcular distribuciones marginales. La Ley de Probabilidad Total nos proporciona una forma de hacerlo, sumando las probabilidades de eventos que están condicionados por las particiones del espacio muestral.

Independencia de los modelos de probabilidad

La independencia, también conocida como independencia estadística, es una propiedad clave entre dos o más eventos en la teoría de la probabilidad. Dos eventos, \(A\) y \(B\), se consideran independientes si la ocurrencia de uno no afecta la probabilidad de ocurrencia del otro. Matemáticamente, esto se expresa como:

\[P(A \cap B) = P(A) \times P(B)\]

donde \(P(A \cap B)\) es la probabilidad de que ambos eventos sucedan simultáneamente, y \(P(A)\) y \(P(B)\) son las probabilidades de que cada evento suceda independientemente.

Ejemplos de Independencia

1. Lanzamiento de una moneda y un dado: Supongamos que lanzamos una moneda y un dado al mismo tiempo. La probabilidad de que la moneda muestre cara \(P(cara) = \frac{1}{2}\), y la probabilidad de que el dado muestre un seis \(P(B_6) = \frac{1}{6}\). Estos dos eventos son independientes porque el resultado de la moneda no influye en el resultado del dado, entonces:

\[P(A \cap B) = P(A) \times P(B) = \frac{1}{2} \times \frac{1}{6} = \frac{1}{12}\]

1. Elegir cartas de diferentes barajas: Si eliges una carta de una baraja y otra de una baraja diferente, estos dos eventos son independientes porque el resultado de una elección no afecta el resultado de la otra.

Profundización en la Independencia Mutua

La pregunta central en la transcripción es si la independencia es mutua; es decir, si \(A\) es independiente de \(B\), ¿implica esto que \(B\) también es independiente de \(A\)? La respuesta es sí, porque la independencia entre dos eventos es siempre mutua dado que la relación matemática no cambia al invertir los roles.

Independencia en Conjuntos de Más de Dos Eventos

Cuando tratamos con más de dos eventos, establecer la independencia se vuelve más complejo. Para que tres eventos, por ejemplo, \(A\), \(B\), y \(C\), sean mutuamente independientes, deben cumplir todas las siguientes condiciones:

• \[P(A \cap B \cap C) = P(A) \times P(B) \times P(C)\]
• \[P(A \cap B) = P(A) \times P(B)\]
• \[P(A \cap C) = P(A) \times P(C)\]
• \[P(B \cap C) = P(B) \times P(C)\]

Estas condiciones garantizan que la independencia se mantiene en todos los subconjuntos de eventos.

Modelos de probabilidad de Independencia condicional

La independencia condicional es un concepto más refinado que indica que dos eventos pueden ser independientes bajo la condición de un tercer evento. Matemáticamente, dos eventos \(A\) y \(B\) son condicionalmente independientes dado un tercer evento \(C\) si:

\[P(A \cap B | C) = P(A | C) \times P(B | C)\]

Este concepto es crucial en contextos donde la independencia absoluta no se mantiene, pero se establece una vez que se considera un evento condicionante.

Ejemplo de Independencia Condicional

Considera el caso de testear un software bajo diferentes condiciones de red. Dos fallos distintos, \(A\) y \(B\), pueden no ser independientes en general (es decir, que uno ocurra puede afectar la probabilidad del otro), pero si condicionamos al tipo de red \(C\) (por ejemplo, 4G vs. WiFi), estos fallos pueden volverse independientes dentro de cada tipo de red.

Regla de Bayes

El Teorema de Bayes, nombrado así por el reverendo Thomas Bayes, es un principio fundamental en la teoría de la probabilidad que permite actualizar la probabilidad de un evento basado en nueva evidencia o información. Este teorema es esencial para el razonamiento estadístico y se utiliza en una amplia variedad de campos, desde la inteligencia artificial hasta la epidemiología.

Fórmula del Teorema de Bayes

La fórmula del Teorema de Bayes relaciona las probabilidades condicionales e incondicionales de eventos estadísticos. Se expresa matemáticamente como:

\[P(A \mid B) = \frac{P(B \mid A) \times P(A)}{P(B)}\]

Donde:

• \(P(A \mid B)\) es la probabilidad posterior de \(A\) dado \(B\), o la probabilidad de \(A\) después de haber observado \(B\).
• \(P(B \mid A)\) es la probabilidad de observar \(B\) dado que \(A\) es verdadero.
• \(P(A)\) es la probabilidad a priori de \(A\), o la probabilidad de \(A\) antes de observar \(B\).
• \(P(B)\) es la probabilidad total de \(B\), que se calcula utilizando la ley de probabilidad total.

Entendiendo las Partes del Teorema

• Probabilidad a Priori \(P(A)\): Es la probabilidad inicial de \(A\) antes de que se tenga en cuenta cualquier información adicional.
• Probabilidad Condicional \(P(B \mid A)\): Es la probabilidad de observar \(B\) cuando \(A\) es cierto.
• Probabilidad a Posteriori \(P(A \mid B)\): Es la probabilidad revisada de \(A\) después de tener en cuenta la evidencia \(B\).

• Probabilidad Marginal \(P(B)\): También conocida como la probabilidad total de \(B\), esta es la suma de las probabilidades de \(B\) sobre todos los posibles resultados anteriores. Se calcula como:

  \[P(B) = P(B \mid A) \times P(A) + P(B \mid A^c) \times P(A^c)\]

  donde \(A^c\) es el complemento de \(A\).

Ejemplo de Aplicación

Para este problema, seguiremos el diagrama de árbol:

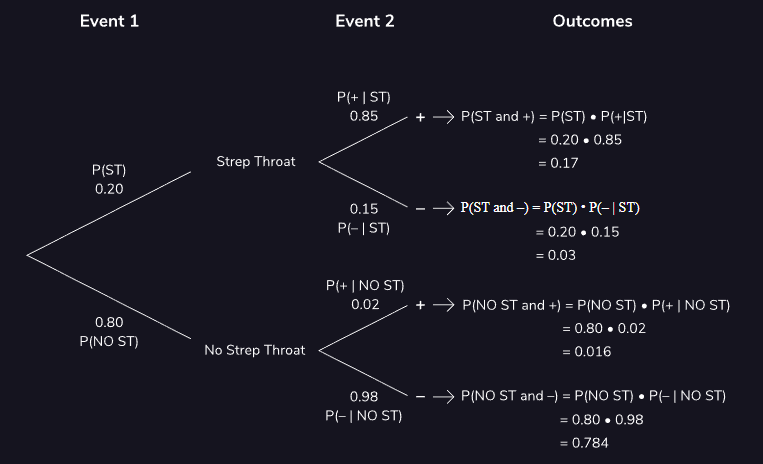
Supongamos que lo siguiente es cierto (esto se muestra en el primer conjunto de ramas del diagrama):

• El 20 por ciento de la población tiene faringitis estreptocócica: \(P(ST) = 0.20\)
• El 80 por ciento de la población no tiene faringitis estreptocócica: \(P(No ST) = 0.80\)

Ahora supongamos que hacemos pruebas a un grupo de personas para detectar faringitis estreptocócica. Los posibles resultados de estas pruebas se muestran en el siguiente conjunto de ramas:

• Si una persona tiene faringitis estreptocócica, hay un 85% de posibilidades de que su prueba sea positiva y un 15% de posibilidades de que sea negativa. Esto está etiquetado como:

• Test Positivo: P(+|ST) = 0.85
• Test Negativo: P(-|ST) = 0.15

Por otra parte:

• Si una persona NO tiene faringitis estreptocócica, hay un 2% de posibilidades de que su prueba sea positiva y un 98% de posibilidades de que sea negativa. Esto está etiquetado como:

• Test Positivo: P(+|No ST) = 0.02
• Test Negativo: P(-|No ST) = 0.98

Finalmente, veamos los cuatro posibles pares de resultados que forman las ramas terminales de nuestro diagrama:

• \[P(ST y + ) = 0.17\]
• \[P(ST y - ) = 0.03\]
• \[P(No ST y +) = 0.016\]
• \(P(No ST y -) = 0.784\)
  ​

En conjunto, estos suman uno, ya que capturan todos los resultados potenciales después de que se realizan las pruebas a los pacientes.

Es genial que tengamos toda esta información. Sin embargo, nos falta algo. Si alguien obtiene un resultado positivo, ¿cuál es la probabilidad de que este correcto el test y realmente tenga faringitis estreptocócica? Notacionalmente, podemos escribir esta probabilidad como: \(P(ST\|+)\)

Imagine que es un paciente que recientemente dio positivo por faringitis estreptocócica. Es posible que desee saber la probabilidad de que TIENE faringitis estreptocócica, dado que su prueba dio positivo. Para calcular esta probabilidad, el Teorema de Bayes , que establece lo siguiente:

\[P(A \mid B) = \frac{P(B \mid A) \times P(A)}{P(B)}\]

Calculando

\[\begin{aligned} P(ST\|+) = \frac{P(+\|ST) \times P(ST)}{P(+)} \\ P(ST\|+) = \frac{0,85 \times 0,20}{P(+)} \\ \end{aligned}\]

Qué pasa con P(+) ? ¿Es esto algo que sabemos? Bueno, pensemos en esto. Hay cuatro resultados posibles: ​

• Tener faringitis estreptocócica y dar positivo
• Tener faringitis estreptocócica y dar negativo
• No tener faringitis estreptocócica y dar positivo
• No tener faringitis estreptocócica y dar negativo

Solo nos importan los dos resultados en los que un paciente da positivo en \(P(+)\) . Por tanto, podemos decir:

\[\begin{aligned} P(+) = P(ST y +) + P(No ST y +) \\ P(+) = 0,17 + 0,16 \\ P(+) = 0,186 \\ \end{aligned}\]

Continuamos con la formula principal:

\[\begin{aligned} P(ST\|+) = \frac{P(+\|ST) \times P(ST)}{P(+)} \\ P(ST\|+) = \frac{0,85 \times 0,20}{0,186} \\ P(ST\|+) = 0.914 \end{aligned}\]

Existe un 91,4% de posibilidades de que realmente tenga faringitis estreptocócica si su prueba da positivo. Esto no es obvio a partir de la información descrita en nuestro diagrama de árbol, pero con el poder del teorema de Bayes, pudimos calcularlo.

Podemos calcular otras probabilidades condicionales como, \(P(ST\|-), P(NoST\|+), P(NoST\|-)\).

Aplicaciones en el Aprendizaje Automático

La Regla de Bayes es la base del clasificador Bayesiano, un algoritmo de aprendizaje automático que clasifica los datos basándose en la probabilidad de que pertenezcan a una clase dada la observación de sus características. Este clasificador se utiliza en:

• Filtros de spam en correos electrónicos.
• Clasificación de documentos y textos.
• Diagnósticos médicos automáticos.

Modelo Generativo vs. Modelo Discriminativo

La distinción entre modelado generativo y discriminativo es fundamental en el aprendizaje automático:

• Modelo Generativo: Intenta modelar cómo se generan los datos, combinando las distribuciones de las características y las clases. Ejemplos incluyen el clasificador Bayesiano y la mezcla de modelos Gaussianos.
• Modelo Discriminativo: Se enfoca en la frontera entre las clases, intentando directamente predecir la clase a partir de las características observadas. Ejemplos incluyen la regresión logística y las máquinas de soporte vectorial (SVM).

Proyecto: crear un Clasificador de Bayes desde cero

Para el proyecto utilizaremos el conjunto de datos iris de la biblioteca `seaborn. El conjunto de datos Iris contiene mediciones de 150 flores de iris, específicamente sus longitudes y anchuras de pétalos y sépalos. Cada flor es clasificada en una de tres especies: Setosa, Versicolor o Virginica. La carga de datos se realiza típicamente con bibliotecas como Seaborn, que facilita la visualización y manipulación de datos: