Expectativa
El concepto de expectativa (o valor esperado) es fundamental en el campo de la probabilidad y estadísticas. La expectativa proporciona un resumen numérico central de una variable aleatoria, ofreciendo una medida de la “tendencia central” o el promedio a largo plazo que uno puede esperar en una serie de experimentos donde la variable aleatoria se observa repetidamente.
La expectativa de una variable aleatoria \(X\), denotada como \(E[X]\) o \(\mu\), es el promedio ponderado de todos los posibles valores que \(X\) puede tomar, ponderados por la probabilidad de cada valor. Matemáticamente se define de diferentes maneras dependiendo de si la variable aleatoria es discreta o continua:
-
Variable Discreta: Si \(X\) es una variable aleatoria discreta que toma valores \((x_1, x_2, x_3, \dots)\) con probabilidades \((p_1, p_2, p_3, \dots)\), entonces el valor esperado de \(X\) se calcula como:
\[E[X] = \sum_{i} x_i p_i\]donde la suma se extiende sobre todos los valores posibles de \(X\).
Ejemplo: Calcularemos la expectativa de una variable aleatoria que sigue una distribución binomial, donde \(𝑛 = 10\) (número de ensayos) y \(𝑝 = 0.5\) (probabilidad de éxito en cada ensayo).
import scipy.stats as stats
# Parámetros de la distribución binomial
n = 10 # número de ensayos
p = 0.5 # probabilidad de éxito
# Crear una variable aleatoria binomial
binomial_var = stats.binom(n, p)
# Calcular la expectativa
expected_value = binomial_var.mean()
print("Expectativa de la variable binomial:", expected_value)
-
Variable Continua: Si \(X\) es una variable aleatoria continua con una función de densidad de probabilidad (PDF) \(f(x)\), el valor esperado se define como:
\[E[X] = \int_{-\infty}^{\infty} x f(x) \, dx\]donde la integral se evalúa sobre todo el rango de \(X\).
Ejemplo: Calcular la expectativa de una variable aleatoria que sigue una distribución normal, con media \(𝜇 = 0\) y desviación estándar \(𝜎 = 1\).
# Parámetros de la distribución normal
mu = 0 # media
sigma = 1 # desviación estándar
# Crear una variable aleatoria normal
normal_var = stats.norm(mu, sigma)
# Calcular la expectativa
expected_value = normal_var.mean()
print("Expectativa de la variable normal:", expected_value)
Generalizando el Cálculo de la Expectativa
Para otras distribuciones, puedes seguir un procedimiento similar utilizando las funciones proporcionadas por SciPy para esa distribución específica. Aquí está cómo se haría de forma general:
# Para una distribución general, reemplazar 'dist' con el nombre de la distribución
# y configurar sus parámetros específicos.
dist_var = stats.dist(param1, param2, ...)
# Calcular la expectativa
expected_value = dist_var.mean()
print("Expectativa de la distribución:", expected_value)
Ley de los Grandes Numeros
La Ley de los Grandes Números (LLN) es un teorema fundamental en teoría de la probabilidad que describe el resultado de realizar el mismo experimento un gran número de veces. Según la LLN, el promedio de los resultados obtenidos de un gran número de pruebas se acercará al valor esperado a medida que se incremente el número de pruebas. Esto implica que las frecuencias relativas de los resultados convergen a las probabilidades teóricas.
LLN Débil vs. LLN Fuerte
-
LLN Débil: Asegura que, para cualquier tolerancia \(\epsilon > 0\), la probabilidad de que el promedio de las muestras difiera del valor esperado por más de \(\epsilon\) tiende a cero conforme el tamaño de la muestra se hace infinitamente grande.
-
LLN Fuerte: Establece que con probabilidad 1, el promedio de las muestras converge al valor esperado cuando el tamaño de la muestra tiende a infinito.
Simulaciones Estadísticas en Python
Generación de Datos
Usaremos Python para simular datos utilizando módulos como numpy y scipy. Por ejemplo, para simular una variable aleatoria binomial, podemos usar el siguiente código:
import numpy as np
# Simular 1000 ensayos de una distribución binomial con n=10 y p=0.5
data = np.random.binomial(10, 0.5, 1000)
Cálculo de Promedios
Para calcular el promedio de los datos simulados y compararlos con el valor esperado:
average = np.mean(data)
print("Promedio calculado:", average)
Análisis de Datos y Estimación de Parámetros
-
Interpretación de Resultados: Los resultados de las simulaciones deben interpretarse en el contexto de la LLN. Por ejemplo, si el promedio calculado de los ensayos binomiales difiere significativamente del valor esperado (5 en este caso), se debería aumentar el número de ensayos.
-
Estimación de Parámetros: La estimación de parámetros puede mejorar utilizando métodos como el de Máxima Verosimilitud o los Métodos de Momentos. Esto permite ajustar los parámetros de la distribución a partir de los datos observados para que coincidan más estrechamente con el valor teórico esperado.
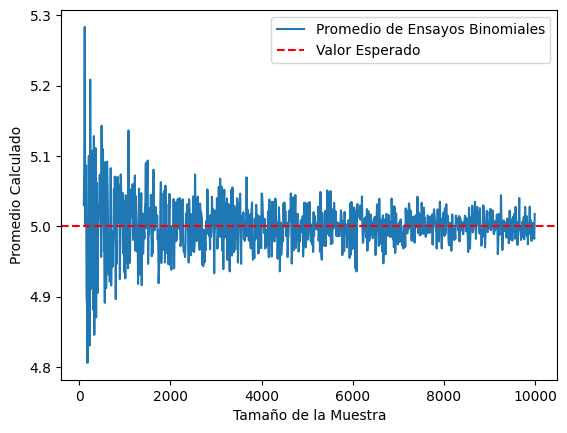
import matplotlib.pyplot as plt
import numpy as np
# Simular progresivamente mayores cantidades de ensayos
sample_sizes = np.arange(100, 10000, 10)
averages = [np.mean(np.random.binomial(10, 0.5, size)) for size in sample_sizes]
# Graficar los resultados
plt.plot(sample_sizes, averages, label="Promedio de Ensayos Binomiales")
plt.axhline(y=5, color='r', linestyle='--', label="Valor Esperado")
plt.xlabel("Tamaño de la Muestra")
plt.ylabel("Promedio Calculado")
plt.legend()
plt.show()
Independencia y Distribución Idéntica de las Muestras (IID)
Datos independientes e idénticamente distribuidos (IID) son aquellos donde cada dato en una muestra es generado de manera independiente de los otros y todos siguen exactamente la misma distribución de probabilidad. Esta propiedad es esencial para aplicar correctamente la Ley de los Grandes Números.
En contextos experimentales, garantizar que los datos son IID implica diseñar experimentos donde las intervenciones externas o las condiciones previas no afectan los resultados de cada prueba. Por ejemplo, en ensayos clínicos, los sujetos deben ser asignados aleatoriamente a grupos de tratamiento para asegurar la independencia.
Relación entre Muestras y la Población
-
Media de la Población vs. Media de la Muestra: La media de la población es el valor promedio de un parámetro en toda la población, mientras que la media de la muestra se calcula de la misma manera pero solo utilizando una parte de la población. La Ley de los Grandes Números asegura que estas dos medias converjan a medida que el tamaño de la muestra aumenta.
-
Estimación de Parámetros: La estimación de parámetros se realiza utilizando la media de la muestra y otras estadísticas para hacer inferencias sobre la población total. Esto es fundamental en áreas como la demografía y la investigación de mercado, donde no es práctico estudiar a toda la población.
Ejemplos de Variables Aleatorias y sus Expectativas
Variables Discretas Comunes:
- Bernoulli: Eventos de éxito/fallo; la expectativa es \(p\).
- Binomial: Número de éxitos en \(n\) ensayos de Bernoulli; expectativa \(np\).
- Geométrica: Número de ensayos hasta el primer éxito; expectativa \(1/p\).
- Poisson: Número de eventos en un intervalo fijo; expectativa \(\lambda\).
Variables Continuas Comunes:
- Normal (Gaussiana): Distribuida simétricamente alrededor de la media; la expectativa es \(\mu\).
- Exponencial: Tiempo entre eventos en un proceso de Poisson; expectativa \(1/\lambda\).
Momentos
Los momentos son medidas que capturan características importantes sobre la forma de una distribución de probabilidad. Estos incluyen la tendencia central, la dispersión y la forma de la distribución. Los momentos se definen generalmente respecto al origen o respecto a la media de la distribución, y cada uno de ellos ofrece información específica sobre la distribución.
Momentos Respecto al Origen
Los momentos respecto al origen se calculan como el valor esperado de las potencias sucesivas de la variable aleatoria \(X\). Matemáticamente, el \(k\)-ésimo momento respecto al origen de una variable aleatoria \(X\) se define como:
\[\mu'_k = E[X^k]\]donde \(E[\cdot]\) denota el valor esperado y \(k\) es un entero no negativo.
Momentos Centrales
Los momentos centrales, por otro lado, se calculan respecto a la media de la distribución y proporcionan información sobre la variabilidad y la forma de la distribución más allá de la media. El \(k\)-ésimo momento central se define como:
\[\mu_k = E[(X - E[X])^k]\]Tipos de Momentos y su Significado
- Primer Momento (Media):
- El primer momento respecto al origen es simplemente la media de la distribución, \(E[X]\).
- Este momento mide la tendencia central de la distribución.
- Segundo Momento (Varianza):
- El segundo momento central, conocido como la varianza, \(\text{Var}(X) = E[(X - E[X])^2]\), mide la dispersión de la distribución alrededor de su media.
- Cuanto mayor es la varianza, más dispersos están los datos alrededor de la media.
- Tercer Momento (Asimetría):
- El tercer momento central está relacionado con la asimetría (skewness) de la distribución.
- Una asimetría positiva indica una distribución con una cola más larga hacia la derecha; una negativa indica una cola más larga hacia la izquierda.
- Cuarto Momento (Curtosis):
- El cuarto momento central se relaciona con la curtosis, que mide la “altitud” y la “anchura” de las colas de la distribución.
- La curtosis compara la cantidad de datos en las colas con la cantidad de datos cerca de la media, proporcionando una percepción de la forma general de la distribución.
Los momentos son fundamentales en estadística porque permiten describir y comparar distribuciones de manera cuantitativa. Son esenciales en muchas aplicaciones estadísticas, incluyendo el ajuste de modelos, pruebas de hipótesis y en el desarrollo de teoremas centrales como el Teorema del Límite Central. Además, los momentos son cruciales para entender propiedades de distribuciones teóricas como la normal, la binomial, y otras distribuciones comunes en estudios estadísticos.
Varianza
Transformación de Variables Aleatorias
Una variable aleatoria transformada surge cuando se aplica una función a una variable aleatoria. Ejemplo de transformación: \(Y = 3X^2 + 9\), donde \(X\) es la variable aleatoria original y \(Y\) es la nueva variable.
Varianza y sus Implicaciones
- Definición y Cálculo:
- La varianza \(\text{Var}(X)\) es el valor esperado de la desviación cuadrada desde la media: \(\text{Var}(X) = E[(X - E[X])^2]\).
- Para una distribución normal, la varianza se denota como ( \sigma^2 ).
- Interpretación:
- Una alta varianza indica una amplia dispersión de los puntos de datos alrededor de la media, sugiriendo valores de datos diversos.
- En el contexto de las distribuciones normales, entender la varianza es crucial para comprender la dispersión general de la distribución.
- Relevancia Estadística:
- A diferencia de la media, la ley de los grandes números no se aplica a la varianza, lo que significa que las varianzas de muestras pueden no converger a la varianza de la población sin suposiciones o correcciones adicionales.