Conjuntos (sets)
- Definicion y creacion
- Tipos de conjuntos
- Subconjuntos
- Power Sets
- Universal Sets
- Operaciones de Cojnuntos
- Leyes de Morgan
- Venn Diagrams Operations
Definicion y creacion
Un conjunto es una colección desordenada de objetos distintos. En Python se define como una colección no ordenada de elementos únicos e inmutables.
Un conjunto es básicamente una colección, tiene muchos objetos dentro y eso es una colección, pero la colección tiene cierto tipo de propiedades.
- Desordenados: Los elementos en un set no tienen un orden específico.
- Elementos Únicos: Cada elemento en un set debe ser único; no se permiten duplicados.
- Inmutables: Los elementos de un set deben ser de tipo inmutable, como números, cadenas y tuplas. No puedes incluir listas o diccionarios como elementos de un set debido a su mutabilidad.
- Iterables: Los sets en Python son iterables, lo que significa que puedes recorrer sus elementos utilizando un bucle for.
- Almacena cualquier tipo de objeto.
Para definir un conjunto en Python, puedes usar llaves {} con elementos separados por comas dentro de ellas, o bien, puedes usar la función set() para crear un conjunto, opcionalmente pasando un iterable (como una lista o tupla) desde el cual se crearán los elementos del conjunto. Aquí tienes ejemplos de ambas maneras:
# Crear un conjunto con llaves
mi_conjunto = {1, 2, 3, 4}
print(mi_conjunto) # Salida: {1, 2, 3, 4}
# Crear un conjunto vacío (debes usar set(), no {})
conjunto_vacio = set()
print(conjunto_vacio) # Salida: set()
# Crear un conjunto a partir de una lista
mi_conjunto = set([1, 2, 3, 4])
print(mi_conjunto) # Salida: {1, 2, 3, 4}
# También puedes pasar una tupla o incluso una cadena de texto
mi_conjunto_desde_tupla = set((5, 6, 7))
print(mi_conjunto_desde_tupla) # Salida: {5, 6, 7}
mi_conjunto_desde_cadena = set("hola")
print(mi_conjunto_desde_cadena) # Salida: {'h', 'o', 'a', 'l'}
Además, los conjuntos automáticamente eliminarán los duplicados de los elementos proporcionados:
# Los duplicados se eliminarán automáticamente
mi_conjunto_con_duplicados = {1, 2, 2, 3, 4, 4, 4}
print(mi_conjunto_con_duplicados) # Salida: {1, 2, 3, 4}
Cardinalidad de un conjunto
En cardinalidad, hablamos de un elemento de un conjunto o, a veces, de un miembro de un conjunto. Definamos algún conjunto de numeros como ejemplo. Aunque pueden ser cualquier tipo de objeto como ya lo definimos.
A = {1, 2, 5, 7}
Cada numero seria un elemento diferente en el conjunto. Puedes llamarlo elemento, o miembro. El símbolo griego \(∈\) se usa para denotar la relación de membresía a un conjunto. Se puede expresar que 1 es elemento de \(A\) de esta manera \(1∈A\). De forma contraria \(∉\) expresa que el elemento no pertenece al conjunto: \(4∉A\).
La cardinalidad de un conjunto se refiere al número de elementos que contiene el conjunto. En matemáticas y teoría de conjuntos, la cardinalidad puede ser finita o infinita. Un conjunto con una cantidad limitada de elementos tiene una cardinalidad finita, mientras que un conjunto que contiene una cantidad infinita de elementos tiene una cardinalidad infinita.
Cardinalidad Finita
La cardinalidad de un conjunto finito se denota como \(\|A\|\), donde \(A\) es el conjunto. Por ejemplo, si tenemos un conjunto \(A={2,4,6,8}\), la cardinalidad de \(A\) es \(4\), porque hay cuatro elementos en el conjunto. Se escribe como \(\|A\| = 4\).
Cardinalidad Infinita
Los conjuntos infinitos pueden ser contablemente infinitos o incontablemente infinitos. Un conjunto es contablemente infinito si sus elementos pueden ser contados uno por uno y asignados a los números naturales, como el conjunto de todos los números enteros. Un conjunto es incontablemente infinito si su tamaño es mayor que el conjunto de todos los números naturales, como el conjunto de todos los números reales entre 0 y 1.
Cardinalidad en Python
En Python, la cardinalidad de un conjunto se puede obtener utilizando la función len(). Por ejemplo:
mi_conjunto = {2, 4, 6, 8}
print(len(mi_conjunto))
Esto imprimirá 4, que es la cantidad de elementos en mi_conjunto.
También existen otras categorías de conjuntos finitos e infinitos. Los términos “contable” y “no contable” se utilizan para describir el tamaño de conjuntos infinitos. Estos conceptos son fundamentales para entender diferentes tipos de infinitos y cómo se pueden comparar entre sí.
Tipos de Conjuntos
Conjuntos Contables
Un conjunto se dice que es contable si sus elementos se pueden contar uno por uno, si es un objeto listable, si puedes generar una secuencia de los elementos del set. Los conjuntos contables pueden ser finitos o infinitos. Más formalmente, un conjunto es contable si se puede establecer una correspondencia uno a uno (biyección) entre los elementos del conjunto y los números naturales (0, 1, 2, 3, …). Esto significa que, incluso si el conjunto es infinito, sus elementos se pueden enumerar.
Ejemplos:
- El conjunto de todos los números enteros \(\mathbb{Z}\): En matemáticas, el conjunto de todos los números enteros se denota comúnmente con la letra \(\mathbb{Z}\). Este conjunto incluye todos los números enteros positivos y negativos, así como el cero. Es decir, \(\mathbb{Z}\) consiste en:
- El conjunto de todos los números racionales \(\mathbb{Q}\) (fracciones de enteros) es contable: El conjunto de todos los números racionales, denotado como \(\mathbb{Q}\), es el conjunto que incluye todos los números que pueden ser expresados como el cociente \(\frac{a}{b}\), donde \(a\) y \(b\) son números enteros y \(b \neq 0\). En otras palabras, un número es racional si puede ser expresado como la fracción de dos números enteros, con el denominador diferente de cero.
Conjuntos No Contables
Un conjunto se dice que es no contable si es infinito y no se puede establecer una correspondencia uno a uno con los números naturales, Un ejemplo clásico de un conjunto que es no contable es el conjunto de los números reales \(\mathbb{R}\). Este conjunto incluye todos los números racionales e irracionales en la línea numérica, extendiéndose desde \(-\infty\) hasta \(+\infty\).
Un ejemplo específico de un conjunto no contable, además del conjunto de todos los números reales \(\mathbb{R}\), es el conjunto de los números reales entre 0 y 1, también conocido como el intervalo unitario \([0, 1]\).
Este conjunto incluye todos los números reales \(x\) tal que \(0 \leq x \leq 1\). Aunque parece ser solo una pequeña parte de la línea numérica, este intervalo contiene infinitos números y es tan grande como el conjunto de todos los números reales en términos de cardinalidad.
Números Irracionales: Números que no pueden ser expresados como fracciones de enteros. Incluyen los números que tienen expansiones decimales infinitas no periódicas, como \(\pi \) y \( \sqrt{2}\).
Subconjuntos
En matemáticas, el concepto de subconjunto es fundamental en la teoría de conjuntos. Un subconjunto se refiere a una colección de elementos que son todos parte de otro conjunto, conocido como el conjunto superior o conjunto contenedor. La relación de subconjunto se define de manera que, si todos los elementos de un conjunto \(A\) también pertenecen a un conjunto \(B\), entonces \(A\) es un subconjunto de \(B\), lo cual se denota como \(A ⊆ B\).
Propiedades de los Subconjuntos
-
Subconjunto Propio: Un subconjunto \(A\) de \(B\) se considera un subconjunto propio (o estricto) si \(A\) no es igual a \(B\), es decir, si hay al menos un elemento en \(B\) que no está en \(A\). Esto se denota como \(A ⊂ B\).
-
Subconjunto Impropio: Cualquier conjunto es un subconjunto de sí mismo, \(A ⊆ A\), lo que se conoce como subconjunto impropio.
-
Subconjunto Vacío: El conjunto vacío (denotado como \(\{∅\}\) es un subconjunto de cualquier conjunto, ya que la definición de subconjunto se cumple trivialmente (no hay elementos en el conjunto vacío que no estén en el otro conjunto).
Ejemplos de Subconjuntos
- Si tenemos el conjunto \(B = {1, 2, 3, 4}\), entonces \(A = {2, 3}\) es un subconjunto de \(B\) porque todos los elementos de \(A\) también pertenecen a \(B\).
- El conjunto \(C = {1, 2, 3, 4}\) también es un subconjunto de \(B\), pero es un subconjunto impropio porque \(C\) es igual a \(B\).
Operaciones y Términos Relacionados
- Intersección: La intersección de dos conjuntos contiene solo los elementos que son comunes a ambos. Si la intersección de dos conjuntos es igual a uno de ellos, entonces ese conjunto es un subconjunto del otro.
- Unión: La unión de dos o más conjuntos contiene todos los elementos que pertenecen a cualquiera de los conjuntos. Un conjunto es un subconjunto de la unión de él mismo con cualquier otro conjunto.
- Complemento: El complemento de un conjunto \(A\) dentro de un conjunto universal
Ucontiene todos los elementos de \(U\) que no están en \(A\). Por definición, \(A\) y su complemento son subconjuntos de \(U\).
Power Sets
El conjunto potencia o power set de un conjunto dado es el conjunto de todos los subconjuntos posibles de ese conjunto, incluyendo el conjunto vacío y el conjunto mismo. Si el conjunto original se denota como \(S\), entonces su conjunto potencia se denota como \(2^S\) o \(P(S)\).
Propiedades
-
Cardinalidad: Si el conjunto original \(A\) tiene \(n\) elementos, entonces el conjunto potencia de \(S\) tendrá \(2^n\) elementos. Esto se debe a que, para cada elemento del conjunto original, hay dos opciones en cada subconjunto posible: el elemento puede estar presente o no. Por lo tanto, con \(n\) elementos, hay \(2^n\) combinaciones posibles.
-
Incluye el Conjunto Vacío y el Conjunto Completo: El conjunto potencia siempre incluirá, como mínimo, el conjunto vacío \(\{∅\}\) y el conjunto completo \(A\) como subconjuntos.
Ejemplo:
A = {1, 2, 3, 4}
P(A) = {∅,{1},{2},{3},{4},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1,2,3},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4}}
Este conjunto potencia tiene \(2^4 = 16\) subconjuntos, como esperaríamos dado que el conjunto original tiene 4 elementos.
Universal Sets
En teoría de conjuntos, un conjunto universal es un conjunto que contiene todos los objetos o elementos bajo consideración para un problema o discusión específica. Es el conjunto que incluye todos los posibles elementos que pueden pertenecer a otros conjuntos definidos en ese contexto. La noción de un conjunto universal es importante porque permite definir complementos de conjuntos y realizar operaciones de conjuntos en un marco completo y cerrado.
Características del Conjunto Universal
- Notación: El conjunto universal a menudo se denota por la letra \(U\) o \(Ω\).
- Complemento: El complemento de un conjunto \(A\) (denotado como \(A^c\) o \(\bar{A}\) dentro de un conjunto universal \(U\) se define como todos los elementos de \(U\) que no están en \(A\).
- Operaciones: Todas las operaciones de conjuntos (unión, intersección, diferencia) se realizan con respecto al conjunto universal si no se especifica otro contexto.
- Depende del Contexto: Lo que constituye el conjunto universal depende del contexto o del dominio del problema. Por ejemplo, en un estudio sobre números enteros, el conjunto de todos los números enteros podría actuar como el conjunto universal. En una discusión sobre colores, el conjunto de todos los colores posibles podría ser el conjunto universal.
Ejemplo
Si estamos trabajando en problemas que involucran los días de la semana, nuestro conjunto universal U podría ser:
U = {Lunes, Martes, Miércoles, Jueves, Viernes, Sábado, Domingo}
Cualquier conjunto de días, como los días laborables o el fin de semana, sería un subconjunto de este conjunto universal.
Operaciones con conjuntos
Python proporciona una amplia gama de operaciones y métodos para trabajar con conjuntos (set y frozenset). Estas operaciones incluyen métodos matemáticos de teoría de conjuntos, así como métodos para añadir y remover elementos. Aquí te detallo la mayoría de ellos:
Métodos para Modificar Conjuntos
.add(elem): Añade un elemento al conjunto..remove(elem): Elimina un elemento del conjunto. Lanza unKeyErrorsi el elemento no existe..discard(elem): Elimina un elemento del conjunto si está presente..pop(): Elimina y retorna un elemento arbitrario del conjunto. Lanza unKeyErrorsi el conjunto está vacío..clear(): Elimina todos los elementos del conjunto.
Métodos para Operaciones de Conjuntos
.union(*others): Retorna un nuevo conjunto con elementos del conjunto y todos los demás (|)..update(*others): Actualiza el conjunto, añadiendo elementos de todos los demás conjuntos (|=)..intersection(*others): Retorna un nuevo conjunto con elementos comunes entre el conjunto y todos los demás (&)..intersection_update(*others): Actualiza el conjunto con la intersección de sí mismo y otros conjuntos (&=)..difference(*others): Retorna un nuevo conjunto con elementos en el conjunto que no están en los otros (-)..difference_update(*others): Actualiza el conjunto, removiendo elementos encontrados en otros conjuntos (-=)..symmetric_difference(other): Retorna un nuevo conjunto con elementos en cualquiera de los conjuntos, pero no en ambos (^)..symmetric_difference_update(other): Actualiza el conjunto con la diferencia simétrica de sí mismo y otro conjunto (^=).
Métodos para Consultas de Conjuntos
.issubset(other): RetornaTruesi todos los elementos del conjunto están en el otro conjunto..issuperset(other): RetornaTruesi el conjunto contiene todos los elementos del otro conjunto..isdisjoint(other): RetornaTruesi dos conjuntos tienen una intersección nula.
Métodos Específicos de frozenset
Los objetos frozenset son inmutables, lo que significa que, una vez creados, no se pueden modificar. Por lo tanto, frozenset no tiene métodos para añadir o remover elementos. Sin embargo, sí soportan operaciones de conjuntos que no modifican el conjunto (como .union, .intersection, etc.), y se pueden usar en contextos donde se necesitan objetos de tipo conjunto que no cambien.
Operadores Equivalentes
Muchas de las operaciones de conjuntos tienen operadores equivalentes:
- Unión:
A | B - Intersección:
A & B - Diferencia:
A - B - Diferencia simétrica:
A ^ B
Ejemplo Básico de Uso
A = {1, 2, 3}
B = {3, 4, 5}
# Unión
print(A | B) # {1, 2, 3, 4, 5}
# Intersección
print(A & B) # {3}
# Diferencia
print(A - B) # {1, 2}
# Diferencia simétrica
print(A ^ B) # {1, 2, 4, 5}
Estos métodos y operaciones hacen de los conjuntos en Python una herramienta poderosa y flexible para el manejo de colecciones únicas de elementos y la implementación de lógica de teoría de conjuntos.
Leyes de Morgan
Las leyes de De Morgan son principios fundamentales en la lógica y la teoría de conjuntos que describen cómo interactúan las operaciones de complemento con las operaciones de unión e intersección de conjuntos. Nombradas en honor al matemático y lógico británico Augustus De Morgan, estas leyes tienen aplicaciones significativas en varias áreas, incluida la lógica proposicional, el diseño de circuitos digitales, la teoría de la probabilidad, y más.
Las leyes de De Morgan establecen que:
Primera Ley de De Morgan
El complemento de la unión de dos conjuntos es igual a la intersección de sus complementos. Esto se puede escribir como: \((A∪B)^c = A^c ∩ B^c\)
Esto significa que si tomas dos conjuntos \(A\) y \(B\), y buscas el conjunto de todos los elementos que no están ni en \(A\) ni en \(B\), obtendrás el mismo resultado que si primero encontraras los elementos que no están en \(A\), los elementos que no están en \(B\), y luego tomaras todos los elementos que son comunes a estos dos subconjuntos.
# cojunto universal U, del cual A y B son subconjuntos
U = {1, 2, 3, 4, 5, 6}
A = {1, 2, 3}
B = {3, 4, 5}
union_complement = U - (A.union(B)) # {6}
complement_intersection = (U - A).intersection(U - B) # {6}
assert union_complement == complement_intersection # true
Segunda Ley de De Morgan
El complemento de la intersección de dos conjuntos es igual a la unión de sus complementos. Se puede escribir como: \((A∩B)^c = A^c ∪ B^c\)
Esto significa que si tomas dos conjuntos \(A\) y \(B\), y buscas el conjunto de todos los elementos que no están tanto en \(A\) como en \(B\) al mismo tiempo, obtendrás el mismo resultado que si primero encontraras los elementos que no están en \(A\) y los elementos que no están en \(B\), y luego tomaras la unión de estos dos subconjuntos.
# cojunto universal U, del cual A y B son subconjuntos
U = {1, 2, 3, 4, 5, 6}
A = {1, 2, 3}
B = {3, 4, 5}
intersection_complement = U - (A.intersection(B)) # (A ∩ B)'
complement_union = (U - A).union(U - B) # A' U B'
assert intersection_complement == complement_union
Los resultados de las operaciones según las leyes de De Morgan deberían ser iguales, lo cual es verificado por los assert, asegurando que ambos lados de las leyes sean equivalentes en cada caso.
Importancia de las Leyes de De Morgan
Las leyes de De Morgan son herramientas poderosas para simplificar expresiones lógicas y operaciones de conjunto. Son especialmente útiles en las siguientes situaciones:
- Simplificación de Expresiones Booleanas: En electrónica y ciencias de la computación, las leyes de De Morgan se utilizan para simplificar y minimizar las expresiones booleanas en el diseño de circuitos lógicos.
- Manipulación de Conjuntos en Matemáticas: Ayudan a realizar operaciones de conjunto de manera más eficiente, especialmente cuando se trata de complementos.
- Demostraciones en Teoría de Conjuntos: Son fundamentales en la demostración de propiedades y teoremas relacionados con conjuntos.
- Filtrado de Datos: En programación, estas leyes pueden ser útiles para optimizar consultas y operaciones que involucran filtrado de datos basado en múltiples condiciones.
Venn Diagrams Operations
Los diagramas de Venn como una herramienta útil para representar visualmente operaciones y relaciones entre conjuntos, incluyendo la unión, intersección, diferencia, complementos, así como las relaciones de subconjuntos, superconjuntos y particiones.
Los diagramas de Venn utilizan figuras que típicamente se sitúan dentro de un rectángulo o un espacio que simboliza el conjunto universal, dentro del cual los círculos o formas representan conjuntos individuales.
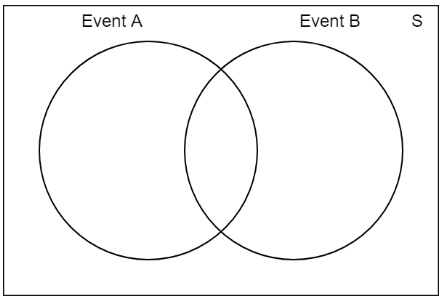
Unión
La unión de dos conjuntos engloba cualquier elemento que exista en uno o en ambos. Podemos representar esto visualmente como un diagrama de Venn .
Por ejemplo, digamos que tenemos dos conjuntos, \(A\) y \(B\).
- A representa lanzar un número impar con un dado de seis caras: \(A = \{1, 3, 5\}\).
- B representa sacar un número mayor que dos: \(B = \{3, 4, 5, 6\}\).
La unión de estos dos conjuntos sería todo en el conjunto \(A\) , el conjunto \(B\) o ambos: \(\{1, 3, 4, 5, 6\}\). Podemos escribir la unión de dos eventos matemáticamente como \(A ∪ B\).
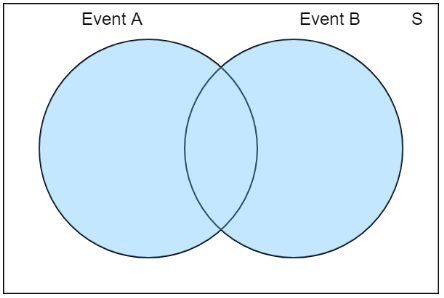
Intersección
La intersección de dos conjuntos abarca cualquier elemento que exista en ambos conjuntos. Visualmente:
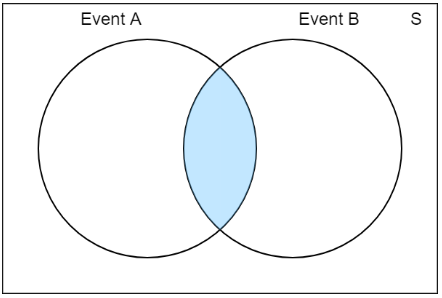
La intersección de los conjuntos anteriores (\(A\) representa sacar un número impar en un dado de seis caras y \(B\) representa sacar un número mayor que dos) incluye cualquier valor que aparezca en ambos conjuntos: \(\{3, 5\}\) . Podemos escribir matemáticamente la intersección de dos eventos como \(P(A ∩ B)\).
Complemento
Por último, el complemento de un conjunto consta de todos los resultados posibles fuera del conjunto. Visualmente:
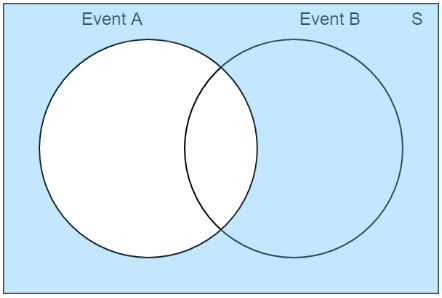
Considere el conjunto \(A\) del ejemplo anterior (lanzando un número impar en un dado de 6 caras). El complemento de este conjunto sería sacar un número par: \(\{2, 4, 6\}\) . Podemos escribir el complemento del conjunto \(A\) como \(AC\) . Una característica clave de los complementos es que un conjunto y su complemento cubren todo el espacio muestral. En este ejemplo de tirada de dado, el conjunto de números pares e impares cubriría todas las tiradas posibles: \(\{1, 2, 3, 4, 5, 6\}\) .
Ejemplo 1:
Interseccion y union de dos eventos:
A = {1, 2, 3}
B = {1, 2, 3, 4, 6}
Interseccion:
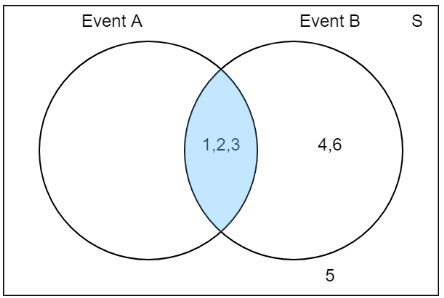
Union:
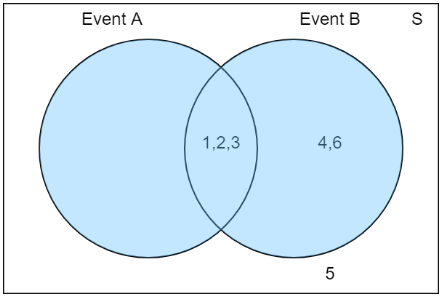
Complemento de A:
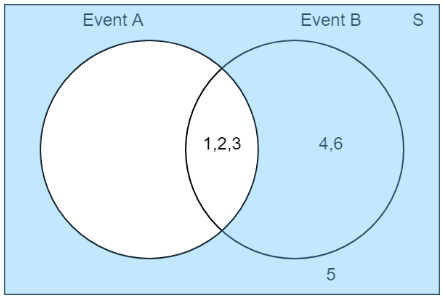
Complemento de B:
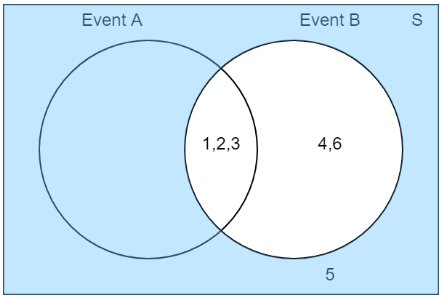
Ejemplo 2:
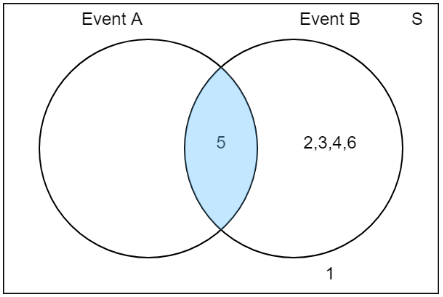
Interseccion y union de dos eventos:
A = {5}
B = {2, 3, 4, 5, 6}
Interseccion:
En el siguinete enlace hay un programa interactivo que muestra la union y la interseccion de dos eventos segun el resultado de lanzar dados: