Correlacion entre variables cuantitativas y categoricas

Examinar la relación entre variables puede brindarnos información clave sobre nuestros datos. En esta lección, cubriremos formas de evaluar la asociación entre una variable cuantitativa y una variable categórica.

En los próximos ejercicios, exploraremos un conjunto de datos que contiene la siguiente información sobre estudiantes de dos escuelas portuguesas:

• school: la escuela a la que asiste cada alumno, Gabriel Periera ( ‘GP’) o Mousinho da Silveria ( ‘MS’)
• address: la ubicación de la casa del estudiante ( ‘U’ para zonas urbanas y ‘R’ rurales) absences: el número de veces que el estudiante estuvo ausente durante el año escolar
• Mjob: la industria laboral de la madre del estudiante
• Fjob: la industria laboral del padre del estudiante
• G3: la puntuación del estudiante en una evaluación de matemáticas, que va de 0 a 20

Supongamos que queremos saber: ¿La puntuación de un estudiante (G3) está asociada con su escuela (school)? Si es así, saber a qué escuela asiste un estudiante nos da información sobre cuál será su puntuación probable. Por ejemplo, tal vez los estudiantes de una de las escuelas obtengan consistentemente calificaciones más altas que los estudiantes de la otra escuela.

Para empezar a responder esta pregunta, resulta útil guardar las puntuaciones de cada escuela en dos listas separadas:

scores_GP = students.G3[students.school == 'GP']
scores_MS = students.G3[students.school == 'MS']

Diferencias de medias y medianas

Para investigar si existe o no una asociación entre los puntajes de matemáticas y la escuela a la que asiste el estudiante. Podemos comenzar a cuantificar esta asociación utilizando dos estadísticas resumidas comunes: diferencias de medias y medianas. Para calcular la diferencia en las puntuaciones medias de G3 de las dos escuelas, podemos comenzar encontrando la puntuación media en matemáticas de los estudiantes de cada escuela. Luego podemos encontrar la diferencia entre ellos:

mean_GP = np.mean(scores_GP)
mean_MS = np.mean(scores_MS)
print(mean_GP) #output: 10.49
print(mean_MS) #output: 9.85
print(mean_GP - mean_MS) #Output: 0.64

Para calcular la diferencia de medianas se utilizaria el mismo procedimiento.

# Calcular la media de los puntajes de matematicas de cada escuela
scores_urban_mean = np.mean(scores_urban)
scores_rural_mean = np.mean(scores_rural)
# Calcular las diferencias
mean_diff = scores_urban_mean - scores_rural_mean

print(f'Media de los puntajes de Matematicas, escuela urbana: {scores_urban_mean:.2f}')
print(f'Media de los puntajes de Matematicas, escuela rural: {scores_rural_mean:.2f}')
print(f'Diferencia de las medias de las escuelas: {mean_diff:.2f} ')


# Calcular la mediana de los puntajes de matematica de cada escuela
scores_urban_median = np.median(scores_urban)
scores_rural_median = np.median(scores_rural)
# Calcular las diferencias
median_diff = scores_urban_median - scores_rural_median

print(f'Mediana de los puntajes de Matematicas, escuela urbana: {scores_urban_median:.2f}')
print(f'Mediana de los puntajes de Matematicas, escuela rural: {scores_rural_median:.2f}')
print(f'Diferencia de las medianas de las escuelas: {median_diff:.2f} ')

Output

Media de los puntajes de Matematicas, escuela urbana: 11.62
Media de los puntajes de Matematicas, escuela rural: 10.60
Diferencia de las medias de las escuelas: 1.02 
Mediana de los puntajes de Matematicas, escuela urbana: 12.00
Mediana de los puntajes de Matematicas, escuela rural: 11.00
Diferencia de las medianas de las escuelas: 1.00 

Diagramas de caja uno al lado del otro

La diferencia en las puntuaciones medias de matemáticas de los estudiantes fue de 1.02. ¿Cómo sabemos si esta diferencia se considera pequeña o grande? Para responder a esta pregunta, necesitamos saber algo sobre la difusión de los datos.

Una forma de tener una mejor idea de la propagación es observar una representación visual de los datos. Los diagramas de caja uno al lado del otro son útiles para visualizar las diferencias de medias y medianas porque nos permiten estimar visualmente la variación de los datos. Esto puede ayudarnos a determinar si las diferencias de medias o medianas son “grandes” o “pequeñas”. Echemos un vistazo a los diagramas de caja de los puntajes de matemáticas en cada escuela:

sns.boxplot(data = students, x = 'address', y = 'G3')
plt.show()

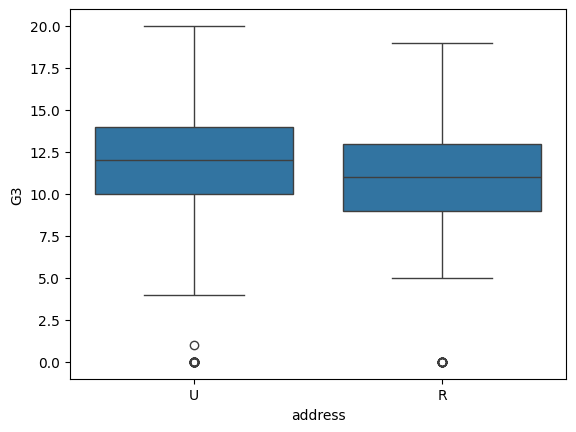
Inspeccionar histogramas superpuestos

Otra forma de explorar la relación entre una variable cuantitativa y categórica con más detalle es inspeccionando histogramas superpuestos. En el código siguiente, la configuración alpha = 0.5 garantiza que los histogramas sean lo suficientemente transparentes como para que podamos verlos a ambos a la vez. También se utiliza density=True asegurado de que el eje y sea una densidad en lugar de una frecuencia.

plt.hist(scores_urban , color="blue", label="Urban", density=True, alpha=0.5)
plt.hist(scores_rural , color="red", label="Rural", density=True, alpha=0.5)
plt.legend()
plt.show()

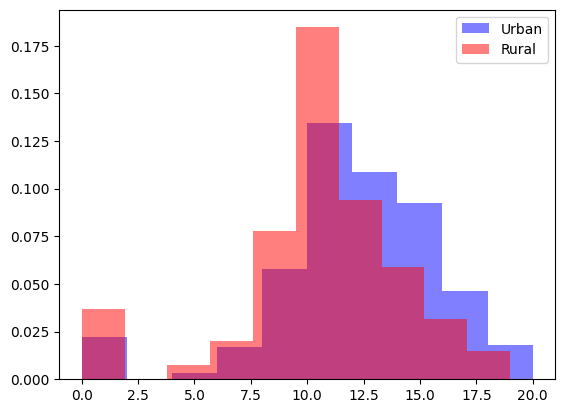
Al inspeccionar este histograma, podemos ver claramente que toda la distribución de las puntuaciones en Urban (no solo la media o la mediana) aparece ligeramente desplazada hacia la derecha (más arriba) en comparación con las puntuaciones en Rural. Sin embargo, todavía hay mucha superposición entre las puntuaciones, lo que sugiere que la asociación es relativamente débil.

Tenga en cuenta que solo hay 46 estudiantes en MS, pero hay 349 estudiantes en GP. Si no hubiéramos usado density=True, nuestro histograma se habría visto así, haciendo imposible comparar las distribuciones de manera justa.

Si bien los histogramas superpuestos y los diagramas de caja uno al lado del otro pueden transmitir información similar, los histogramas nos brindan más detalles y pueden ser útiles para detectar patrones que no eran visibles en un diagrama de caja (por ejemplo, una distribución bimodal).

Explorando variables categóricas no binarias

En cada uno de los ejercicios anteriores, evaluamos si existía una asociación entre una variable cuantitativa (puntuaciones de matemáticas) y una variable categórica BINARIA (escuela). La variable categórica se considera binaria porque sólo hay dos opciones disponibles, Urban o Rural. Sin embargo, a veces nos interesa una asociación entre una variable cuantitativa y una variable categórica no binaria. Las variables categóricas no binarias tienen más de dos categorías.

Al observar una asociación entre una variable cuantitativa y una variable categórica no binaria, debemos examinar todas las diferencias por pares. Por ejemplo, supongamos que queremos saber si existe o no una asociación entre las puntuaciones de matemáticas G3 y Mjob, una variable categórica que representa el trabajo de la madre. Esta variable tiene cinco categorías posibles:

• at_home
• health
• services
• teacher
• other

En realidad, hay 10 comparaciones diferentes que podemos hacer. Por ejemplo, podemos comparar puntuaciones de estudiantes cuyas madres trabajan at_home o en health; at_home o other; etc. La forma más sencilla de visualizar rápidamente estas comparaciones es con diagramas de caja uno al lado del otro:

sns.boxplot(data = students, x = 'Mjob', y = 'G3')
plt.show()

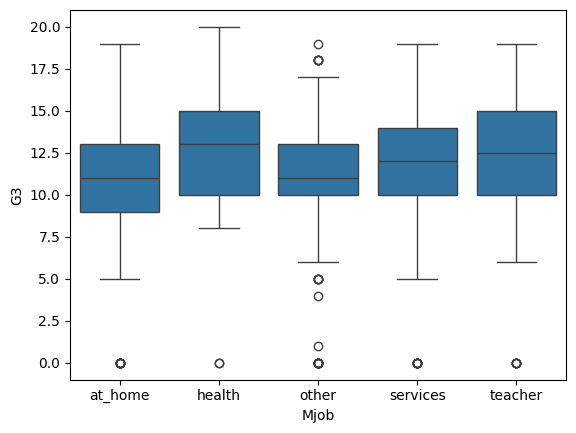
Visualmente, necesitamos comparar cada cuadro con todos los demás. Si bien la mayoría de estos cuadros se superponen entre sí, hay algunos pares en los que existen algunas diferencias aparentes. Por ejemplo, las puntuaciones parecen ser más altas entre los estudiantes cuyas madres trabajan en el sector de la salud que entre los estudiantes cuyas madres trabajan en casa o en “otro” trabajo. Si hay CUALQUIER diferencia por pares, podemos decir que las variables están asociadas; sin embargo, es más útil informar específicamente qué grupos son diferentes.