Contenido
- Variables aleatorias continuas
- Zero Probability to Individual Values
- Probability Density Functions
- Continuos Uniform Distribution
- Exponential Random Variables
- Gaussian Random Variables (Normal Random Variables)
- [Función de Distribución Acumulativa con variables continuas]
- Transformacion de Variables Aleatorias
Modelos de probabilidad hacia variables aleatoria
Las variables aleatorias son entidades matemáticas que asignan resultados de procesos aleatorios a valores numéricos. Son fundamentales para describir fenómenos en términos cuantitativos, permitiendo el uso de herramientas matemáticas y estadísticas para análisis y predicción. Estas variables nos permiten la transición de conceptos teóricos de probabilidad a su aplicación práctica para modelar y analizar datos reales.
Este paso es crucial, ya que en el aprendizaje automático, los datos —y, por ende, los eventos que representan— se expresan casi exclusivamente a través de números. Aquí, se propone una sólida comprensión de cómo los principios de probabilidad y estadística subyacen en la base de modelos complejos de aprendizaje automático, particularmente a través del ejemplo del reconocimiento facial.
Modelos de probabilidad continua
En los modelos de probabilidad discretos donde el espacio muestral es contable. Esto significa que, ya sea finito o infinito, los resultados posibles de nuestro experimento se pueden enumerar o indexar de manera secuencial. Estos odelos permiten asignar probabilidades positivas a eventos específicos, incluso a aquellos que contienen un único resultado.
Sin embargo, nos encontramos con una complejidad adicional cuando el espacio muestral se vuelve incontable. Imaginemos, por ejemplo, una rueda de dardos. Si consideramos el punto donde impacta el dardo dentro de un círculo unitario, cada punto tiene la misma probabilidad de ser elegido. Pero, ¿cómo asignamos probabilidades a eventos tan infinitesimales como un punto específico dentro del círculo?
Cuando el espacio muestral es incontable, asignar probabilidades positivas a cada evento individual resulta imposible. Incluso asignando la más mínima probabilidad positiva a cada posible punto de impacto del dardo en el círculo, nos encontraríamos rápidamente con que la suma total de estas probabilidades excedería el límite de 1, violando así los axiomas fundamentales de la probabilidad.
La Solución: Trabajar con Intervalos
En los modelos de probabilidad continua, en lugar de tratar con eventos individuales, trabajamos con intervalos de eventos. No asignamos probabilidades a puntos específicos, sino a la probabilidad de que un evento ocurra dentro de un rango determinado. Por ejemplo, en lugar de preguntar por la probabilidad de que el dardo impacte exactamente a una distancia de 0.73 del centro, preguntaríamos por la probabilidad de que impacte dentro de un intervalo, como entre 0.5 y 0.7.
Consideremos un círculo unitario. Si el juego consiste en lanzar un dardo y calcular la distancia desde el origen hasta el punto de impacto, nos enfrentamos a un espacio muestral incontable. Cada punto dentro del círculo tiene una probabilidad de ser alcanzado, pero es imposible asignar una probabilidad específica a cada punto. En cambio, debemos enfocarnos en los intervalos de distancia.
Espacio Muestral y Probabilidades en Modelos Discretos y Continuos
Antes de adentrarnos en ejemplos, es importante recordar la diferencia entre modelos de probabilidad discretos y continuos:
Modelos Discretos: El espacio muestral es contable, lo que significa que podemos enumerar todos los posibles resultados del experimento.
Modelos Continuos: El espacio muestral es incontable, como los puntos en un segmento de línea. Aquí, no podemos asignar probabilidades a eventos individuales de manera directa.
Variables aleatorias continuas
Cuando los valores posibles de una variable aleatoria son incontables, se le llama variable aleatoria continua. Generalmente son variables de medición y no se pueden contar porque las mediciones siempre pueden ser más precisas: metros, centímetros, milímetros, etc.
Por ejemplo, la temperatura en Los Ángeles en un día elegido al azar es una variable aleatoria continua. Siempre podemos ser más precisos sobre la temperatura expandiendo a otro decimal (96 grados, 96,44 grados, 96,437 grados, etc.).
Zero Probability to Individual Values
¿Podemos realmente decir que es imposible que ocurran eventos de probabilidad cero? No se puede encontrar ningún ejemplo mientras se permanece en el ámbito de los espacios muestrales finitos. Por otro lado, en espacios muestrales infinitos , abundan los posibles resultados de probabilidad cero. Las variables aleatorias continuas pueden tomar cualquier valor dentro de un intervalo continuo, y estos valores son no numerables.
Experimento del Círculo Unitario
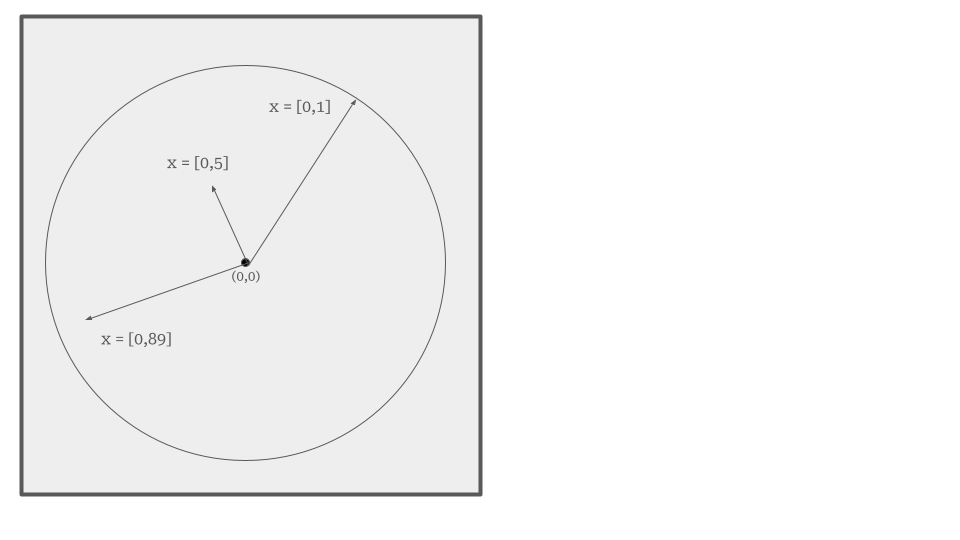
Consideremos un experimento ilustrativo para entender mejor las variables aleatorias continuas. Imaginemos un círculo unitario, es decir, un círculo de radio uno, centrado en el origen de un sistema de coordenadas. En este experimento, el acto aleatorio consiste en colocar puntos dentro del círculo. La variable de interés en este caso es la distancia desde el origen hasta el punto donde cada punto es colocado aleatoriamente.
En este experimento, la variable aleatoria que define la distancia desde el origen hasta el punto puede tomar cualquier valor entre 0 y 1. El valor 0 se alcanzaría si el punto cae exactamente en el centro del círculo (el origen), mientras que el valor 1 se alcanza si el punto cae en cualquier parte del perímetro del círculo. Entre estos dos extremos, hay infinitos valores posibles que la distancia podría tomar, como 0.1, 0.001, 0.7213, etc. Estos valores forman un continuo y son ejemplos de una variable aleatoria continua.
Si consideramos anillos concéntricos dentro del círculo, cada anillo podría representar un intervalo específico para \(X\), y la probabilidad de que \(X\) tome un valor dentro de un anillo sería proporcional al área de ese anillo.
Asignación de Probabilidades
En el caso de variables continuas, la asignación de probabilidades presenta desafíos únicos. En teoría, la probabilidad de que la variable aleatoria tome un valor específico exacto dentro del intervalo es cero. Esto se debe a que la cantidad de posibles valores en un intervalo continuo es infinita, y asignar una probabilidad positiva a cada posible valor individual resultaría en una suma de probabilidades que excedería 1, violando la propiedad de normalización de probabilidades.
Para manejar probabilidades en el caso de variables continuas, utilizamos lo que se conoce comoFunciones de Densidad de Probabilidad (PDF) . Estas funciones no asignan probabilidades a valores individuales sino que describen la densidad de probabilidad en diferentes regiones del espacio de valores de la variable.
Por ejemplo, en lugar de preguntar cuál es la probabilidad de que la variable aleatoria sea exactamente 0.5, utilizamos la PDF para determinar la probabilidad de que la variable esté dentro de un intervalo, como entre 0.3 y 0.7.
Probability Density Functions
En el estudio de las variables aleatorias continuas, las Funciones de Densidad de Probabilidad (PDFs, por sus siglas en inglés) son esenciales para modelar y comprender la distribución de probabilidad de estas variables. A diferencia de las Funciones de Masa de Probabilidad (PMFs), que asignan probabilidades a valores específicos de variables discretas, las PDFs se utilizan para construir modelos de probabilidad sobre intervalos de variables continuas.
Conceptos Básicos de PDFs
Una Funcion de Densidad de Probabilidad de no proporciona directamente la probabilidad de un valor específico; en cambio, describe cómo se distribuye la probabilidad a lo largo de un intervalo de posibles valores. En el contexto de las variables continuas, una PDF es útil para calcular la probabilidad de que la variable caiga dentro de un rango específico.
Modelado de Probabilidades:
- Para construir una PDF, se puede comenzar definiendo la función en todo su rango posible, asegurando que el área bajo la curva de la función sea igual a uno.
- Por ejemplo, para una variable \(X\) uniforme que varía de 0 a 1, una PDF simple podría ser una función constante donde el valor de la función (altura) es siempre 1 en el intervalo [0,1].
Cálculo de Probabilidades:
- Para calcular la probabilidad de que \(X\) esté en un intervalo específico, como entre 0.2 y 0.4, calculamos el área bajo la PDF en ese intervalo.
- Esta área se obtiene integrando la función de densidad de probabilidad desde 0.2 hasta 0.4, y el resultado representa la probabilidad de que \(X\) caiga dentro de ese rango.
Propiedades Clave de las PDFs
-
Positividad: Todos los valores de una PDF deben ser no negativos, una propiedad compartida con las PMFs.
-
Integración a Uno: A diferencia de las PMFs, donde cada valor individual puede tener una probabilidad directamente asignada (y sumar todas las probabilidades da uno), en las PDFs el total del área bajo la curva debe ser igual a uno para que el modelo de probabilidad sea válido.
-
Diferencias con PMFs: Mientras que los valores de una PMF siempre deben ser menores o iguales a uno, los valores de una PDF pueden ser mayores que uno, siempre que el área bajo la curva se mantenga en uno. Esto es importante porque los valores de la PDF no representan probabilidades directas sino densidades de probabilidad, que ayudan a calcular probabilidades sobre intervalos.
Continuos Uniform Distribution
La distribución uniforme continua es un modelo estadístico esencial que se utiliza para describir situaciones donde todos los eventos en un intervalo específico son igualmente probables. Esta distribución es particularmente útil para simular y modelar fenómenos en los cuales no hay preferencia por ningún valor dentro del rango establecido.
Una variable aleatoria \(X\) se dice que sigue una distribución uniforme continua sobre un intervalo \([a, b]\) si cada valor dentro de este intervalo es igualmente probable. Esto implica que la función de densidad de probabilidad (PDF) para \(X\) es constante dentro de \([a, b]\) y cero fuera de este rango.
Para una variable aleatoria \(X\) que es uniforme sobre el intervalo \([10, 30]\)
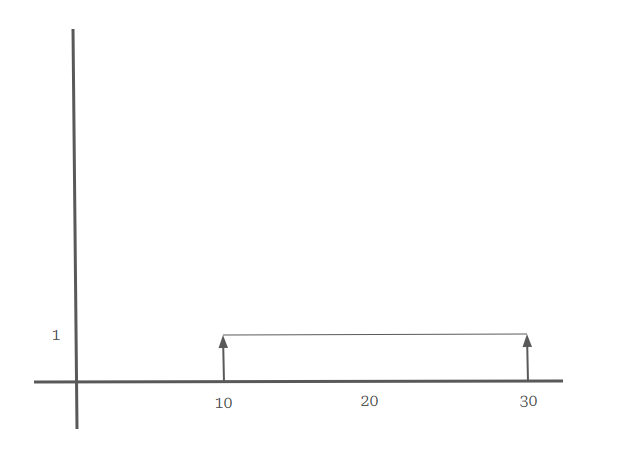
Esta forma de la función garantiza que la probabilidad de cualquier subintervalo dentro de \([10, 30]\) sea proporcional a su longitud. La constante \(\frac{1}{20}\) se deriva de la inversa de la longitud del intervalo \((30 - 10 = 20)\), asegurando que el área total bajo la curva de la PDF sea 1, cumpliendo así con una propiedad fundamental de las distribuciones de probabilidad.
Ejemplo Práctico de la Distribución Uniforme
Supongamos que queremos calcular la probabilidad de que \(X\) caiga entre 15 y 20. Dado que la altura de la función de densidad es \(\frac{1}{20}\) en todo el intervalo \([10, 30]\), el cálculo de esta probabilidad se reduce a evaluar el área de un rectángulo definido por el intervalo \([15, 20]\):
\[P(15 \leq X \leq 20) = \frac{1}{20} \times (20 - 15) = \frac{1}{20} \times 5 = \frac{1}{4}\]Esto indica que hay una probabilidad del 25% de que \(X\) esté entre 15 y 20.
Aplicación en Simulaciones
La distribución uniforme es ampliamente utilizada en la generación de números aleatorios, especialmente en simulaciones computacionales. Por ejemplo, la función np.random.rand() en Python genera números aleatorios uniformemente distribuidos en el intervalo \([0, 1]\). Estos valores pueden ser escalados a cualquier otro intervalo \([a, b]\) mediante la transformación:
Esto es particularmente útil en estudios de simulación donde se requieren entradas aleatorias que sean equitativas en términos de probabilidad a lo largo de un intervalo dado.
Implementar Uniform Distributions con Python
import matplotlib.pyplot as plt
import seaborn as sns
X = 100 * np.random.rand(100000)+20
plt.hist(X, density=True, bins=50)
sns.kdeplot(X)
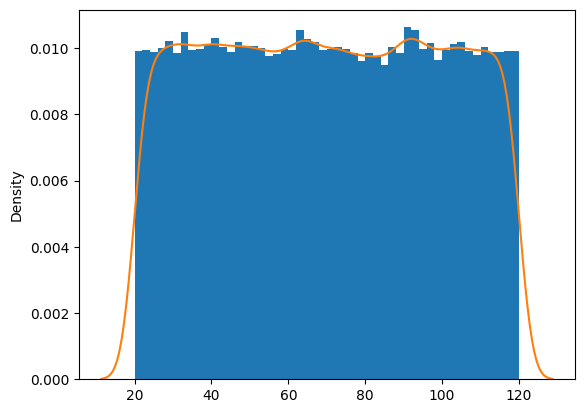
Exponential Random Variables
Las variables aleatorias exponenciales son un tipo importante de distribución de probabilidad continua que se utiliza para modelar el tiempo entre eventos en procesos que son continuos y sin memoria. Esta distribución es especialmente útil en el ámbito de la teoría de colas, la fiabilidad de sistemas y en la modelación de procesos de llegada en sistemas de comunicaciones.
Una variable aleatoria exponencial, denotada como \(X\), describe el tiempo entre eventos en un proceso de Poisson, donde los eventos ocurren de manera continua e independiente a una tasa constante. Matemáticamente, la función de densidad de probabilidad (PDF) de una variable aleatoria exponencial está dada por:
\[f(x; \lambda) = \lambda e^{-\lambda x} \quad \text{para } x \geq 0\]Donde:
- \(\lambda\) es la tasa de llegada o tasa de fallo, también conocida como parámetro de tasa, que indica el número promedio de eventos por unidad de tiempo.
- \(e\) es la base del logaritmo natural.
- \(x\) representa el tiempo.
Las principales características de esta distribución incluyen:
- Sin memoria: La distribución exponencial es la única distribución continua que tiene la propiedad de falta de memoria, lo que significa que la probabilidad de que ocurra un evento en el futuro es independiente de cualquier historia pasada.
- Media y Varianza:
- La media (esperanza) de \(X\) es \(\frac{1}{\lambda}\).
- La varianza de \(X\) es \(\frac{1}{\lambda^2}\).
Ejemplos de Aplicación
-
Teoría de Colas: En el análisis de colas, la distribución exponencial se utiliza para modelar los tiempos de llegada de clientes a un servicio o los tiempos de servicio necesarios en puntos de atención.
-
Fiabilidad de Sistemas: En ingeniería de fiabilidad, se utiliza para modelar el tiempo hasta el fallo de componentes electrónicos o mecánicos. Por ejemplo, si un componente tiene una tasa de fallo constante de ( \lambda ) fallos por hora, el tiempo hasta el fallo del componente puede modelarse como una variable aleatoria exponencial.
-
Procesos de Llegada en Redes de Comunicación: En telecomunicaciones, los tiempos entre llegadas de paquetes de datos pueden modelarse utilizando distribuciones exponenciales.
Simulación en Python
Aquí se presenta un ejemplo básico de cómo generar y visualizar variables aleatorias exponenciales utilizando Python y NumPy:
import numpy as np
import matplotlib.pyplot as plt
# Parámetro de tasa
lambda_param = 1.0
# Generar 1000 variables aleatorias exponenciales
data = np.random.exponential(1/lambda_param, 1000)
# Visualizar los datos
plt.hist(data, bins=50, density=True, alpha=0.75, label='Datos simulados')
plt.title('Histograma de Variables Aleatorias Exponenciales')
plt.xlabel('Tiempo')
plt.ylabel('Densidad')
plt.legend()
plt.show()
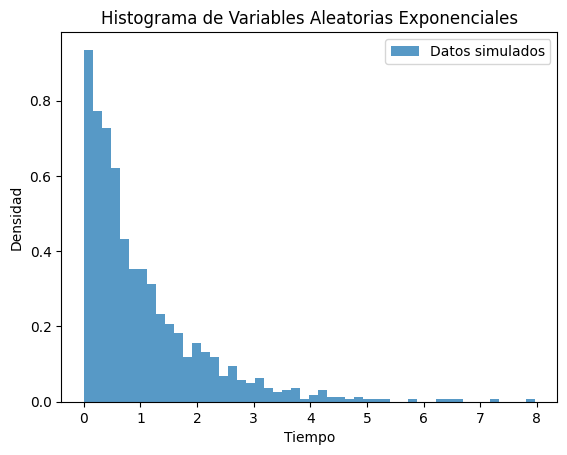
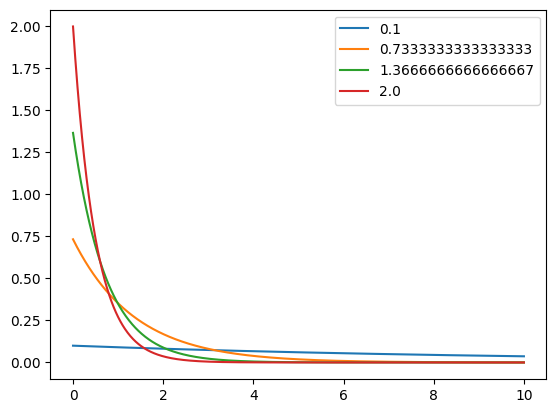
El código siguiente utiliza NumPy y Matplotlib para visualizar la función de densidad de probabilidad (PDF) de varias distribuciones exponenciales con diferentes parámetros de tasa.
# Importar las bibliotecas necesarias para el manejo de arrays y visualización
import numpy as np
import matplotlib.pyplot as plt
# Generar 1000 puntos equidistantes en el rango de 0 a 10
x = np.linspace(0, 10, 1000)
# Crear diferentes valores del parámetro de tasa 'lambda', desde 0.1 hasta 2, en total 4 valores
lmdaz = np.linspace(0.1, 2, 4)
# Iterar sobre cada valor de lambda
for i in lmdaz:
# Calcular la función de densidad de probabilidad exponencial para cada valor de x y lambda
fx = i * np.exp(-i * x) # f(x) = lambda * exp(-lambda * x)
# Graficar la función calculada, etiquetando con el valor de lambda correspondiente
plt.plot(x, fx, label=str(i))
# Añadir una leyenda al gráfico, que muestra las etiquetas de los valores de lambda
plt.legend()
# Mostrar el gráfico resultante
plt.show()
Gaussian Random Variables (Normal Random Variables)
La variable aleatoria gaussiana, también conocida como variable aleatoria normal, es fundamental tanto en los ámbitos teóricos como prácticos del aprendizaje automático. Su importancia surge de su capacidad para modelar numerosos fenómenos naturales y su extenso uso en algoritmos.
Una variable aleatoria gaussiana \(X\) se define por su capacidad para tomar cualquier valor real, efectivamente abarcando desde \(-\infty\) hasta \(+\infty\). Esta característica subraya su versatilidad en la modelización estadística, donde puede representar una amplia gama de distribuciones de datos.
La función de densidad de probabilidad (PDF) de una variable aleatoria gaussiana es uno de sus aspectos más cruciales. Se expresa matemáticamente como:
\[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)\]Aquí, \(\mu\) representa la media, o el centro de la distribución, mientras que \(\sigma^2\) denota la varianza, dictando la dispersión de los datos alrededor de la media. La forma de la función es simétricamente campaniforme, alcanzando su máximo en \(\mu\) y decayendo a medida que los valores se alejan de la media, lo que indica que la probabilidad de observar valores cercanos a \(\mu\) es más alta.
Comprensión Conceptual a Través de Funciones Exponenciales
Para comprender el comportamiento de la PDF gaussiana, se puede considerar el papel de la función exponencial en la fórmula. Por ejemplo, usando la base exponencial \(e\) (un número positivo mayor que uno), a medida que \(x\) se desvía de \(\mu\), el término \(e^{-\frac{(x-\mu)^2}{2\sigma^2}}\) disminuye rápidamente. Esto demuestra cómo la densidad de probabilidad disminuye simétricamente a medida que los valores se alejan de la media, enfatizando la naturaleza “normal” de la distribución de datos alrededor de la media.
Ejemplos Prácticos: Simulación y Visualización
Para calcular la Función de Densidad de Probabilidad (PDF) de una distribución Gaussiana (o normal) en Python, puedes utilizar la librería scipy.stats. La distribución Gaussiana se define por dos parámetros principales: la media \(\mu\\) y la desviación estándar \(\sigma\).
Aquí tienes un ejemplo práctico de cómo calcular la PDF gaussiana para un valor específico usando scipy.stats.norm:
from scipy.stats import norm
# Parámetros de la distribución
mu = 0 # Media
sigma = 1 # Desviación estándar
# Crear un objeto de distribución normal
distribucion_normal = norm(loc=mu, scale=sigma)
# Calcular la PDF en un punto específico, por ejemplo x = 1
x = 1
pdf_value = distribucion_normal.pdf(x)
print("La PDF de una distribución normal estándar en x = 1 es:", pdf_value)
Este código configura una distribución normal estándar (con media 0 y desviación estándar 1) y calcula la PDF en el punto \(x = 1\). Puedes cambiar los valores de mu y sigma para ajustar la distribución a tus necesidades, y calcular la PDF en cualquier punto que requieras.
Función para Calcular la PDF de una Distribución Gaussiana
Si prefieres implementar la función manualmente sin usar scipy, aquí tienes un ejemplo de cómo hacerlo:
import math
def gaussian_pdf(x, mu, sigma):
# Factor constante de la PDF gaussiana
const = 1 / (math.sqrt(2 * math.pi * sigma ** 2))
# Exponente de la función exponencial
exponente = -((x - mu) ** 2) / (2 * sigma ** 2)
return const * math.exp(exponente)
# Ejemplo de uso
x = 1
mu = 0
sigma = 1
pdf_value = gaussian_pdf(x, mu, sigma)
print("La PDF de una distribución normal estándar en x = 1 es:", pdf_value)
Este código implementa la misma fórmula de la PDF gaussiana de forma explícita, lo que te permite entender claramente cómo se estructura la función.
Visualización
Para visualizar la función de densidad de probabilidad (PDF) de una distribución gaussiana en Python, puedes usar la biblioteca de visualización matplotlib junto con numpy para generar los puntos de datos y scipy.stats para calcular los valores de la PDF. A continuación, te muestro cómo crear una visualización de la PDF para una distribución normal estándar y otra con diferentes parámetros.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parámetros de la distribución
mu = 0 # Media
sigma = 1 # Desviación estándar
# Generar puntos de datos para el eje x
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 1000)
# Crear un objeto de distribución normal
distribucion_normal = norm(loc=mu, scale=sigma)
# Calcular la PDF para cada punto x
pdf_values = distribucion_normal.pdf(x)
# Crear el gráfico
plt.figure(figsize=(8, 4))
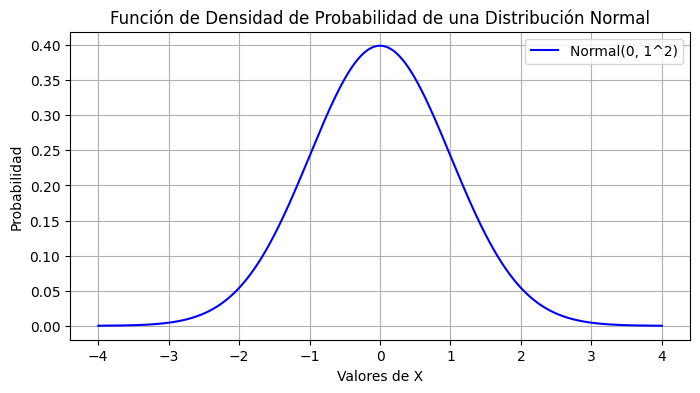
plt.plot(x, pdf_values, label=f'Normal({mu}, {sigma}^2)', color='blue')
plt.title('Función de Densidad de Probabilidad de una Distribución Normal')
plt.xlabel('Valores de X')
plt.ylabel('Probabilidad')
plt.legend()
plt.grid(True)
plt.show()
Explicación del Código
-
Importación de Librerías: Se importan
numpypara operaciones numéricas,matplotlib.pyplotpara la visualización, ynormdescipy.statspara trabajar con la distribución normal. -
Parámetros de la Distribución: Se define la media (
mu) y la desviación estándar (sigma). -
Generación de Puntos: Se utilizan
np.linspacepara crear un arreglo de 1000 puntos en el eje x, que cubre desde \(\mu - 4\sigma\) hasta \(\mu + 4\sigma\). Esto asegura que se incluya la mayoría de la masa de la distribución. -
Cálculo de la PDF: Se utiliza el método
pdfdel objeto de distribución normal para calcular la probabilidad en cada uno de los puntos x generados. -
Creación de la Gráfica: Se usa
matplotlib.pyplotpara crear una gráfica lineal de los valores de x contra los valores de la PDF. Se configura el título, etiquetas de los ejes, leyenda, y se activa la cuadrícula para mejor visualización.
Esta visualización te permite observar claramente cómo es la forma de campana de la distribución gaussiana, y cómo varían las probabilidades con respecto a la distancia de la media. Puedes modificar mu y sigma en el código para ver cómo cambia la forma de la distribución con diferentes parámetros.
Función de Distribución Acumulativa en variables continuas y Mixtas
Función de Distribución Acumulativa (CDF) para Variables Continuas
Se define como la probabilidad de que la variable aleatoria tome un valor menor o igual a un valor específico \(x\). Para una variable continua \(X\), la CDF \(F_X(x)\) se define como:
\[F_X(x) = P(X \leq x)\]Propiedades de la CDF en Variables Continuas
-
Continuidad: La CDF de una variable continua es una función continua en todo su dominio. Esto refleja el hecho de que no hay saltos en la probabilidad para valores específicos de \(X\).
-
Límites Asintóticos:
- \(\lim_{x \to -\infty} F_X(x) = 0\) hasta \(\lim_{x \to \infty} F_X(x) = 1\)
Estos límites indican que la CDF abarca todas las posibilidades desde la certeza de un evento no ocurriendo hasta la certeza de que ocurrirá.
- Suavidad y Derivabilidad:
- Si la variable tiene una función de densidad de probabilidad (PDF), la CDF es la integral de la PDF desde \(-\infty\) hasta \(x\).
- \(f_X(x) = F_X'(x)\), donde \(f_X(x)\) es la PDF de \(X\).
Ejemplo en Variables Continuas
Para una variable aleatoria \(X\) que sigue una distribución normal con media \(\mu\) y desviación estándar \(\sigma\), la CDF se expresa como:
\[F_X(x) = \frac{1}{2} \left[1 + \text{erf}\left(\frac{x - \mu}{\sigma \sqrt{2}}\right)\right]\]donde \(\text{erf}\) es la función de error, que surge de la normalización de la distribución normal estándar.
Función de Distribución Acumulativa (CDF) para Variables Mixtas
Las variables mixtas tienen componentes tanto continuos como discretos, haciendo que sus CDFs combinen características de ambos tipos de variables.
Características de la CDF en Variables Mixtas
- Continuidad y Discontinuidad:
- La CDF para una variable mixta es generalmente continua donde la variable es continua y tiene saltos en los puntos donde la variable toma valores discretos con probabilidad positiva.
- Saltos:
- Cada salto en la CDF corresponde a la probabilidad puntual de un valor específico de la variable mixta.
- Ejemplo en Variables Mixtas:
Supongamos que \(X\) puede tomar el valor 0 con una probabilidad de 0.2 y se distribuye uniformemente entre 1 y 2. La CDF \(F_X(x)\) sería:
- \(F_X(x) = 0\) para \(x < 0\)
- \(F_X(x) = 0.2\) para \(0 \leq x < 1\)
- \(F_X(x) = 0.2 + 0.8 \times \frac{x - 1}{1}\) para \(1 \leq x \leq 2\)
- \(F_X(x) = 1\) para \(x > 2\)
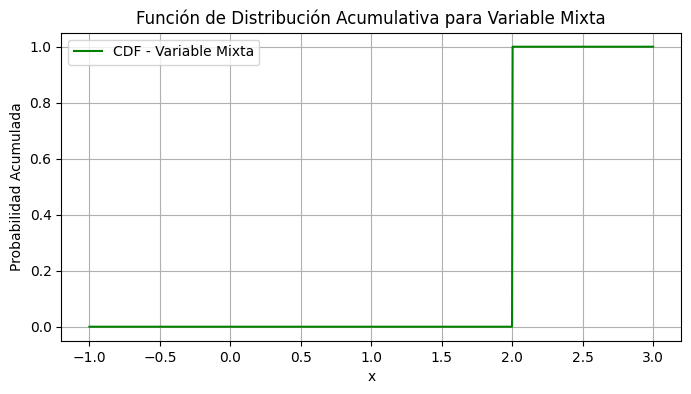
En este caso, la función tiene un salto en \(x = 0\) debido al componente discreto, y es lineal entre 1 y 2, reflejando la parte continua de la distribución.
Las CDFs son herramientas esenciales en estadística y probabilidad, facilitando la comprensión de cómo se distribuyen las variables aleatorias bajo diferentes condiciones y ayudando en la inferencia estadística y análisis de datos.
Inplamentacion con Python
Para aplicar la función de distribución acumulativa (CDF) en Python, especialmente para variables continuas y mixtas, podemos utilizar librerías como SciPy, que ofrece una amplia gama de funciones estadísticas predefinidas. Además, NumPy y Matplotlib pueden ser utilizados para manejar cálculos numéricos y visualizaciones respectivamente. A continuación, te muestro cómo implementar y visualizar CDFs para variables continuas y mixtas usando estas herramientas.
Ejemplo para Variables Continuas: Distribución Normal
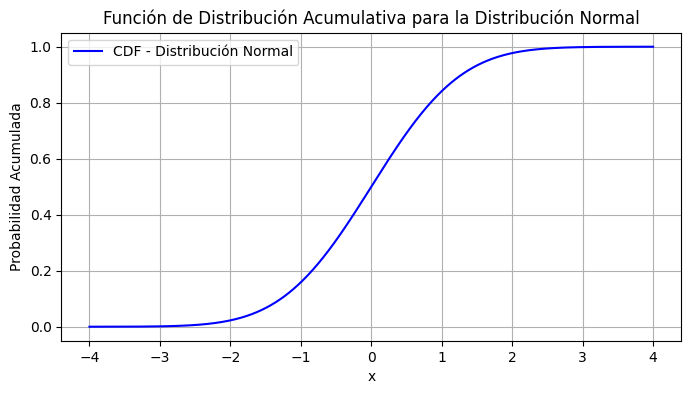
Vamos a calcular y graficar la CDF de una distribución normal estándar.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Definir los parámetros de la distribución
media = 0
desviacion_estandar = 1
# Generar valores para x
x = np.linspace(-4, 4, 1000)
# Calcular la CDF para la distribución normal
cdf_normal = norm.cdf(x, media, desviacion_estandar)
# Graficar la CDF
plt.figure(figsize=(8, 4))
plt.plot(x, cdf_normal, label='CDF - Distribución Normal', color='blue')
plt.title('Función de Distribución Acumulativa para la Distribución Normal')
plt.xlabel('x')
plt.ylabel('Probabilidad Acumulada')
plt.grid(True)
plt.legend()
plt.show()
Ejemplo para Variables Mixtas
Para demostrar el manejo de una variable mixta, consideremos un ejemplo donde la variable toma un valor discreto con cierta probabilidad y se distribuye uniformemente en otro rango. En este ejemplo, la variable toma el valor 0 con una probabilidad de 0.2 y se distribuye uniformemente entre 1 y 2.
from scipy.stats import uniform
# Definir la función CDF para una variable mixta
def cdf_mixta(x):
if x < 0:
return 0
elif 0 <= x < 1:
return 0.2
elif 1 <= x <= 2:
return 0.2 + 0.8 * (x - 1)
else:
return 1
# Generar valores para x
x_mixto = np.linspace(-1, 3, 1000)
# Calcular la CDF para cada punto x
cdf_mixto = np.vectorize(cdf_mixta)(x_mixto)
# Graficar la CDF
plt.figure(figsize=(8, 4))
plt.plot(x_mixto, cdf_mixto, label='CDF - Variable Mixta', color='green')
plt.title('Función de Distribución Acumulativa para Variable Mixta')
plt.xlabel('x')
plt.ylabel('Probabilidad Acumulada')
plt.grid(True)
plt.legend()
plt.show()
Explicación
- Librerías: Se utiliza
NumPypara manejar operaciones numéricas y crear rangos de datos,Matplotlibpara la visualización de datos, ySciPypara funciones estadísticas específicas como la CDF de la distribución normal. - CDF para Variables Mixtas: En el segundo ejemplo, definimos una función que maneja las condiciones de la variable mixta manualmente, calculando la probabilidad acumulada dependiendo del rango en el que se encuentre
x.
Estos ejemplos muestran cómo implementar y visualizar la CDF para diferentes tipos de variables en Python, lo cual es fundamental para análisis estadísticos y modelado en ciencia de datos y otras aplicaciones técnicas.
Transformacion de Variables Aleatorias
La transformación de variables aleatorias es un concepto fundamental en probabilidad y estadística que implica modificar variables aleatorias mediante una función para obtener nuevas variables con propiedades deseadas o más fáciles de analizar. Este método es esencial para simplificar problemas, realizar cálculos estadísticos y entender la distribución de datos transformados.
Si tienes una variable aleatoria \(X\) y la transformas usando una función \(g\), obtienes una nueva variable aleatoria \(Y = g(X)\). El propósito es estudiar la distribución de \(Y\) a partir del conocimiento de la distribución de \(X\) y de la función \(g\).
Métodos de Transformación
- Transformación directa:
- Si \(g\) es una función monótona (ya sea siempre creciente o siempre decreciente), entonces la función de distribución acumulativa (CDF) de \(Y\) puede ser derivada directamente de la CDF de \(X\).
- La función de densidad de probabilidad (PDF) de \(Y\), si \(X\) es una variable continua, se calcula como: \(f_Y(y) = f_X(g^{-1}(y)) \left| \frac{d}{dy}g^{-1}(y) \right|\) donde \(g^{-1}\) es la función inversa de \(g\).
- Método del cambio de variable (Transformación inversa):
- Utilizado principalmente para simular variables aleatorias según distribuciones específicas, donde eliges una función \(g\) que hace que \(Y\) tenga una distribución uniforme.
- Si \(X\) es uniforme, cualquier función inversa aplicada a \(X\) resultará en una distribución de \(Y\) que es la distribución deseada.
Ejemplos de Uso
- Normalización: Si \(X\) tiene media \(\mu\) y desviación estándar \(\sigma\), la variable \(Z = \frac{X - \mu}{\sigma}\) sigue una distribución normal estándar, útil en muchas pruebas estadísticas.
- Simulación: Las técnicas de transformación se usan en métodos de Monte Carlo para simular datos que siguen distribuciones complejas, partiendo de variables más simples como la uniforme o la normal.