Temas
Los tipos de variables aleatorias discretas se clasifican comúnmente según las distribuciones de probabilidad que describen cómo se comportan los datos asociados a estas variables.
Distribucion Binomial
La distribución binomial o distribución binómica es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de \(𝑛\) ensayos de Bernoulli independientes entre sí con una probabilidad fija \(𝑝\) de ocurrencia de éxito entre los ensayos.
La distribución binomial se utiliza con frecuencia para modelizar el número de aciertos en una muestra de tamaño \(𝑛\) extraída con reemplazo de una población de tamaño N.
Para cada experimento llamado ensayo Bernoulli, utilizamos una variable aleatoria que toma el valor 1 cuando se consigue un éxito y el valor 0 en caso contrario. La variable aleatoria, suma de todas estas variables aleatorias, cuenta el número de éxitos y sigue una distribución binomial. Es posible entonces obtener la probabilidad de \(k\) éxitos en una repetición de \(n\) experimentos:
Ejemplo Explicativo
Supongamos que lanzamos una moneda tres veces \(N = 3\), y cada lanzamiento tiene una probabilidad de 0.7 de ser cara. Los posibles resultados (espacio muestral) y la distribución de \(X\) serían:
- 0 caras (X = 0): \((Cruz, Cruz, Cruz)\)
- Probabilidad: \((1 - 0.7)^3 = 0.027\)
- 1 cara (X = 1): \((Cara, Cruz, Cruz), (Cruz, Cara, Cruz), (Cruz, Cruz, Cara)\)
- Probabilidad: \(\binom{3}{1} \times 0.7^1 \times 0.3^2 = 0.189\)
- 2 caras (X = 2): \((Cara, Cara, Cruz), (Cruz, Cara, Cara), (Cara, Cruz, Cara)\)
- Probabilidad: \(\binom{3}{2} \times 0.7^2 \times 0.3^1 = 0.441\)
- 3 caras (X = 3): \((Cara, Cara, Cara)\)
- Probabilidad: \(0.7^3 = 0.343\)
Ejemplo de Código en Python
Para trabajar con la variable aleatoria binomial en Python, una de las herramientas más útiles y comunes es el módulo numpy, específicamente la función numpy.random.binomial. Este módulo facilita la simulación de ensayos binomiales, permitiendo generar datos que siguen una distribución binomial.
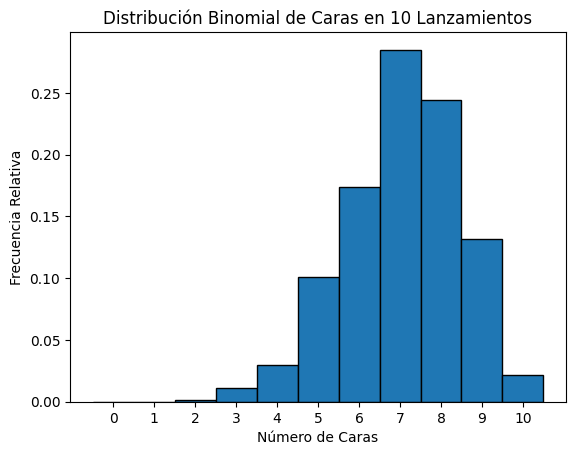
Este código utiliza la función np.random.binomial para simular 1000 ensayos binomiales donde se lanzan 10 monedas por ensayo con una probabilidad de 0.7 de obtener cara en cada lanzamiento. Luego, genera un histograma para visualizar la distribución de los resultados.
import numpy as np
import matplotlib.pyplot as plt
def simulate_binomial(n, p, trials):
"""Simula 'trials' ensayos binomiales de 'n' lanzamientos con probabilidad 'p'."""
results = np.random.binomial(n, p, trials)
return results
# Parámetros de la simulación
n = 10 # Número de lanzamientos
p = 0.7 # Probabilidad de cara
trials = 1000 # Número de simulaciones
# Realizar simulaciones
results = simulate_binomial(n, p, trials)
# Visualizar resultados
plt.hist(results, bins=np.arange(n+2)-0.5, edgecolor='black', density=True)
plt.title('Distribución Binomial de Caras en 10 Lanzamientos')
plt.xlabel('Número de Caras')
plt.ylabel('Frecuencia Relativa')
plt.xticks(range(n+1))
plt.show()
Función de Masa de Probabilidad (PMF)
Para una distribución binomial, la PMF muestra la probabilidad de que un número específico de éxitos ocurra en un número fijo de ensayos, cuando cada ensayo es independiente y tiene una probabilidad fija de éxito.
Ejemplo de Implementación en Python
Podemos usar la biblioteca scipy.stats para calcular la PMF de una distribución binomial.
from scipy.stats import binom
# Parámetros de la distribución binomial
n = 10 # Número de ensayos
p = 0.5 # Probabilidad de éxito en cada ensayo
# Número de éxitos deseado
k = 5
# Calcular la PMF para k éxitos
pmf = binom.pmf(k, n, p)
# Mostrar el resultado
print(f"PMF de {k} éxitos en {n} ensayos con p = {p}: {pmf:.4f}")
Salida:
PMF de 5 éxitos en 10 ensayos con p = 0.5: 0.2461
Interpretación de la PMF Binomial
- La PMF te permite determinar la probabilidad de que un número específico de éxitos ocurra dado un número fijo de ensayos y una probabilidad conocida de éxito.
- Es útil para modelar eventos donde hay un número finito de pruebas independientes, cada una con dos posibles resultados, como éxito/fracaso, cara/cruz, sí/no.
Visualización de la PMF
La PMF también puede ser visualizada utilizando gráficos de barras, lo que ayuda a entender cómo están distribuidas las probabilidades de diferentes cantidades de éxitos.
import matplotlib.pyplot as plt
# Crear un rango de valores k desde 0 hasta n
k_values = range(n + 1)
# Calcular la PMF para cada valor de k
pmf_values = [binom.pmf(k, n, p) for k in k_values]
# Graficar la PMF
plt.bar(k_values, pmf_values)
plt.xlabel('Número de éxitos (k)')
plt.ylabel('Probabilidad')
plt.title(f'PMF de una distribución binomial (n={n}, p={p})')
plt.show()
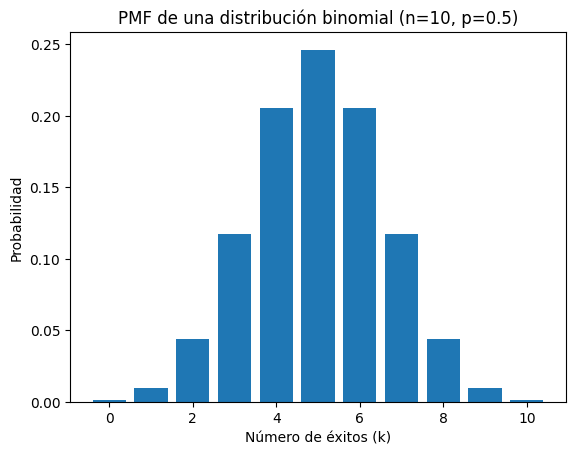
Este gráfico muestra cómo las probabilidades se distribuyen para diferentes números de éxitos posibles en una distribución binomial con parámetros específicos.
La Función de Distribución Acumulativa (CDF) para una distribución binomial muestra la probabilidad acumulada de que una variable aleatoria tome un valor menor o igual a un valor específico.
La CDF se calcula sumando las probabilidades de la Función de Masa de Probabilidad (PMF) para todos los valores desde 0 hasta \(k\).
Ejemplo de Implementación en Python
Puedes utilizar scipy.stats para calcular y visualizar la CDF de una distribución binomial.
from scipy.stats import binom
import matplotlib.pyplot as plt
# Parámetros de la distribución binomial
n = 10 # Número de ensayos
p = 0.5 # Probabilidad de éxito en cada ensayo
# Crear un rango de valores k desde 0 hasta n
k_values = range(n + 1)
# Calcular la CDF para cada valor de k
cdf_values = [binom.cdf(k, n, p) for k in k_values]
# Graficar la CDF
plt.step(k_values, cdf_values, where='mid', label=f'CDF de Binomial (n={n}, p={p})')
plt.xlabel('Número de éxitos (k)')
plt.ylabel('Probabilidad acumulada')
plt.title('Función de Distribución Acumulativa (CDF) para una Distribución Binomial')
plt.legend()
plt.grid(True)
plt.show()
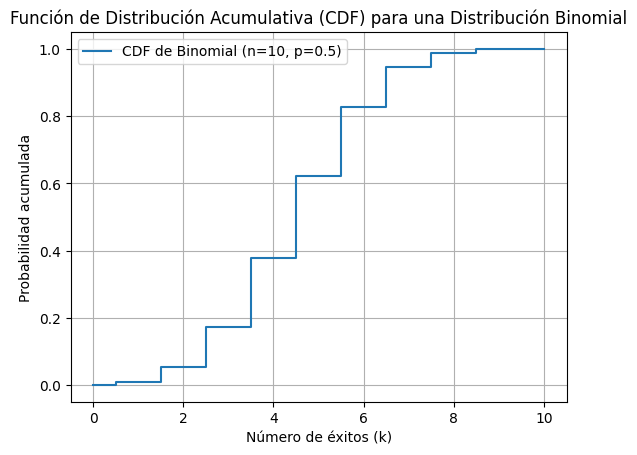
Interpretación de la CDF Binomial
La CDF binomial es útil para comprender la probabilidad acumulada de obtener hasta cierto número de éxitos en un conjunto dado de ensayos. Permite responder preguntas como “¿Cuál es la probabilidad de obtener 5 o menos éxitos?” en un experimento, y es crucial para el análisis probabilístico y la toma de decisiones en diversos campos como control de calidad, finanzas, investigación biomédica, entre otros.
Distribución de Poisson
La distribución de Poisson se utiliza para describir la cantidad de veces que ocurre un determinado evento dentro de un intervalo de tiempo o espacio fijo. Por ejemplo, la distribución de Poisson se puede utilizar para describir la cantidad de automóviles que pasan por una intersección específica entre las 4 p.m. y las 5 p.m. de un día determinado. También se puede utilizar para describir la cantidad de llamadas recibidas en una oficina entre las 13:00 y las 15:00 horas de un día determinado.
La distribución de Poisson está definida por el parámetro de tasa, simbolizado por la letra griega lambda, λ.
Lambda representa el valor esperado (o el valor promedio) de la distribución. Por ejemplo, si nuestro número esperado de clientes entre la 1:00 p.m. y las 2:00 p.m. es 7, entonces estableceríamos el parámetro para la distribución de Poisson en 7. El PMF para la distribución de Poisson(7) es el siguiente:
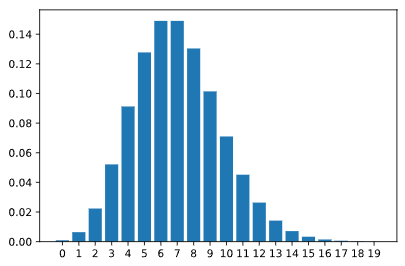
¿Cómo se ve la PMF de la distribución de Poisson con diferentes valores en el parámetro lambda?
Utilice el control deslizante del subprograma para ver cómo cambia la distribución de la función de masa de probabilidad a medida que lambda cambia entre 1 y 10. La altura de las barras representa la probabilidad de observar el número a lo largo del eje x. Puede pasar el cursor sobre cualquier barra específica y ver la probabilidad específica de ese valor.
Calcular probabilidades de valores exactos utilizando la función de masa de probabilidad
La distribución de Poisson es una distribución de probabilidad discreta, por lo que puede describirse mediante una función de masa de probabilidad y una función de distribución acumulativa.
Podemos usar el método poisson.pmf() en la biblioteca scipy.stats para evaluar la probabilidad de observar un número específico dado el parámetro (valor esperado) de una distribución.
Por ejemplo, supongamos que esperamos que llueva 10 veces en los próximos 30 días. El número de veces que llueve en los próximos 30 días tiene “distribución de Poisson” con lambda = 10. Podemos calcular la probabilidad de que llueva exactamente 6 veces de la siguiente manera:
import scipy.stats as stats
# expected value = 10, probability of observing 6
stats.poisson.pmf(6, 10)
Output
0.06305545800345125
Al igual que las funciones de masa de probabilidad anteriores de variables aleatorias discretas, las probabilidades individuales se pueden sumar para encontrar la probabilidad de observar un valor en un rango.
Por ejemplo, si esperamos que llueva 10 veces en los próximos 30 días, el número de veces que llueve en los próximos 30 días tiene una “distribución de Poisson” con lambda = 10. Podemos calcular la probabilidad de que llueva entre 12 y 14 veces. como sigue:
import scipy.stats as stats
# expected value = 10, probability of observing 12-14
stats.poisson.pmf(12, 10)
+ stats.poisson.pmf(13, 10)
+ stats.poisson.pmf(14, 10)
Output
0.21976538076223123
Calcular probabilidades de un rango usando la función de densidad acumulativa
Podemos usar el método poisson.cdf() en la biblioteca scipy.stats para evaluar la probabilidad de observar un número específico o menos dado el valor esperado de una distribución. Por ejemplo, si quisiéramos calcular la probabilidad de observar 6 o menos eventos de lluvia en los próximos 30 días cuando esperábamos 10, podríamos hacer lo siguiente:
import scipy.stats as stats
# expected value = 10, probability of observing 6 or less
stats.poisson.cdf(6, 10)
Output
0.130141420882483
Esto significa que hay aproximadamente un 13% de posibilidades de que haya 6 lluvias o menos en el mes en cuestión.
También podemos utilizar este método para evaluar la probabilidad de observar un número específico o más dado el valor esperado de la distribución. Por ejemplo, si quisiéramos calcular la probabilidad de observar 12 o más eventos de lluvia en los próximos 30 días cuando esperábamos 10, podríamos hacer lo siguiente:
import scipy.stats as stats
# expected value = 10, probability of observing 12 or more
1 - stats.poisson.cdf(11, 10)
Output
0.30322385369689386
Esto significa que hay aproximadamente un 30% de posibilidades de que haya 12 o más lluvias en el mes en cuestión.
Tenga en cuenta que utilizamos 11 en la declaración anterior a pesar de que 12 era el valor dado en el mensaje. Queríamos calcular la probabilidad de observar 12 o más lluvias, lo que incluye 12. stats.poisson.cdf(11, 10) Evalúa la probabilidad de observar 11 o menos lluvias, por lo que 1 - stats.poisson.cdf(11, 10) sería igual a la probabilidad de observar 12 o más lluvias.
Sumar probabilidades individuales en un amplio rango puede resultar engorroso. A menudo es más fácil calcular la probabilidad de un rango utilizando la función de densidad acumulada en lugar de la función de masa de probabilidad. Podemos hacer esto tomando la diferencia entre la CDF del punto final más grande y la CDF de uno menos que el punto final más pequeño del rango.
Por ejemplo, aunque todavía esperamos 10 lluvias en los próximos 30 días, podríamos usar el siguiente código para calcular la probabilidad de observar entre 12 y 18 eventos de lluvia:
import scipy.stats as stats
# expected value = 10, probability of observing between 12 and 18
stats.poisson.cdf(18, 10) - stats.poisson.cdf(11, 10)
Output
0.29603734909303947
Expectativa de la distribución de Poisson
Anteriormente mencionamos que el parámetro lambda (λ) es el valor esperado (o valor promedio) de la distribución de Poisson. Pero ¿qué significa esto?
Pongamos esto en contexto: digamos que somos vendedores, y después de muchas semanas de trabajo, calculamos que nuestro promedio es de 10 ventas por semana. Si tomamos este valor como nuestro valor esperado de una distribución de Poisson, la función de masa de probabilidad tendrá el siguiente aspecto:
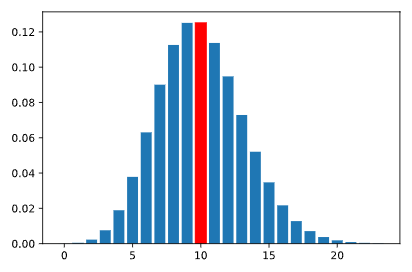
La barra más alta representa el valor con mayor probabilidad de ocurrir. En este caso, la barra más alta está en 10. Sin embargo, esto no significa que realizaremos 10 ventas. Significa que, en promedio, en todas las semanas, esperamos que nuestro promedio sea de aproximadamente 10 ventas por semana.
Miremos esto de otra manera. Tomemos una muestra de 1000 valores aleatorios de la distribución de Poisson con el valor esperado de 10. Podemos usar el método poisson.rvs() en la biblioteca scipy.stats para generar valores aleatorios:
import scipy.stats as stats
# generate random variable
# stats.poisson.rvs(lambda, size = num_values)
rvs = stats.poisson.rvs(10, size = 1000)
El histograma de este muestreo se parece al siguiente:
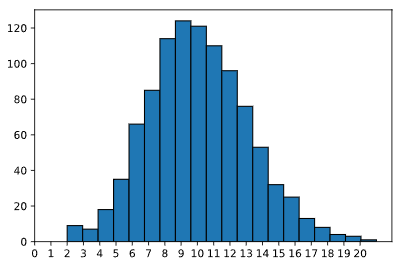
Podemos ver observaciones tan bajas como 2 pero tan altas como 20. Las barras más altas están en 9 y 10. Si tomáramos el promedio de las 1000 muestras aleatorias, obtendríamos:
print(rvs.mean())
Output:
10.009
Este valor está muy cerca de 10, lo que confirma que sobre las 1000 observaciones, el valor esperado (o promedio) es 10.
Cuando hablamos del valor esperado, nos referimos al promedio de muchas observaciones. Esto se relaciona con la Ley de los Grandes Números: cuantas más muestras tengamos, es más probable que las muestras se parezcan a la población real y la media de las muestras se acerque al valor esperado. Entonces, aunque el vendedor pueda realizar 3 ventas una semana, puede realizar 16 la siguiente y 11 la semana siguiente. A largo plazo, después de muchas semanas, el valor esperado (o promedio) seguiría siendo 10.
Propagación de la distribución de Poisson
Las distribuciones de probabilidad también tienen varianzas calculables. Las varianzas son una forma de medir la dispersión de valores y probabilidades en la distribución. Para la distribución de Poisson, la varianza es simplemente el valor de lambda (λ), lo que significa que el valor esperado y la varianza son equivalentes en las distribuciones de Poisson.
Sabemos que la distribución de Poisson tiene una variable aleatoria discreta y debe ser mayor que 0 (piense, un vendedor no puede tener menos de 0 ventas, una tienda no puede tener menos de 0 clientes), por lo que a medida que aumenta el valor esperado, el número de posibles Los valores que la distribución puede asumir también aumentarían.
El primer gráfico a continuación muestra una distribución de Poisson con lambda igual a tres, y el segundo gráfico muestra una distribución de Poisson con lambda igual a quince. Observe que en el segundo gráfico, la dispersión de la distribución aumenta. Además, tenga en cuenta que la altura de las barras en la segunda barra disminuye ya que hay más valores posibles en la distribución.
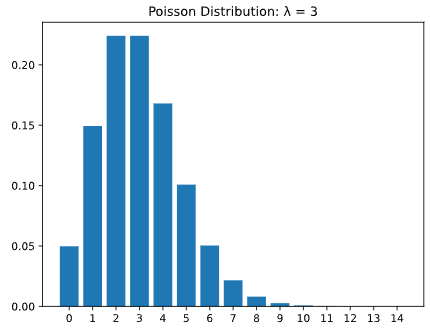
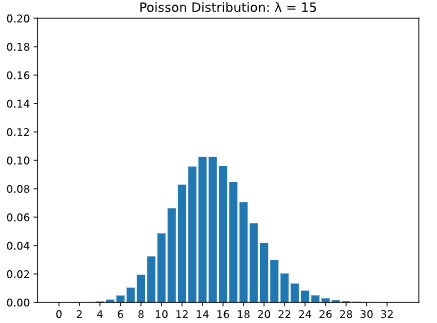
Como podemos ver, a medida que aumenta el parámetro lambda, también aumenta la varianza (o dispersión) de los valores posibles.
Podemos calcular la varianza de una muestra usando el método numpy.var():
import scipy.stats as stats
import numpy as np
rand_vars = stats.poisson.rvs(4, size = 1000)
print(np.var(rand_vars))
Output:
3.864559
Debido a que esto se calcula a partir de una muestra, es posible que la varianza no sea EXACTAMENTE igual a lambda. Sin embargo, esperamos que sea relativamente cercano cuando el tamaño de la muestra es grande, como en este ejemplo.
Otra forma de ver el aumento de los valores posibles es tomar el rango de una muestra (los valores mínimo y máximo de un conjunto). El siguiente código extraerá 1000 variables aleatorias de la distribución de Poisson con lambda = 4 y luego imprimirá los valores mínimo y máximo observados usando las funciones .min() y .max() de Python:
import scipy.stats as stats
rand_vars = stats.poisson.rvs(4, size = 1000)
print(min(rand_vars), max(rand_vars))
Output:
0 12
Si aumentamos el valor de lambda a 10, veamos cómo cambian los valores mínimo y máximo:
import scipy.stats as stats
rand_vars = stats.poisson.rvs(10, size = 1000)
print(min(rand_vars), max(rand_vars))
Output:
1 22
Estos valores están más distribuidos, lo que indica una variación mayor.
Distribucion Geometrica
La distribución geométrica es una distribución de probabilidad discreta que describe el número de intentos necesarios para lograr el primer éxito en una serie de ensayos independientes, cada uno con una probabilidad constante de éxito. Es una distribución discreta porque el número de intentos es un valor entero.
Ensayos Independientes de Bernoulli
Un ensayo independiente implica que el resultado de un ensayo que no influye ni puede ser influenciado por los resultados de otros ensayos. En el contexto de lanzar una moneda, significa que el resultado de un lanzamiento no afecta el resultado del siguiente.
Ejemplo con Dos Lanzamientos
Si lanzamos una moneda dos veces con una probabilidad de 0.7 de sacar cara en cada lanzamiento, la probabilidad de obtener dos caras seguidas sería \(0.7 \times 0.7 = 0.49\).
Explicación y Ejemplo
Supongamos que lanzamos una moneda hasta que salga cara por primera vez, y queremos saber cuántos lanzamientos se necesitan.
def geometric_trial(p=0.7):
"""Simula una variable aleatoria geométrica.
Args:
p (float): Probabilidad de sacar cara.
Returns:
int: Número de lanzamientos hasta el primer éxito.
"""
count = 1
while bernoulli_trial(p) == 0:
count += 1
return count
Esta función utiliza la función de Bernoulli definida anteriormente para simular lanzamientos sucesivos hasta que el primer lanzamiento resulte en éxito (cara).
Función de Masa de Probabilidad (PMF) de la Variable Geométrica
La PMF de una variable aleatoria geométrica da la probabilidad de que se necesite un número específico de ensayos para alcanzar el primer éxito.
Ejemplo
- \(P(X=1) = 0.7\) (sacar cara en el primer lanzamiento).
- \(P(X=2) = 0.3 \times 0.7\) (sacar cruz en el primero y cara en el segundo).
- \(P(X=n) = 0.3^{(n-1)} \times 0.7\) (sacar cruz en los primeros \(n-1\) lanzamientos y cara en el \(n\)-ésimo).
Prueba de normalización de variable aleatoria geométrica opcional
Este segmento explica la variable aleatoria geométrica en detalle, destacando su importancia en el contexto de ensayos independientes de Bernoulli, como el lanzamiento repetido de una moneda hasta obtener el primer éxito (cara). Además, se aborda la propiedad de normalización de la distribución geométrica y se anticipa una demostración práctica utilizando Python. Vamos a desglosar y ampliar estos conceptos y ejemplos en español.
Variable Aleatoria Geométrica
La variable aleatoria geométrica mide el número de intentos necesarios hasta obtener el primer éxito en una serie de ensayos independientes de Bernoulli. Por ejemplo, en el lanzamiento de una moneda, esta variable contaría cuántos lanzamientos se realizan hasta que aparece la primera cara, asumiendo que cada lanzamiento es independiente del anterior.
Propiedades de la Variable Geométrica
- Espacio Muestral Infinito pero Contable: La variable geométrica puede tomar una cantidad infinita de valores (1, 2, 3, …), ya que teóricamente podrían requerirse infinitos lanzamientos para obtener una cara. Sin embargo, estos valores son contables, lo que clasifica a la variable como discreta.
- Distribución de Probabilidad: La probabilidad de que la variable aleatoria geométrica tome un valor específico \(k\) es una función de la probabilidad de éxito \(p\) y la probabilidad de fracaso \(q = 1-p\). donde \(k\) es el número de lanzamientos realizados hasta obtener el primer éxito.
Aplicación Práctica en Python
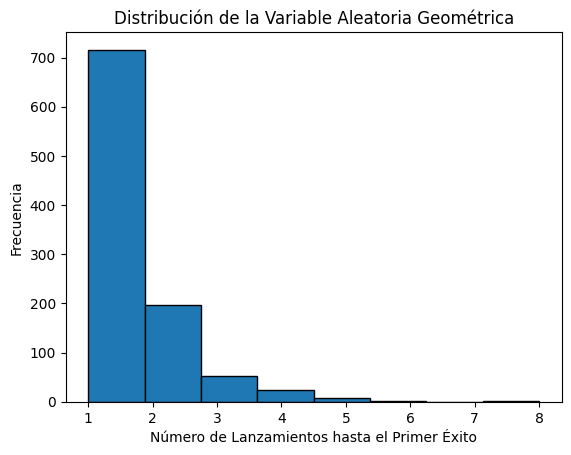
Este código simula 1000 ensayos de una variable aleatoria geométrica y utiliza un histograma para visualizar cuántos lanzamientos se necesitan típicamente para obtener el primer éxito. Esta visualización ayuda a comprender la naturaleza de la distribución geométrica y la efectividad de los ensayos de Bernoulli independientes.
import numpy as np
import matplotlib.pyplot as plt
def geometric_trial(p=0.7):
count = 0
while np.random.rand() >= p:
count += 1
return count + 1
# Simulación de 1000 ensayos geométricos
results = [geometric_trial(p=0.7) for _ in range(1000)]
# Visualización de la distribución
plt.hist(results, bins=max(results), edgecolor='black')
plt.title('Distribución de la Variable Aleatoria Geométrica')
plt.xlabel('Número de Lanzamientos hasta el Primer Éxito')
plt.ylabel('Frecuencia')
plt.show()