Correlacion: dos variables cuantitativas
Cuando existen asociaciones entre variables, significa que la información sobre el valor de una variable nos da información sobre el valor de la otra variable. En esta lección, cubriremos formas de examinar una asociación entre dos variables cuantitativas.
A lo largo de los próximos ejercicios, examinaremos algunos datos sobre alquileres de viviendas en Texas en Craigslist, un sitio de anuncios clasificados en línea. El diccionario de datos es el siguiente:
price: precio de alquiler mensual en USDtype: tipo de vivienda (p. ej., ‘apartment’, - ‘house’, ‘condo’, etc.)sqfeet: área de vivienda, en pies cuadradosbeds: número de camasbaths: número de bañoslat: latitudlong: longitud
Excepto type, todas estas variables son cuantitativas. ¿Qué pares de variables crees que podrían estar asociados? Por ejemplo, ¿saber algo sobre el precio le proporciona alguna información sobre los metros cuadrados?
Gráfico de dispersión
Una de las mejores formas de visualizar rápidamente la relación entre variables cuantitativas es compararlas entre sí en un diagrama de dispersión. Esto facilita la búsqueda de patrones o tendencias en los datos. Comencemos trazando el área de un alquiler con respecto a su precio mensual para ver si podemos detectar algún patrón.
plt.scatter(x = housing.price, y = housing.sqfeet)
plt.xlabel('Rental Price (USD)')
plt.ylabel('Area (Square Feet)')
plt.show()
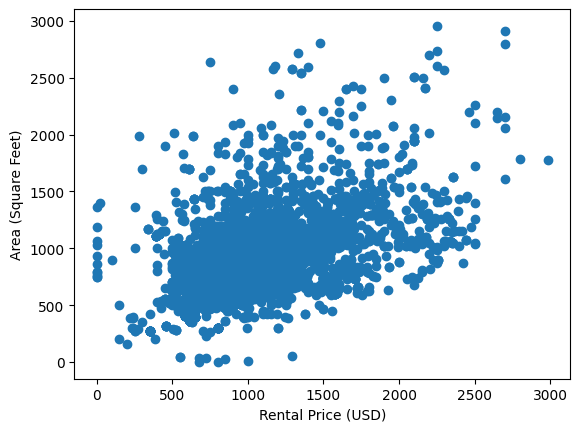
Si bien hay mucha variación en los datos, parece que las viviendas más caras tienden a tener un poco más de espacio. Esto sugiere una asociación entre estas dos variables.
Es importante señalar que diferentes tipos de asociaciones pueden conducir a diferentes patrones en un diagrama de dispersión. Por ejemplo, el siguiente gráfico muestra la relación entre la edad de un niño en meses y su peso en libras. Podemos ver que los niños mayores tienden a pesar más pero que la tasa de crecimiento comienza a estabilizarse después de los 36 meses:
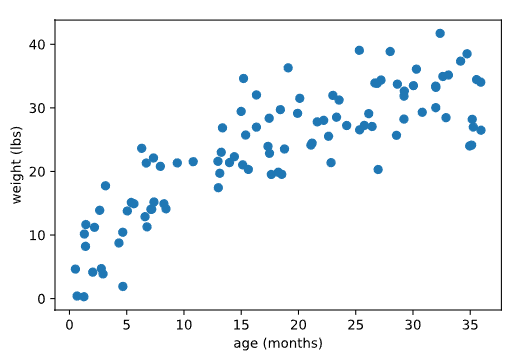
Si no vemos ningún patrón en un diagrama de dispersión, probablemente podamos suponer que las variables no están asociadas. Por ejemplo, un diagrama de dispersión como este no sugeriría ninguna asociación:
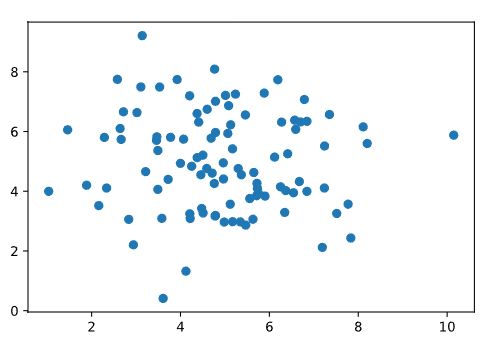
Explorando la covarianza
Más allá de visualizar relaciones, también podemos utilizar estadísticas resumidas para cuantificar la fuerza de ciertas asociaciones. La covarianza es una estadística resumida que describe la fuerza de una relación lineal. Una relación lineal es aquella en la que una línea recta describiría mejor el patrón de puntos en un diagrama de dispersión.
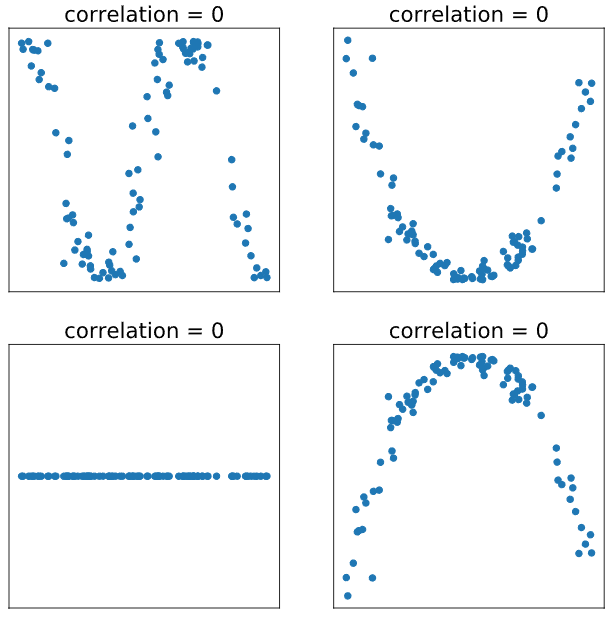
La covarianza puede variar desde infinito negativo hasta infinito positivo. Una covarianza positiva indica que un valor mayor de una variable está asociado con un valor mayor de la otra. Una covarianza negativa indica que un valor mayor de una variable está asociado con un valor menor de la otra. Una covarianza de 0 indica que no hay relación lineal. Aquí hay unos ejemplos:
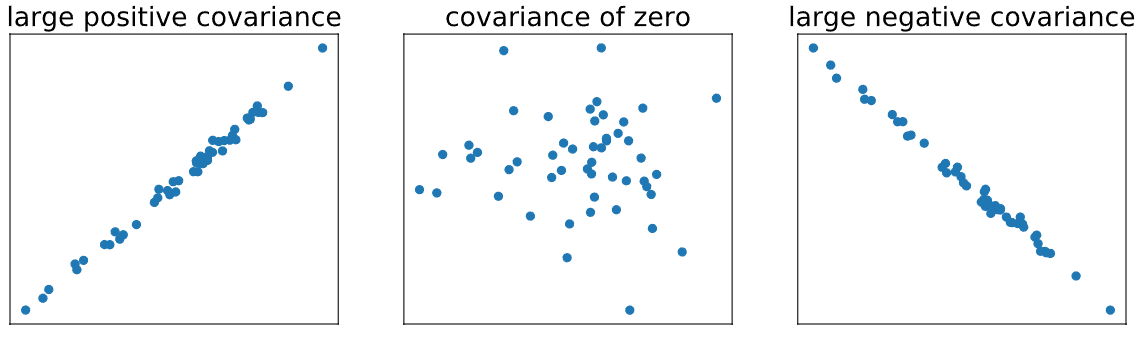
Para calcular la covarianza, podemos usar la función cov() de NumPy, que produce una matriz de covarianza para dos o más variables . Una matriz de covarianza para dos variables se parece a esto:
| Variable 1 | Variable 2 | |
|---|---|---|
| Variable 1 | varianza (Variable 1) | covarianza |
| Variable 2 | covarianza | varianza (Variable 2) |
En Python, podemos calcular esta matriz de la siguiente manera:
cov_mat_price_sqfeet = np.cov(housing.price, housing.sqfeet)
print(cov_mat_price_sqfeet)
# output:
[[184332.9 57336.2]
[ 57336.2 122045.2]]
Observe que la covarianza aparece dos veces en esta matriz y es igual a 57336.2. Para guardarla:
cov_sqfeet_beds = cov_mat_sqfeet_beds[1][0]
Correlación
Al igual que la covarianza, la correlación de Pearson (a menudo denominada simplemente “correlación”) es una forma escalada de covarianza. También mide la fuerza de una relación lineal, pero oscila entre -1 y +1, lo que la hace más interpretable.
Las variables altamente asociadas con una relación lineal positiva tendrán una correlación cercana a 1. Las variables altamente asociadas con una relación lineal negativa tendrán una correlación cercana a -1. Las variables que no tienen una asociación lineal (o una asociación lineal con pendiente cero) tendrán correlaciones cercanas a 0.
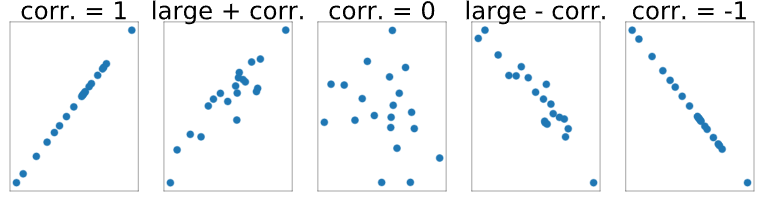
La función pearsonr() de scipy.stats se puede utilizar para calcular la correlación de la siguiente manera:
corr_price_sqfeet, p = pearsonr(housing.price, housing.sqfeet)
# output
0.5070065351127468
Generalmente, una correlación mayor que aproximadamente 0,3 indica una asociación lineal. Una correlación superior a aproximadamente 0,6 sugiere una fuerte asociación lineal.
Es importante señalar que existen algunas limitaciones al utilizar la correlación o la covarianza como forma de evaluar si existe una asociación entre dos variables . Dado que tanto la correlación como la covarianza miden la fuerza de las relaciones lineales con pendientes distintas de cero, pero no otros tipos de relaciones, la correlación puede ser engañosa.
Por ejemplo, los cuatro diagramas de dispersión siguientes muestran pares de variables con correlaciones cercanas a cero. La imagen inferior izquierda muestra un ejemplo de una asociación lineal perfecta donde la pendiente es cero (la línea es horizontal). Mientras tanto, los otros tres gráficos muestran relaciones no lineales: si trazáramos una línea a través de cualquiera de estos conjuntos de puntos, ¡esa línea tendría que ser curva, no recta!