Correlación
En este capítulo, exploraremos la correlación entre diferentes factores y estimaremos hasta qué punto estos diferentes factores son confiables. Además, aprenderemos sobre los diferentes tipos de exámenes que podemos realizar para descubrir la relación entre los datos, incluido el análisis univariado, el análisis bivariado y el análisis multivariado.
Introduccion
Cualquier conjunto de datos que queramos analizar tendrá diferentes campos (es decir, columnas) de múltiples observaciones (es decir, variables) que representan diferentes hechos. Lo más probable es que las columnas de un conjunto de datos estén relacionadas entre sí porque se recopilan del mismo evento. Un campo de registro puede afectar o no el valor de otro campo. Para examinar el tipo de relaciones que tienen estas columnas y analizar las causas y efectos entre ellas, tenemos que trabajar para encontrar las dependencias que existen entre las variables. La fuerza de dicha relación entre dos campos de un conjunto de datos se llama correlación , que está representada por un valor numérico entre -1 y 1.
En otras palabras, la técnica estadística que examina la relación y explica si, y en qué medida, los pares de variables están relacionados entre sí se conoce como correlación. La correlación responde a preguntas como cómo cambia una variable con respecto a otra. Si cambia, ¿en qué grado o fuerza? Además, si la relación entre esas variables es lo suficientemente fuerte, entonces podemos hacer predicciones sobre el comportamiento futuro.
Por ejemplo, la altura y el peso están relacionados; es decir, las personas más altas tienden a pesar más que las personas más bajas. Si tenemos una nueva persona que es más alta que la altura promedio que observamos antes, entonces es más probable que pese más que el peso promedio que observamos.
La correlación nos dice cómo las variables cambian juntas, tanto en la misma dirección como en direcciones opuestas, y en la magnitud (es decir, la fuerza) de la relación. Para encontrar la correlación, calculamos el coeficiente de correlación de Pearson, simbolizado por ρ (la letra griega rho ). Esto se obtiene dividiendo la covarianza por el producto de las desviaciones estándar de las variables:
pxy = oxy / oxoy
En términos de fuerza de la relación, el valor de la correlación entre dos variables, A y B , varía entre +1 y -1.
- Si la correlación es +1, entonces se dice que es una correlación positiva/lineal perfecta (es decir, la variable A es directamente proporcional a la variable B).
- Mientras que una correlación de -1 es una correlación negativa perfecta (es decir, la variable A es inversamente proporcional a la variable B). Tenga en cuenta que se supone que los valores más cercanos a 0 no están correlacionados en absoluto.
- Si los coeficientes de correlación están cerca de 1 en valor absoluto, entonces se dice que las variables están fuertemente correlacionadas;
- en comparación, se dice que aquellos que están más cerca de 0,5 están débilmente correlacionados.
Echemos un vistazo a algunos ejemplos que utilizan diagramas de dispersión. Los diagramas de dispersión muestran cuánto se ve afectada una variable por otra:
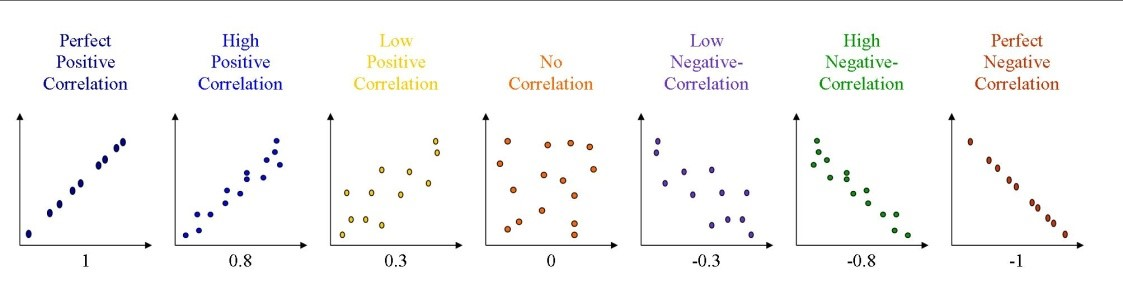
Como se muestra en el primer y último gráfico, cuanto más cercana sea la distancia entre los puntos de datos cuando se trazan para formar una línea recta, mayor será la correlación entre las variables asociadas. Cuanto mayor sea la correlación entre ellas, más fuerte será la relación entre las variables. Cuanto más dispersos se vuelven los puntos de datos cuando se trazan (por lo tanto, no se crean patrones), menor es la correlación entre las dos variables. Aquí, debes observar los siguientes cuatro puntos importantes:
- Cuando la gráfica de puntos de datos tiene una línea recta que pasa por el origen hasta los valores xey , entonces se dice que las variables tienen una correlación positiva .
- Cuando los puntos de datos se trazan para generar una línea que va desde un valor alto en el eje y a un valor alto en el eje x , se dice que las variables tienen una correlación negativa .
- Una correlación perfecta tiene un valor de 1.
- Una correlación negativa perfecta tiene un valor de -1.
A una correlación altamente positiva se le asigna un valor más cercano a 1. A una correlación altamente negativa se le asigna un valor más cercano a -1. En el diagrama anterior, +0,8 da una correlación positiva alta y -0,8 da una correlación negativa alta. Cuanto más cerca
La correlación no implica causa
La correlación no implica causalidad es una frase interesante que escuchará principalmente en estadística y cuando aprenda en detalle sobre ciencia de datos. Pero, ¿qué significa? Bueno, simplemente indica que el hecho de que dos cosas se correlacionen no siempre significa que una cause la otra. Por ejemplo, el invierno noruego es frío y la gente tiende a gastar más dinero en comprar alimentos calientes, como sopa, que en verano. Sin embargo, esto no significa que el clima frío haga que la gente gaste más dinero en sopa. Por lo tanto, aunque el gasto de la gente en Noruega está relacionado con el clima frío, el gasto no es la causa del clima frío. Por tanto, la correlación no es causalidad.
Tenga en cuenta que hay dos términos esenciales en esta frase: correlación y causalidad. La correlación revela cuán fuertemente se relacionan entre sí y cambian juntas las apariencias de las variables. La causalidad explica que cualquier cambio en el valor de una variable provocará una diferencia en la cantidad de otra variable. En este caso, una variable hace que suceda la otra variable. Este fenómeno se conoce como causa y efecto . Por ejemplo, cuando haces ejercicio ( X ), la cantidad de calorías ( Y ) que quemas es mayor cada minuto. Por tanto , X causa Y.
El ejemplo más común que se encuentra en cualquier libro de análisis de datos es el de las ventas de helados y el aumento y caída de los homicidios. Según este ejemplo, a medida que aumenta la venta de helados, aumenta el número de homicidios. Según la correlación, estos dos eventos están altamente correlacionados. Sin embargo, el consumo de helado no está provocando la muerte de personas. Estas dos cosas no se basan en la teoría de causa y efecto. Por tanto, correlación no significa causalidad.
Entonces, ¿cuál es la conclusión de esta frase crítica? Bueno, en primer lugar, no debemos sacar conclusiones demasiado rápido basándose en la correlación. Es esencial invertir algo de tiempo en encontrar los factores subyacentes de los datos para comprender los factores críticos ocultos.
Análisis Bivariado
Como su nombre indica, se trata del análisis de más de un (es decir, exactamente dos) tipo de variable. El análisis bivariado se utiliza para saber si existe una relación entre dos variables diferentes. Cuando creamos un diagrama de dispersión trazando una variable frente a otra en un plano cartesiano (piense en los ejes x e y), nos da una idea de lo que los datos intentan decirnos. Si los puntos de datos parecen ajustarse a la línea o curva, entonces existe una relación o correlación entre las dos variables. Generalmente, el análisis bivariado nos ayuda a predecir un valor para una variable (es decir, una variable dependiente) si conocemos el valor de la variable independiente.
A continuación se muestra un diagrama que muestra un diagrama de dispersión de los dólares en publicidad y las tasas de ventas durante un período de tiempo:
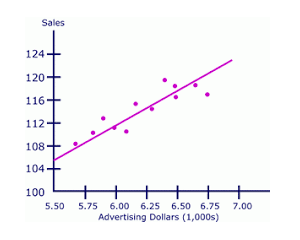
Este diagrama es el diagrama de dispersión para el análisis bivariado, donde los dólares de ventas y publicidad son dos variables. Al trazar un diagrama de dispersión, podemos ver que los valores de las ventas dependen de los dólares de publicidad; es decir, a medida que aumentan los dólares de publicidad, también aumentan los valores de ventas. Esta comprensión de la relación entre dos variables nos guiará en nuestras predicciones futuras:
Análisis multivariado
El análisis multivariado es el análisis de tres o más variables. Esto nos permite observar las correlaciones (es decir, cómo cambia una variable con respecto a otra) e intentar hacer predicciones para el comportamiento futuro con mayor precisión que con el análisis bivariado.