Temas
- Variables aleatorias discretas
- Función de Masa de Probabilidad (PMF)
- Función de distribución acumulativa
- Tipos de Variables Aleatorias Discretas
- Variables aleatorias continuas
- Funcion de densidad de probabilidad
Variables Aleatorias
Las variables aleatorias son un concepto central en la teoría de la probabilidad y estadística, representando cantidades que resultan de un experimento aleatorio y cuyos valores no son predecibles con certeza antes de realizar el experimento. Estas variables pueden clasificarse en dos grandes categorías: variables aleatorias discretas y variables aleatorias continuas.
Una variable aleatoria puede ser entendida como una función que asigna un valor numérico a cada resultado de un espacio muestral asociado con un experimento aleatorio. Por ejemplo, si lanzas un dado, el resultado (número de puntos hacia arriba) es el valor que toma la variable aleatoria.
Variables aleatorias discretas
Las variables aleatorias discretas son aquellas que toman un número finito o contablemente infinito de valores distintos. Cada uno de estos valores tiene una probabilidad asociada, y la suma de todas estas probabilidades debe ser igual a uno. Este tipo de variable es muy común en la estadística y la teoría de la probabilidad, y se utiliza frecuentemente para modelar situaciones donde los resultados son claramente separables y contables. Pueden adoptar valores que se pueden contar, como 0, 1, 2, …, n, o una lista de valores específicos como {-3, -1, 0, 1, 5}.
Variable Aleatoria de Bernoulli
Una variable aleatoria de Bernoulli es un tipo específico de variable aleatoria discreta que sólo toma dos posibles valores, típicamente 0 y 1, para representar los resultados de un único ensayo de Bernoulli. Este tipo de variable es fundamental en probabilidad y estadística para modelar el resultado de experimentos que tienen exactamente dos posibles resultados, comúnmente etiquetados como “éxito” y “fracaso”.
Definición
Una variable de Bernoulli \(X\) se define de la siguiente manera:
- \(X = 1\) con probabilidad \(p\) (éxito).
- \(X = 0\) con probabilidad \(1-p\) (fracaso).
Ejemplo con la Suma de Dos Dados
Si consideramos la variable \(S\) como la suma de dos lanzamientos de un dado:
- \(P(S = 2) = \frac{1}{36}\) porque solo hay una forma de obtener un 2: lanzando dos unos.
- \(P(S = 3) = \frac{2}{36}\) porque hay dos combinaciones que dan un 3: (1,2) y (2,1).
- Y así sucesivamente hasta \(S = 12\).
Estos cálculos asumen que todos los resultados son igualmente probables, lo cual es cierto para un dado justo.
Aplicación Práctica: Variable Aleatoria Bernoulli
Una variable aleatoria Bernoulli es un tipo especial de variable aleatoria discreta que solo toma dos valores, generalmente 0 y 1. Es extremadamente útil para modelar experimentos binarios como el lanzamiento de una moneda.
Ejemplo con el Lanzamiento de una Moneda
- Si la moneda es justa, \(P(X = 1) = 0.5\) y \(P(X = 0) = 0.5\).
- Si la moneda no es justa y la probabilidad de cara es 0.7, entonces \(P(X = 1) = 0.7\) y \(P(X = 0) = 0.3\).
La PMF en este caso asignaría 0.7 a obtener cara y 0.3 a obtener cruz, reflejando la naturaleza sesgada de la moneda.
Simulación en Python
Vamos a construir una función en Python que simule un experimento de Bernoulli, el cual podría representar, por ejemplo, el lanzamiento de una moneda:
import numpy as np
def bernoulli_trial(p=0.5):
"""Simula un experimento de Bernoulli.
Args:
p (float): Probabilidad de éxito (por defecto 0.5).
Returns:
int: 1 si el experimento resulta en éxito, 0 en caso contrario.
"""
return 1 if np.random.rand() <= p else 0
En esta función, np.random.rand() genera un número aleatorio entre 0 y 1, y compara este número con la probabilidad de éxito p. Si el número generado es menor o igual a p, el resultado es un éxito (1); de lo contrario, es un fracaso (0).
Simulación y Análisis de Resultados
Podemos usar esta función para realizar múltiples ensayos y observar la frecuencia de éxitos, lo que nos permite estimar la probabilidad de éxito de la moneda:
def simulate_bernoulli_trials(n, p=0.5):
"""Simula n ensayos de Bernoulli y reporta la frecuencia de éxitos.
Args:
n (int): Número de ensayos.
p (float): Probabilidad de éxito.
Returns:
float: Frecuencia de éxitos.
"""
results = [bernoulli_trial(p) for _ in range(n)]
return sum(results) / n
# Simular 1000 lanzamientos de una moneda con p = 0.7
n_trials = 1000
success_prob = 0.612199
frequency_of_success = simulate_bernoulli_trials(n_trials, success_prob)
print(f"La frecuencia de éxito estimada es {frequency_of_success:.2f}")
Output:
La frecuencia de éxito estimada es 0.71
Este código simula 1000 lanzamientos de una moneda donde la probabilidad de obtener cara (éxito) es del 70%. La función simulate_bernoulli_trials devuelve la frecuencia de éxitos, que debería acercarse a 0.7 a medida que el número de ensayos aumenta.
Visualización de la Convergencia
Para visualizar cómo la frecuencia de éxitos converge a la probabilidad real, podríamos realizar múltiples simulaciones aumentando progresivamente el número de ensayos y graficar los resultados:
import matplotlib.pyplot as plt
trial_counts = [10, 50, 100, 500, 1000, 5000, 10000]
frequencies = [simulate_bernoulli_trials(count, success_prob) for count in trial_counts]
plt.figure(figsize=(10, 5))
plt.plot(trial_counts, frequencies, marker='o', linestyle='-')
plt.axhline(y=success_prob, color='r', linestyle='--')
plt.title('Convergencia de la Frecuencia de Éxitos a la Probabilidad Real')
plt.xlabel('Número de Ensayos')
plt.ylabel('Frecuencia de Éxitos')
plt.xscale('log')
plt.show()
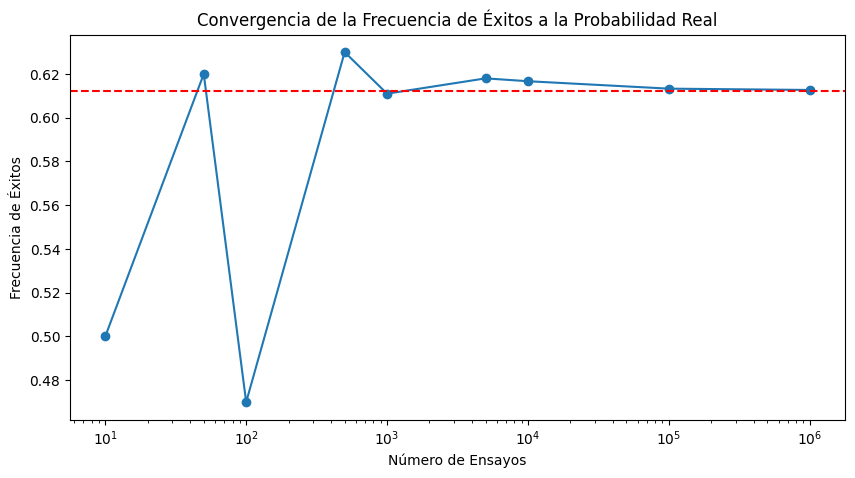
Este gráfico mostrará cómo la frecuencia de éxitos se estabiliza y converge hacia la probabilidad real de éxito (0.612199 en este caso) a medida que aumenta el número de ensayos, ilustrando la ley de los grandes números.
Función de Masa de Probabilidad (PMF)
La Función de Masa de Probabilidad (PMF) es una función que describe la probabilidad de que una variable aleatoria discreta tome un valor específico. Es una función que devuelve la probabilidad de que una variable aleatoria discreta sea exactamente igual a algún valor. Es una función que asocia a cada punto de su espacio muestral X la probabilidad de que esta lo asuma. La función de probabilidad suele ser el medio principal para definir una distribución de probabilidad discreta, y tales funciones existen para variables aleatorias escalares o multivariantes, cuyo dominio es discreto.
La función de masa de probabilidad de un dado. Todos los números tienen la misma probabilidad de aparecer cuando este es tirado.
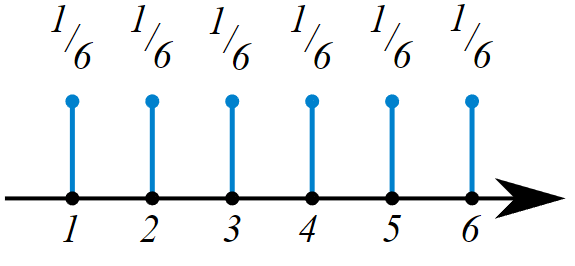
Por ejemplo, supongamos que lanzamos una moneda justa varias veces y contamos el número de caras. La función de masa de probabilidad que describe la probabilidad de cada resultado posible (p. ej., 0 caras, 1 cara, 2 caras, etc.) se denomina distribución binomial. Los parámetros para la distribución binomial son:
npara el número de intentos (por ejemplo,n=10si lanzamos una moneda 10 veces)ppara la probabilidad de éxito en cada prueba (probabilidad de observar un resultado particular en cada prueba. En este ejemplo,p= 0,5porque la probabilidad de observar caras en un lanzamiento de moneda justo es 0,5)
Si lanzamos una moneda normal 10 veces, decimos que el número de caras observadas sigue una distribución Binomial(n=10, p=0.5). El siguiente gráfico muestra la función de masa de probabilidad para este experimento. Las alturas de las barras representan la probabilidad de observar cada resultado posible calculado por el PMF.
Veamos cómo cambia la forma de la distribución binomial a medida que cambia el tamaño de la muestra.
Utilice el control deslizante para cambiar el valor de x lanzamientos de moneda justos, entre uno y diez. Las alturas de las barras resultantes representan la probabilidad de observar diferentes valores de caras en x número de lanzamientos de moneda justos. Puede pasar el cursor sobre cada barra y ver el valor numérico real de la altura de la barra. Las barras más altas representan resultados más probables.
Observe que a medida que x aumenta, las barras se hacen más pequeñas. Esto se debe a que la suma de las alturas de todas las barras siempre será igual a 1. Entonces, cuando x es mayor, el número de caras que podemos observar aumenta y la probabilidad debe dividirse entre más valores.
Binomial Distribution: Calculating Probability of a Given Number of Heads
Calcular probabilidades usando Python
El método binom.pmf() de la biblioteca scipy.stats se puede utilizar para calcular el PMF de la distribución binomial en cualquier valor. Este método toma 3 valores:
x: el valor del interésn: el número de ensayosp: la probabilidad de éxito
Por ejemplo, supongamos que lanzamos una moneda normal 10 veces y contamos el número de caras. Podemos usar la función binom.pmf() para calcular la probabilidad de observar 6 cabezas de la siguiente manera:
# import necessary library
import scipy.stats as stats
# st.binom.pmf(x, n, p)
print(stats.binom.pmf(6, 10, 0.5))
Output
0.205078
Observe que dos de los tres valores que entran en el método stats.binomial.pmf() son los parámetros que definen la distribución binomial: n representa el número de intentos y p representa la probabilidad de éxito.
Uso de la función de masa de probabilidad en un rango
Hemos visto que podemos calcular la probabilidad de observar un valor específico usando una función de masa de probabilidad. ¿Qué pasa si queremos encontrar la probabilidad de observar un rango de valores para una variable aleatoria discreta? Una forma de hacer esto es sumando la probabilidad de cada valor.
Por ejemplo, digamos que lanzamos una moneda justa 5 veces y queremos saber la probabilidad de obtener entre 1 y 3 caras. Podemos visualizar este escenario con la función de masa de probabilidad:

Podemos calcular esto usando la siguiente ecuación donde P(x) es la probabilidad de observar el número x de éxitos (cara en este caso):
P(1 to 3 heads) = P(1<= X <=3)
P(1 to 3 heads) = P(X=1) + P(X=2) + P(X=3)
P(1 to 3 heads) = 0.1562 + 0.3125 + 0.3125
P(1 to 3 heads) = 0.7812
Visualicemos lo que significa tomar la probabilidad de un rango. Utilice los controles deslizantes para seleccionar un rango de valores que representen el número de caras que podríamos observar en 10 lanzamientos de moneda justos.
Pruebe diferentes rangos para ver cómo cambian las probabilidades para diferentes valores. Pase el cursor sobre una barra individual para ver la altura de la barra (que corresponde a la probabilidad de que ocurra el valor).
Binomial Distribution: Calculating Probability of a Range
Función de masa de probabilidad en un rango usando Python
Podemos utilizar el mismo método binom.pmf() de la biblioteca scipy.stats para calcular la probabilidad de observar un rango de valores. Como se mencionó en un ejercicio anterior, el método binom.pmf toma 3 valores:
x: el valor del interésn: el número de ensayosp: la probabilidad de éxito
Por ejemplo, podemos calcular la probabilidad de observar entre 2 y 4 caras en 10 lanzamientos de moneda de la siguiente manera:
import scipy.stats as stats
# calculating P(2-4 heads) = P(2 heads) + P(3 heads) + P(4 heads) for flipping a coin 10 times
print(stats.binom.pmf(2, n=10, p=.5)
+ stats.binom.pmf(3, n=10, p=.5)
+ stats.binom.pmf(4, n=10, p=.5))
Output:
0.366211
También podemos calcular la probabilidad de observar menos de un cierto valor, digamos 3 caras, sumando las probabilidades de los valores debajo de él:
import scipy.stats as stats
# calculating P(less than 3 heads) = P(0 heads) + P(1 head) + P(2 heads) for flipping a coin 10 times
print(stats.binom.pmf(0, n=10, p=.5)
+ stats.binom.pmf(1, n=10, p=.5)
+ stats.binom.pmf(2, n=10, p=.5))
Output
0.0546875
Tenga en cuenta que debido a que nuestro rango deseado es inferior a 3 cabezas, no incluimos ese valor en la suma.
Cuando hay muchos valores de interés posibles, esta tarea de sumar probabilidades puede resultar difícil. Si queremos saber la probabilidad de observar 8 o menos caras en 10 lanzamientos de moneda, debemos sumar los valores del 0 al 8:
import scipy.stats as stats
var = stats.binom.pmf(0, n = 10, p = 0.5)
+ stats.binom.pmf(1, n = 10, p = 0.5)
+ stats.binom.pmf(2, n = 10, p = 0.5)
+ stats.binom.pmf(3, n = 10, p = 0.5)
+ stats.binom.pmf(4, n = 10, p = 0.5)
+ stats.binom.pmf(5, n = 10, p = 0.5)
+ stats.binom.pmf(6, n = 10, p = 0.5)
+ stats.binom.pmf(7, n = 10, p = 0.5)
+ stats.binom.pmf(8, n = 10, p = 0.5)
Output
0.98926
Esto implica una gran cantidad de código repetitivo. En su lugar, también podemos utilizar el hecho de que la suma de las probabilidades de todos los valores posibles es igual a 1:
P(0to8heads) + P(9to10heads) = P(0to10heads) = 1
P(0to8heads) = 1 − P(9to10heads)
Ahora, en lugar de sumar 9 valores para las probabilidades entre 0 y 8 caras, podemos hacer 1 menos la suma de dos valores y obtener el mismo resultado:
import scipy.stats as stats
# less than or equal to 8
1 - (stats.binom.pmf(9, n=10, p=.5) + stats.binom.pmf(10, n=10, p=.5))
Output
0.98926
Función de distribución acumulativa
La función de distribución acumulativa para una variable aleatoria discreta se puede derivar de la función de masa de probabilidad. Sin embargo, en lugar de la probabilidad de observar un valor específico, la función de distribución acumulativa proporciona la probabilidad de observar un valor específico O MENOS.
Como se analizó anteriormente, las probabilidades de todos los valores posibles en una distribución de probabilidad dada suman 1. El valor de una función de distribución acumulativa en un valor dado es igual a la suma de las probabilidades menores que él, con un valor de 1 para la mayor número posible.
CDF de Ejemplo para Diferentes Distribuciones
- Distribución Discreta: Si una variable aleatoria \(𝑋\) es discreta, la CDF tiene saltos en los puntos donde la variable tiene una probabilidad distinta de cero.
- Distribución Continua: Si una variable aleatoria \(𝑋\) es continua, la CDF es una función continua. Ejemplo: para una distribución normal con media \(𝜇\) y desviación estándar \(𝜎\), la CDF se representa usando la función de error, la cual es una integral de la función de densidad de probabilidad (PDF).
Mostramos cómo se puede utilizar la función de masa de probabilidad para calcular la probabilidad de observar menos de 3 caras en 10 lanzamientos de moneda sumando las probabilidades de observar 0, 1 y 2 caras. La función de distribución acumulativa produce la misma respuesta al evaluar la función en CDF(X=2). En este caso, utilizar el CDF es más sencillo que el PMF porque requiere un cálculo en lugar de tres.
La animación del enlace muestra la relación entre la función de masa de probabilidad y la función de distribución acumulativa. El gráfico superior es el PMF, mientras que el gráfico inferior es el CDF correspondiente. Al observar la gráfica de una CDF, cada valor del eje y es la suma de las probabilidades menores o iguales que él en la PMF.
Podemos usar una función de distribución acumulativa para calcular la probabilidad de un rango específico tomando la diferencia entre dos valores de la función de distribución acumulativa. Por ejemplo, para encontrar la probabilidad de observar entre 3 y 6 caras, podemos tomar la probabilidad de observar 6 o menos cabezas y restar la probabilidad de observar 2 o menos caras. Esto deja un remanente de entre 3 y 6 cabezas.
La imagen de la derecha demuestra cómo funciona esto. Es importante tener en cuenta que para incluir el límite inferior en el rango, el valor que se resta debe ser uno menos que el límite inferior. En este ejemplo, queríamos saber la probabilidad de 3 a 6, que incluye 3.
Usando la función de distribución acumulativa en Python
Podemos utilizar el método binom.cdf() de la biblioteca scipy.stats para calcular la función de distribución acumulativa. Este método toma 3 valores:
x: el valor de interés, buscando la probabilidad de este valor o menosn: el tamaño de la muestrap: la probabilidad de éxito
Calcular matemáticamente la probabilidad de observar 6 o menos caras en 10 lanzamientos de moneda justos (0 a 6 caras) se parece a lo siguiente:
P(6 or fewer heads) = P(0 to 6 heads)
El codigo en Python es:
import scipy.stats as stats
print(stats.binom.cdf(6, 10, 0.5))
Output
0.828125
Se puede pensar que calcular la probabilidad de observar entre 4 y 8 caras en 10 lanzamientos de moneda justos es tomar la diferencia del valor de la función de distribución acumulativa en 8 de la función de distribución acumulativa en 3:
P(4 to 8 Heads) = P(0 to 8 Heads) − P(0 to 3 Heads)
En Python utilizamos el codigo:
import scipy.stats as stats
print(stats.binom.cdf(8, 10, 0.5) - stats.binom.cdf(3, 10, 0.5))
Output
0.81738
Para calcular la probabilidad de observar más de 6 caras en 10 lanzamientos de moneda justos, restamos el valor de la función de distribución acumulativa en 6 de 1. Matemáticamente, esto se parece a lo siguiente:
P(more than 6 Heads) = 1 - P(6 or fewer Heads)
Tenga en cuenta que “más de 6 cabezas” no incluye 6. En Python, calcularíamos esta probabilidad usando el siguiente código:
import scipy.stats as stats
print(1 - stats.binom.cdf(6, 10, 0.5))
Output
0.171875
Tipos de Variables Aleatorias Discretas
Los tipos de variables aleatorias discretas se clasifican comúnmente según las distribuciones de probabilidad que describen cómo se comportan los datos asociados a estas variables. Aquí describo algunas de las distribuciones más comunes y utilizadas para variables aleatorias discretas. En Python, la librería scipy.stats proporciona implementaciones de las PMFs para muchas distribuciones discretas comunes, lo que facilita su cálculo en la práctica. Estas funciones son extremadamente útiles para simulaciones, modelado estadístico y análisis probabilístico en una amplia gama de aplicaciones.
-
Distribución Binomial:
Usada cuando se están observando el número de éxitos en un número fijo de ensayos independientes y cada ensayo tiene solo dos posibles resultados (éxito o fracaso).
La PMF de una distribución binomial describe la probabilidad de obtener un número específico de éxitos en un número fijo de ensayos independientes, cada uno con dos posibles resultados y una misma probabilidad de éxito.from scipy.stats import binom import numpy # Parámetros n = 10 # número de ensayos p = 0.5 # probabilidad de éxito size = 100 # muestras a generar # Generar Variables numpy.random.binomial(n, p, size) # Calcular PMF para un valor específico k = 5 # número de éxitos prob = binom.pmf(k, n, p) print(f"Probabilidad de {k} éxitos en {n} ensayos: {prob:.4f}") -
Distribución de Poisson: Aplica para modelar el número de eventos en un intervalo de tiempo o espacio fijo cuando estos eventos ocurren con una tasa media conocida y de manera independiente entre sí. La PMF de una distribución de Poisson mide la probabilidad de un número determinado de eventos ocurriendo en un intervalo fijo, dado que estos eventos ocurren con una tasa media conocida y de manera independiente.
from scipy.stats import poisson import numpy lambda_ = 3 # tasa media de eventos por intervalo zize = 10 # número de muestras a generar. # Generar variables numpy.random.poisson(lambda_, size) # Calcular PMF k = 4 # número de eventos prob = poisson.pmf(k, lambda_) print(f"Probabilidad de {k} eventos: {prob:.4f}") -
Distribución Geométrica: Describe el número de ensayos necesarios para obtener el primer éxito en una secuencia de ensayos independientes, cada uno con dos posibles resultados. La PMF de una distribución geométrica describe la probabilidad de que el primer éxito ocurra en el ensayo \(𝑘\)
from scipy.stats import geom import numpy p = 0.2 # probabilidad de éxito en cada ensayo zize = 10 # número de muestras a generar. # generar variable numpy.random.geometric(p, size) # Calcular PMF k = 5 # ensayo en el que ocurre el primer éxito prob = geom.pmf(k, p) print(f"Probabilidad de primer éxito en el intento {k}: {prob:.4f}") -
Distribución Binomial Negativa: Generaliza la distribución geométrica para contar el número de ensayos requeridos para obtener un número fijo de éxitos. Esta distribución cuenta cuántos ensayos son necesarios para lograr un número especificado de éxitos.
from scipy.stats import nbinom import numpy r = 5 # número de éxitos deseados p = 0.5 # probabilidad de éxito en cada ensayo zize = 10 # número de muestras a generar. # generar variable numpy.random.negative_binomial(n, p, size) # Calcular PMF k = 10 # total de ensayos prob = nbinom.pmf(k-r, r, p) print(f"Probabilidad de alcanzar {r} éxitos en {k} ensayos: {prob:.4f}") -
Distribución Hipergeométrica: Modela el número de éxitos en una muestra de tamaño fijo tomada sin reemplazo de una población que consta de dos tipos de objetos (éxitos y fracasos).
La PMF de la distribución hipergeométrica describe la probabilidad de obtener un número determinado de éxitos en una muestra extraída sin reemplazo de una población finita que consta de dos tipos de objetos.from scipy.stats import hypergeom import numpy M = 20 # tamaño total de la población n = 7 # número de éxitos en la población N = 12 # tamaño de la muestra # Calcular PMF k = 3 # número de éxitos observados en la muestra prob = hypergeom.pmf(k, M, n, N) print(f"Probabilidad de {k} éxitos en una muestra de {N}: {prob:.4f}") # generar variable ngood # número de elementos "buenos" en la población. nbad # número de elementos "malos" en la población. nsample # número de elementos a muestrear (sin reemplazo). size # número de muestras a generar. numpy.random.hypergeometric(ngood, nbad, nsample, size=None) - Distribución Uniforme Discreta:
- Todos los valores posibles de la variable tienen la misma probabilidad de ocurrir.
- Parámetros: el mínimo y máximo valor que puede tomar la variable.
- Distribución de Bernoulli:
- Un caso especial de la distribución binomial con un solo ensayo \(n = 1\).
- Parámetro: probabilidad de éxito \(p\).
- Distribución Multinomial:
- Extensión de la distribución binomial para situaciones en las que cada ensayo puede resultar en más de dos categorías.
- Parámetros: número de ensayos \(n\) y vector de probabilidades \(p\) para cada categoría.
Estas distribuciones permiten modelar una gran variedad de procesos y fenómenos en diversos campos como la biología, ingeniería, economía, ciencias sociales, y más. Cada tipo de distribución proporciona un modelo estadístico que se adapta a las características específicas de los datos y la naturaleza del experimento o la observación realizada.
Variables aleatorias continuas
Las variables aleatorias continuas son aquellas que pueden tomar cualquier valor numérico dentro de un intervalo o conjunto de intervalos, a diferencia de las variables aleatorias discretas que tienen valores contables y separados. Este tipo de variables es fundamental en estadística y probabilidad para modelar fenómenos que requieren una escala de medida infinita y continua.
Características Principales
- Valores no Contables: Las variables aleatorias continuas pueden adoptar cualquier valor dentro de un rango específico, que puede ser finito o infinito.
- Función de Densidad de Probabilidad (PDF): A diferencia de las variables discretas que usan una función de probabilidad de masa, las continuas se describen mediante una función de densidad de probabilidad. Esta función no proporciona probabilidades directamente, sino que el área bajo la curva de la función entre dos puntos corresponde a la probabilidad de que la variable aleatoria caiga dentro de ese intervalo.
Ejemplos de Variables Aleatorias Continuas
- Altura de los estudiantes en una clase: La altura puede variar continuamente y puede ser cualquier valor dentro de un rango razonable, por ejemplo, entre 1.50 metros y 2.00 metros.
- Tiempo necesario para completar una tarea: Este tiempo puede ser cualquier número no negativo, medido con precisión hasta fracciones de segundo.
- Presión en un tanque de gas: La presión puede fluctuar y tomar cualquier valor dentro de los límites de seguridad del tanque.
Funcion de densidad de probabilidad
De manera similar a cómo las variables aleatorias discretas se relacionan con las funciones de masa de probabilidad, las variables aleatorias continuas se relacionan con las funciones de densidad de probabilidad. Definen las distribuciones de probabilidad de variables aleatorias continuas y abarcan todos los valores posibles que puede adoptar la variable aleatoria dada.
Cuando se representa gráficamente, una función de densidad de probabilidad es una curva que atraviesa todos los valores posibles que puede tomar la variable aleatoria, y el área total bajo esta curva suma 1.
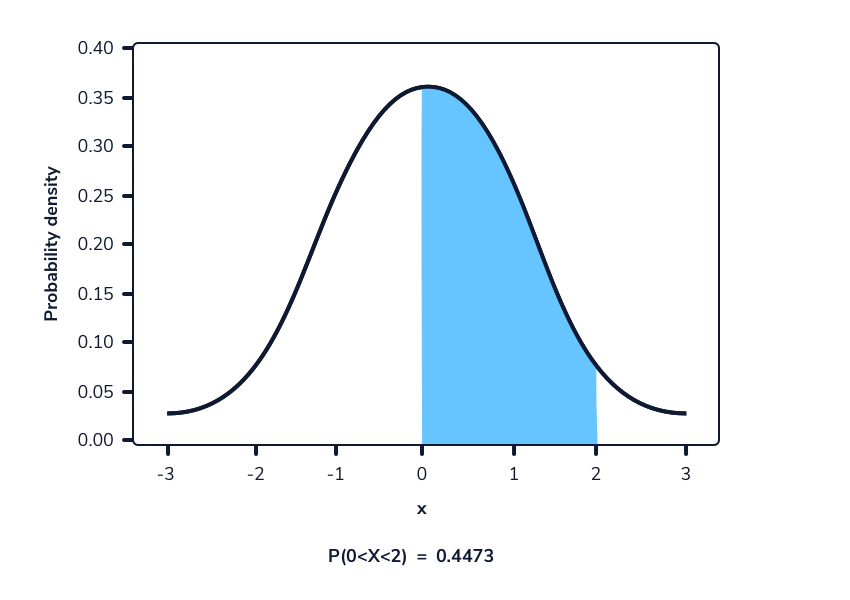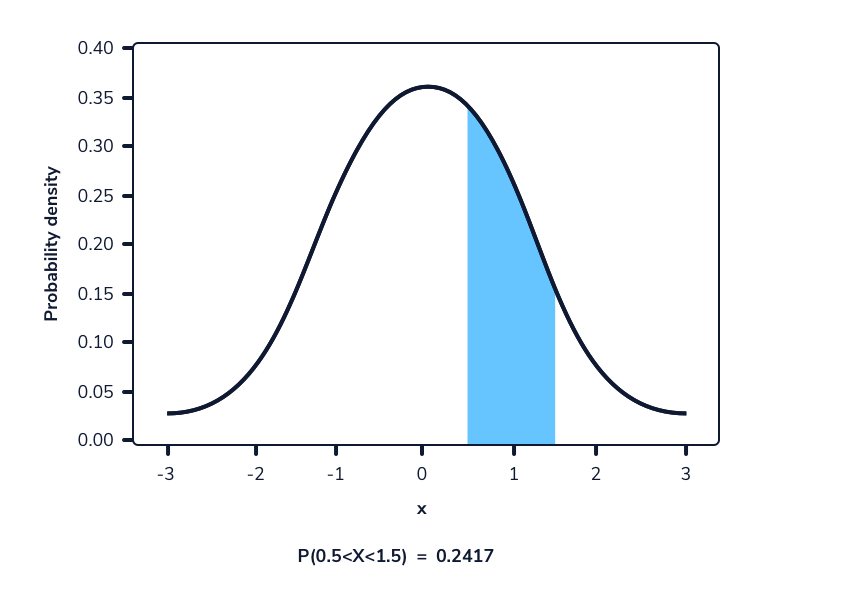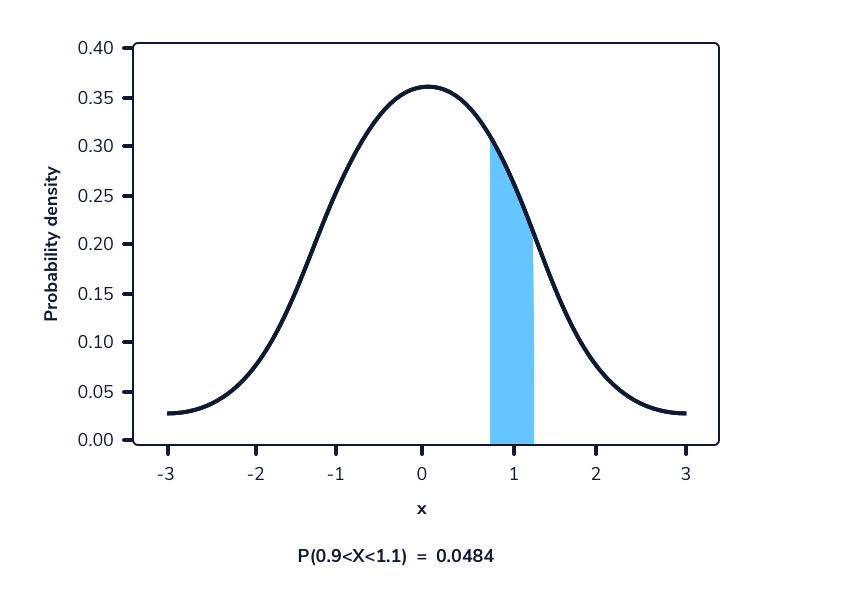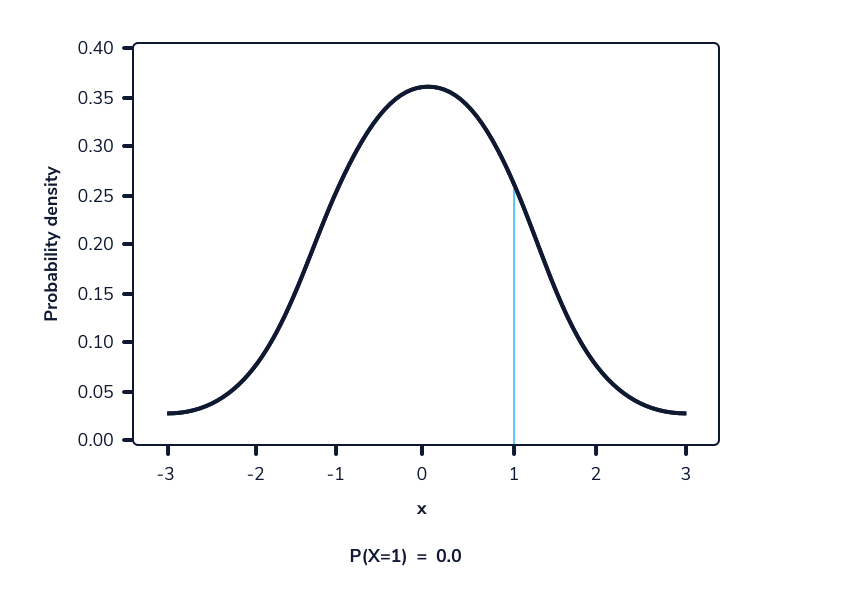
La siguiente imagen muestra una función de densidad de probabilidad. El área resaltada representa la probabilidad de observar un valor dentro del rango resaltado.
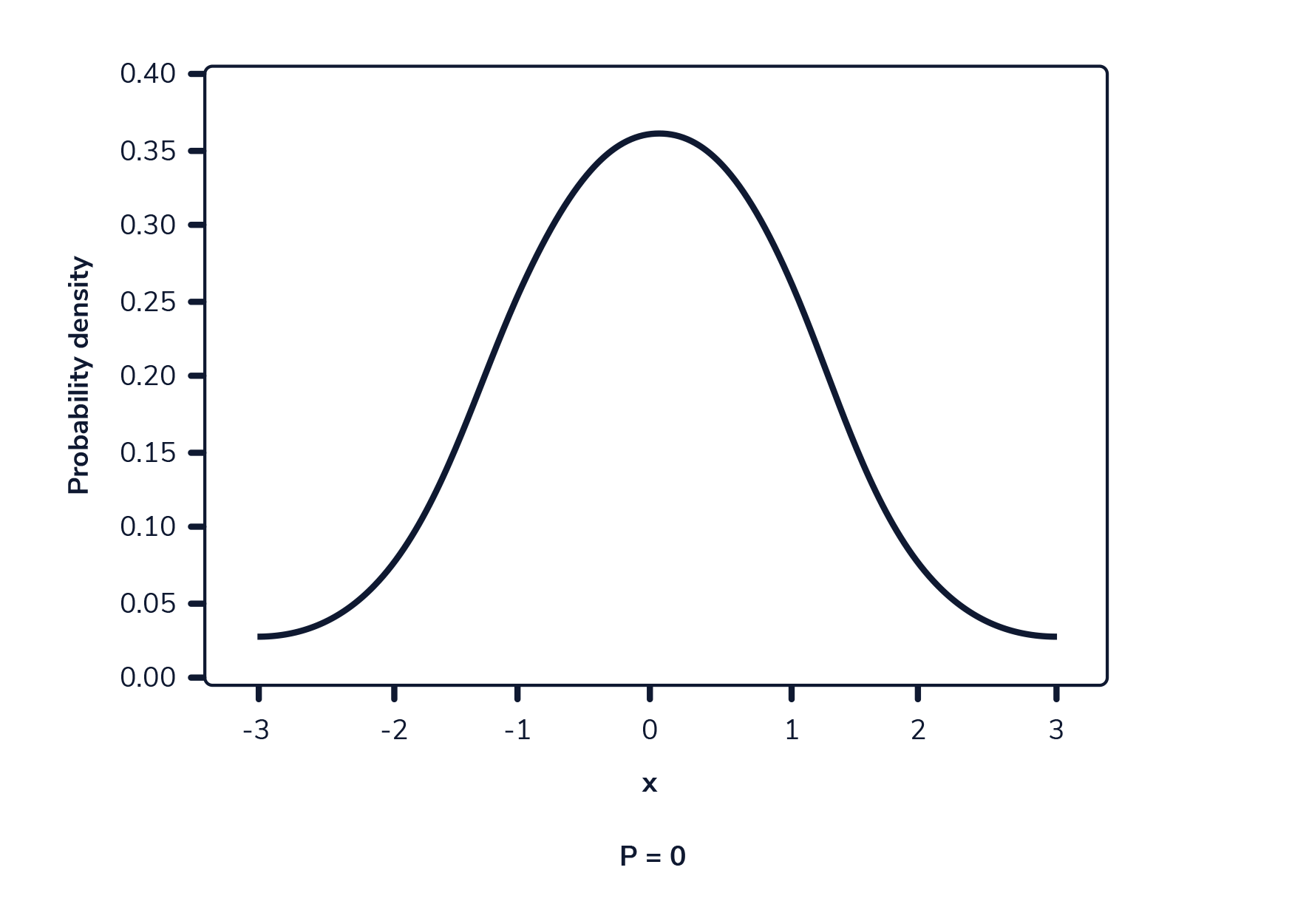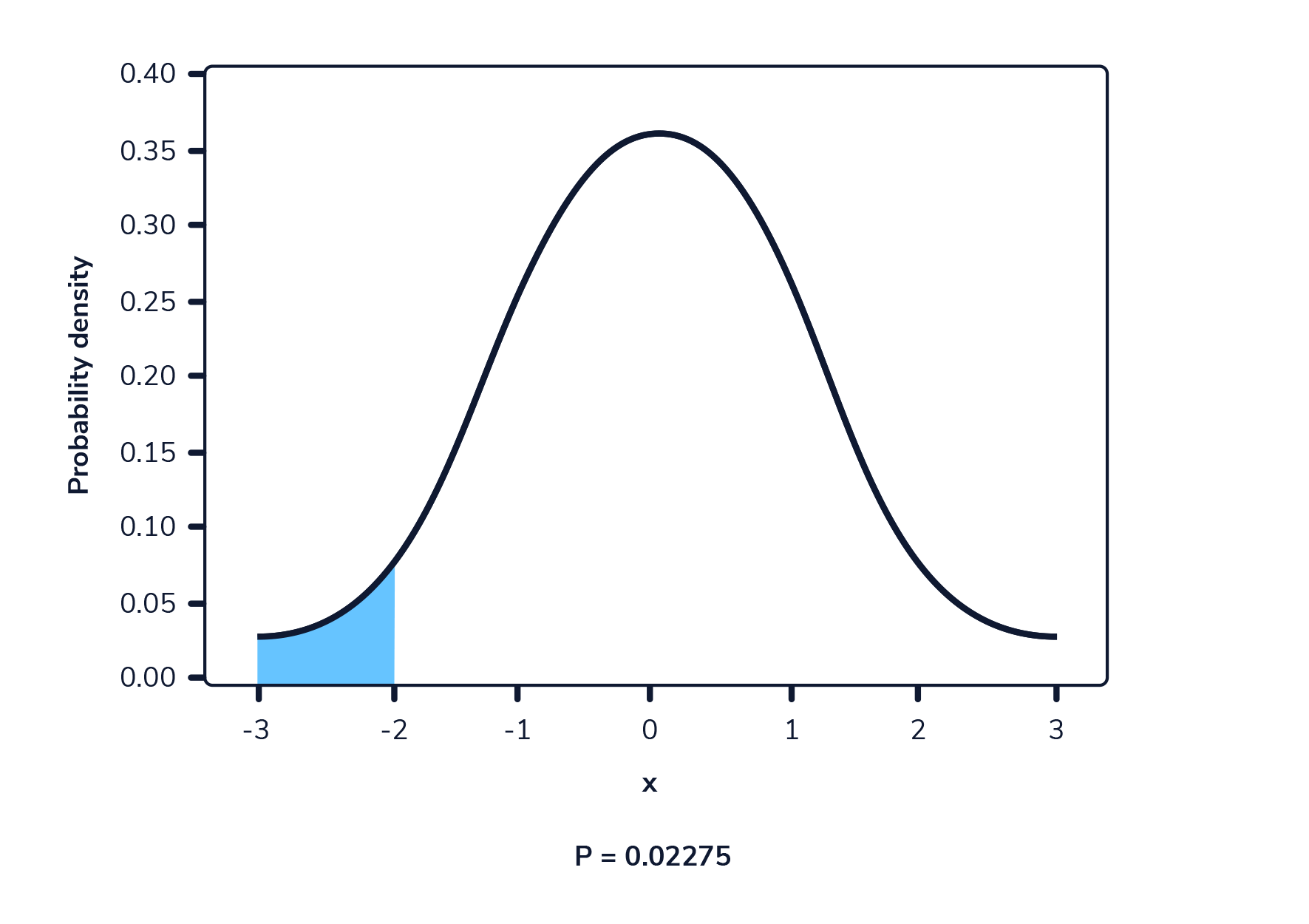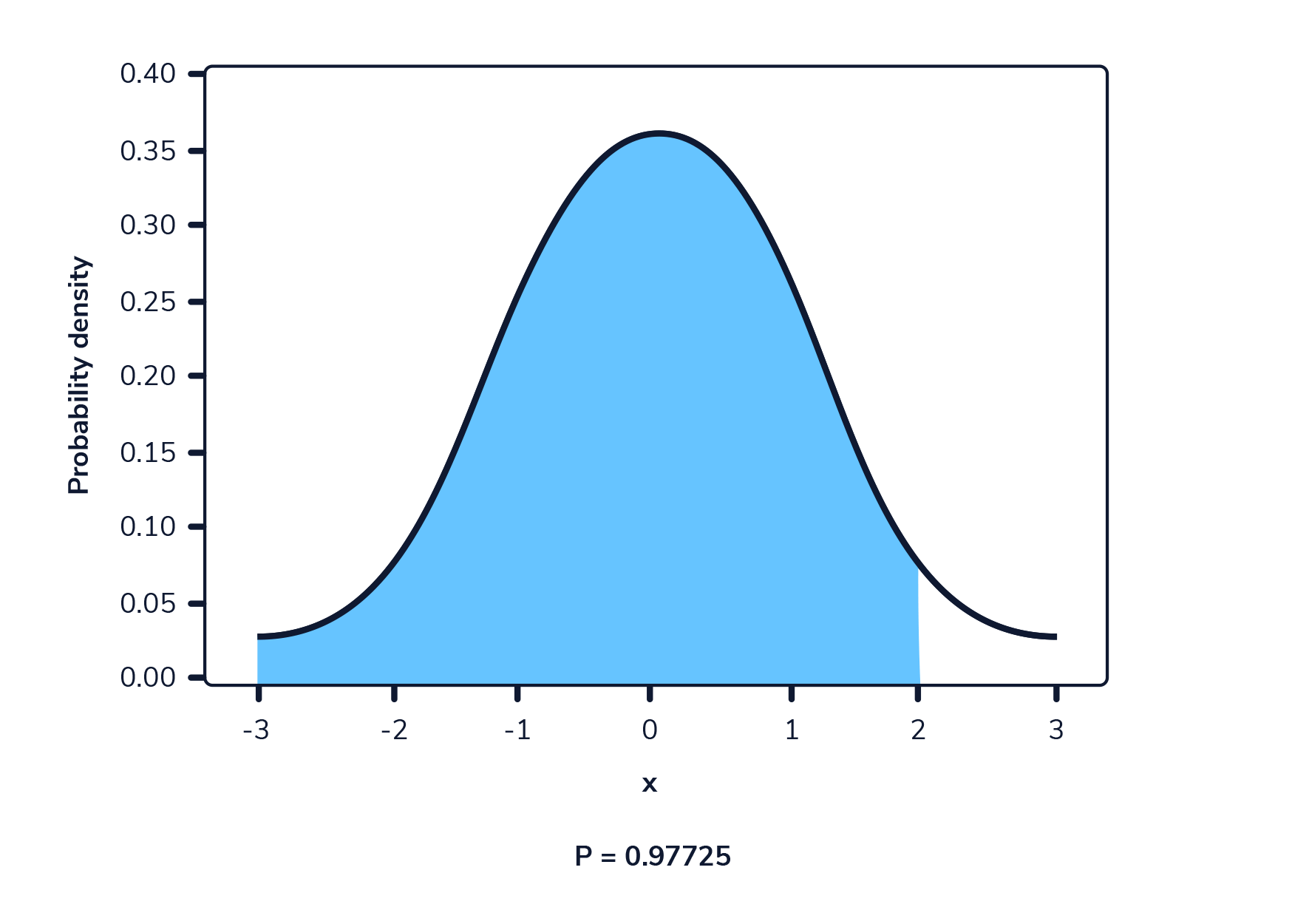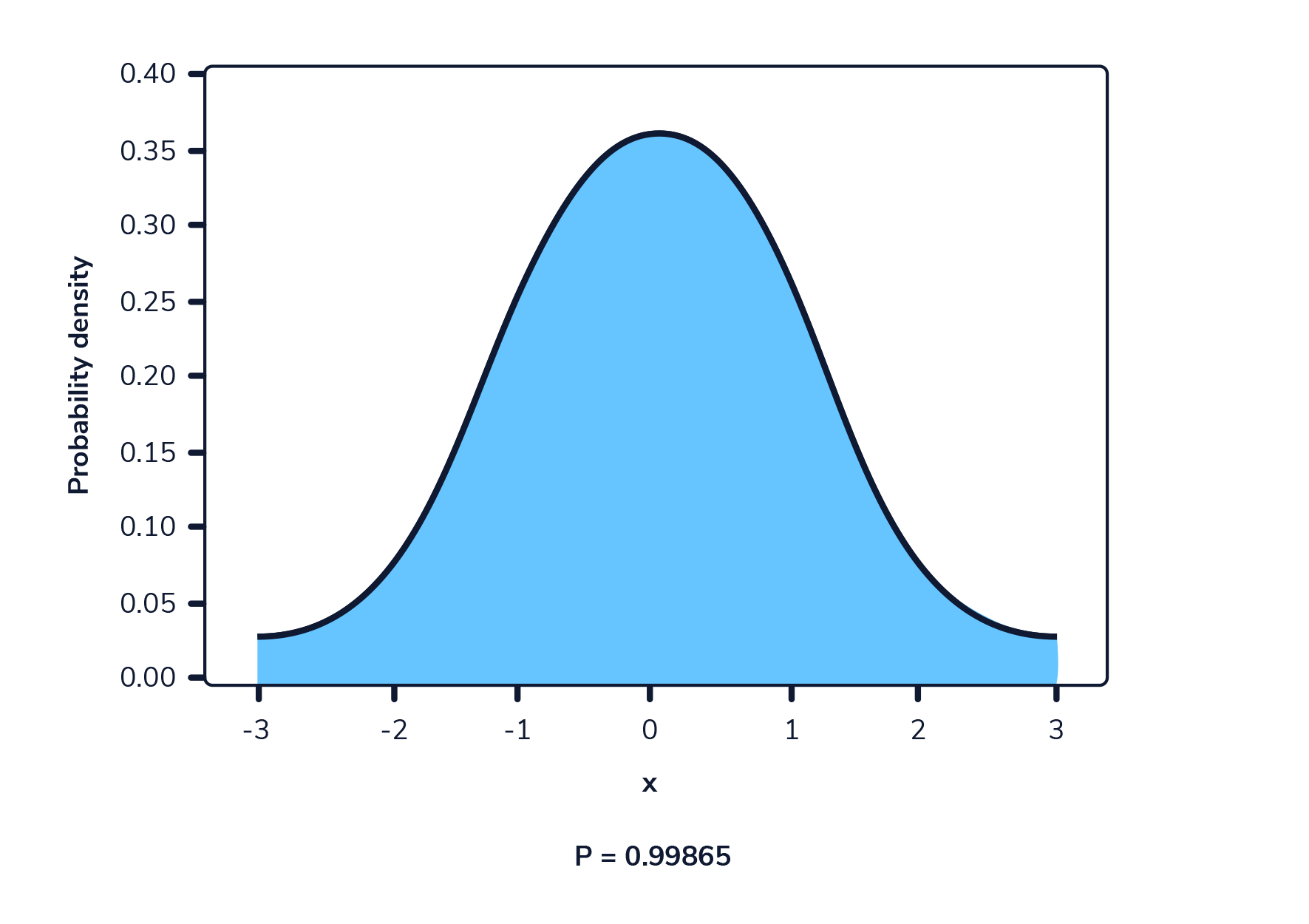
En una función de densidad de probabilidad, no podemos calcular la probabilidad en un solo punto. Esto se debe a que el área de la curva debajo de un único punto es siempre cero. El siguiente gif muestra esto.
Como podemos ver en la imagen anterior, a medida que el intervalo se hace más pequeño, el ancho del área bajo la curva también se hace más pequeño. Al intentar evaluar el área bajo la curva en un punto específico, el ancho de esa área se vuelve 0 y, por lo tanto, la probabilidad es igual a 0.
Podemos calcular el área bajo la curva usando la función de distribución acumulativa para la distribución de probabilidad dada.
Por ejemplo, las alturas caen bajo un tipo de distribución de probabilidad llamada distribución normal. Los parámetros de la distribución normal son la media y la desviación estándar, y utilizamos la forma Normal(media, desviación estándar) como abreviatura.
Sabemos que la altura de las mujeres tiene una media de 167,64 cm con una desviación estándar de 8 cm, lo que las sitúa bajo la distribución Normal(167,64,8).
Digamos que queremos saber la probabilidad de que una mujer elegida al azar mida menos de 158 cm. Podemos usar la función de distribución acumulativa para calcular el área bajo la curva de la función de densidad de probabilidad de 0 a 158 para encontrar esa probabilidad.
Podemos calcular el área de la región azul en Python usando el método norm.cdf() de la biblioteca scipy.stats. Este método toma 3 valores:
x: el valor del interésloc:la media de la distribución de probabilidadscale: la desviación estándar de la distribución de probabilidad
import scipy.stats as stats
# stats.norm.cdf(x, loc, scale)
print(stats.norm.cdf(158, 167.64, 8))
Output
0.1141
Funciones de densidad de probabilidad y función de distribución acumulativa
Podemos tomar la diferencia entre dos rangos superpuestos para calcular la probabilidad de que una selección aleatoria esté dentro de un rango de valores para distribuciones continuas. Este es esencialmente el mismo proceso que calcular la probabilidad de un rango de valores para distribuciones discretas.
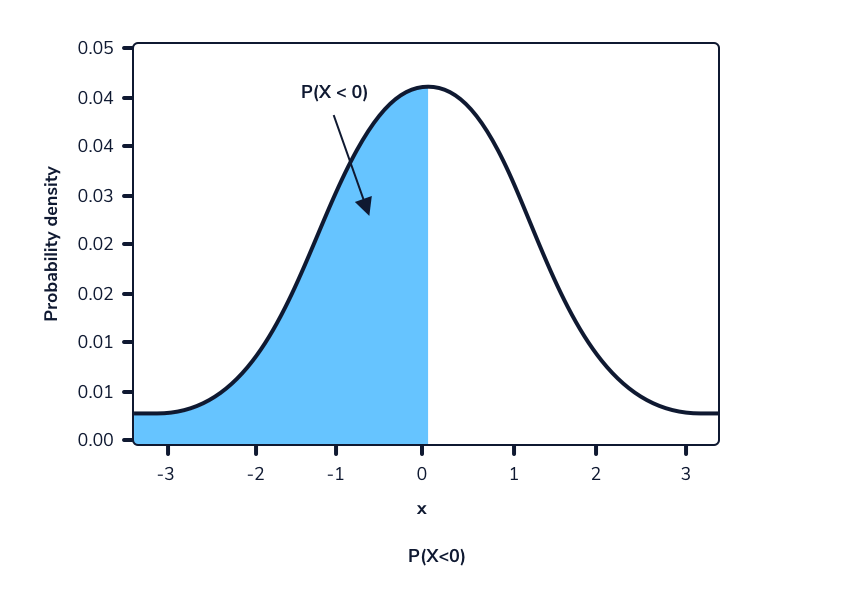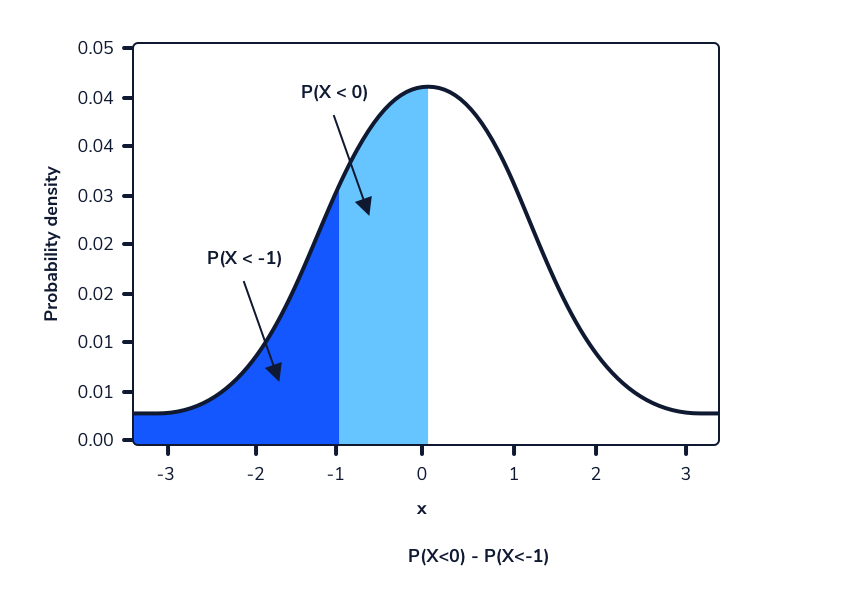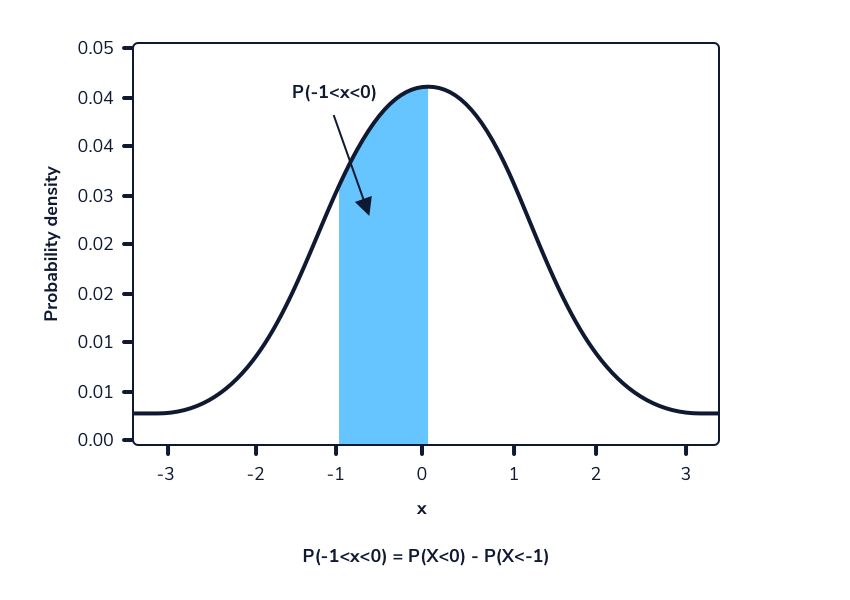
Digamos que queremos calcular la probabilidad de observar aleatoriamente a una mujer de entre 165 cm y 175 cm, suponiendo que las alturas todavía siguen la distribución Normal (167,74, 8). Podemos calcular la probabilidad de observar estos valores o menos. La diferencia entre estas dos probabilidades será la probabilidad de observar aleatoriamente a una mujer en este rango dado. Esto se puede hacer en Python usando el método norm.cdf() de la biblioteca scipy.stats. Como se mencionó anteriormente, este método adopta 3 valores:
import scipy.stats as stats
# P(165 < X < 175) = P(X < 175) - P(X < 165)
# stats.norm.cdf(x, loc, scale) - stats.norm.cdf(x, loc, scale)
print(stats.norm.cdf(175, 167.74, 8) - stats.norm.cdf(165, 167.74, 8))
Output
0.45194
También podemos calcular la probabilidad de observar aleatoriamente un valor o mayor restando de 1 la probabilidad de observar menos que el valor dado. Esto es posible porque sabemos que el área total bajo la curva es 1, por lo que la probabilidad de observar algo mayor que un valor es 1 menos la probabilidad de observar algo menor que el valor dado.
Digamos que queremos calcular la probabilidad de observar a una mujer que mide más de 172 centímetros, suponiendo que las alturas todavía siguen la distribución Normal (167,74, 8). Podemos pensar en esto como lo opuesto a observar a una mujer que mide menos de 172 centímetros. Podemos visualizarlo de esta manera:
Podemos usar el siguiente código para calcular el área azul tomando 1 menos el área roja:
import scipy.stats as stats
# P(X > 172) = 1 - P(X < 172)
# 1 - stats.norm.cdf(x, loc, scale)
print(1 - stats.norm.cdf(172, 167.74, 8))
Output
0.45194
Tipos de Variables Aleatorias Continuas
-
Normal (Gaussiana):
loc: media de la distribución (mu).scale: desviación estándar de la distribución (sigma).size: número de muestras a generar.
numpy.random.normal(loc=0.0, scale=1.0, size=None)Genera números a partir de una distribución normal con media
locy desviación estándarscale. -
Exponencial:
scale: inverso de la tasa (lambda), a veces llamado parámetro de escala.size: número de muestras a generar.
numpy.random.exponential(scale=1.0, size=None)Genera números a partir de una distribución exponencial con un parámetro de escala.
-
Uniforme:
low: límite inferior del rango de los valores.high: límite superior del rango de los valores.size: número de muestras a generar.
numpy.random.uniform(low=0.0, high=1.0, size=None)Genera números a partir de una distribución uniforme entre
lowyhigh. -
Beta:
a: parámetro de forma alpha.b: parámetro de forma beta.size: número de muestras a generar.
numpy.random.beta(a, b, size=None)Genera números a partir de una distribución beta con parámetros
ayb. -
Gamma:
shape: parámetro de forma (k).scale: parámetro de escala (theta).size: número de muestras a generar.
numpy.random.gamma(shape, scale=1.0, size=None)Genera números a partir de una distribución gamma con un parámetro de forma y escala.
Estos métodos permiten simular datos que siguen estas distribuciones, lo que es útil en simulaciones, pruebas de hipótesis, y para entender mejor el comportamiento estadístico de fenómenos modelados por estas distribuciones.

