Summary Statistics

En el mundo del análisis de datos, trabajar con datos tabulares es una práctica común. Al analizar datos tabulares, a veces necesitamos obtener información rápida sobre los patrones y la distribución de los datos. Estos rápidos conocimientos suelen proporcionar la base para exploraciones y análisis adicionales. Nos referimos a estos conocimientos rápidos como estadísticas resumidas. Las estadísticas resumidas son muy útiles enproyectos de análisis de datos exploratorios porque nos ayudan a realizar una inspección rápida de los datos que estamos analizando.

Analisis Univariado

Los resúmenes univariados se centran en la descripción y análisis de una sola variable a la vez. Este tipo de análisis es fundamental en estadística y análisis de datos, ya que proporciona una comprensión básica de las características y la distribución de los datos en una dimensión. Los resúmenes univariados son un paso inicial crucial en el análisis exploratorio de datos (EDA) para identificar patrones, tendencias, anomalías y posibles relaciones entre variables. A continuación, se detallan algunos de los conceptos y técnicas más importantes en los resúmenes univariados:

Resumenes de Variables Cuantitativas

Medidas de Tendencia Central

La medida de tendencia central tiende a describir el valor promedio o medio de conjuntos de datos que se supone proporciona un resumen óptimo de todo el conjunto de mediciones. Este valor es un número que de alguna manera es central para el conjunto. Las medidas más comunes para analizar la frecuencia de distribución de los datos son la media, la mediana y la moda.

Media (Promedio):
Es la suma de todos los valores de la variable dividida por el número de observaciones. Proporciona el centro de gravedad de la distribución, pero es sensible a valores extremos (outliers).

# Pandas
mean = df['column'].mean()
# Numpy
mean = np.mean(df['column'])

Mediana:
Es el valor que divide al conjunto de datos en dos partes iguales cuando los datos están ordenados. La mediana es menos sensible a valores extremos y proporciona una mejor medida del centro para distribuciones sesgadas.

# Pandas
median = df['column'].median()
# Numpy
median = np.median(df['column'])

Media recortada:
Es una medida estadística de tendencia central que se asemeja a la media aritmética, pero con una diferencia clave: antes de calcular la media, se eliminan los valores extremos de ambos extremos de un conjunto de datos. El porcentaje exacto de datos a recortar depende del análisis, pero un enfoque común es eliminar el 5% de los valores más bajos y el 5% de los valores más altos.

from scipy.stats import trim_mean
print(f'Media Recortada: Rs.{round(trim_mean(df.column, proportiontocut=0.1), 2)}')

Moda:
Es el valor o valores que aparecen con mayor frecuencia en el conjunto de datos. Es útil para datos categóricos y para identificar picos en distribuciones multimodales.

# Pandas
mode = df['column'].mode()
# Stats
from scipy import stats
node = stats.mode(df['column'])

Medidas de Dispersión

El segundo tipo de estadística descriptiva es la medida de dispersión , también conocida como medida de variabilidad . Se utiliza para describir la variabilidad en un conjunto de datos, que puede ser una muestra o una población. Generalmente se utiliza junto con una medida de tendencia central para proporcionar una descripción general de un conjunto de datos. Una medida de dispersión/variabilidad/extensión nos da una idea de qué tan bien representa la tendencia central los datos. Si analizamos el conjunto de datos de cerca, a veces, la media/promedio puede no ser la mejor representación de los datos porque variará cuando haya grandes variaciones entre los datos. En tal caso, una medida de dispersión representará la variabilidad en un conjunto de datos con mucha más precisión.

Múltiples técnicas proporcionan medidas de dispersión en nuestro conjunto de datos. Algunos métodos comúnmente utilizados son la desviación estándar (o varianza), los valores mínimo y máximo de las variables, el rango, la curtosis y la asimetría

Rango: Es la diferencia entre el valor máximo y mínimo de la variable. Proporciona una idea de la amplitud de la distribución.

# Pandas
max = df['column'].max()
min = df['column'].min()
# Numpy
max = np.max(df['column'])
min = np.min(df['column'])
# Para calcular el rango
range = max - min

Varianza:
Estas medidas indican cuánto tienden a dispersarse los valores alrededor de la media. La varianza es el promedio de las diferencias al cuadrado de la media, y la desviación estándar es la raíz cuadrada de la varianza.

# Pandas
median = df['column'].var()
# Numpy
median = np.var(df['column'])

Desviación Estándar
La desviación estándar esse deriva de la varianza y es simplemente la raíz cuadrada de la varianza. La desviación estándar suele ser más intuitiva porque se expresa en las mismas unidades que el conjunto de datos.

desv_est = np.std(df['column'])

El método std en pandastambién se puede utilizar para calcular la desviación estándar de un conjunto de datos.

Desviación media absoluta (MAD): el valor medio absoluto de la distancia entre cada punto de datos y la media.

print(f'Max: Rs.{df.column.max()}')
print(f'Min: Rs.{df.column.min()}')
print(f'Rango: Rs.{df.column.max() - df.column.min()}')

print(f'Varianza: Rs.{df.column.var().round(2)}')
print(f'Desviación Estándar: Rs.{df.column.std().round(2)}')
print(f'Desviación Media Absoluta: Rs.{(df.column - df.column.mean()).abs().mean().round(2)}')

Oblicuidad

En teoría de la probabilidad y estadística, la asimetría es una medida de la asimetría de la variable en el conjunto de datos con respecto a su media. El valor de asimetría puede ser positivo, negativo o indefinido. El valor de asimetría nos dice si los datos son asimétricos o simétricos. A continuación se muestra una ilustración de un conjunto de datos con sesgo positivo, datos simétricos y algunos datos con sesgo negativo:

Sesgo (Skewness): Mide la asimetría de la distribución. Una distribución con sesgo positivo tiene una cola más larga hacia la derecha, mientras que un sesgo negativo indica una cola más larga hacia la izquierda.

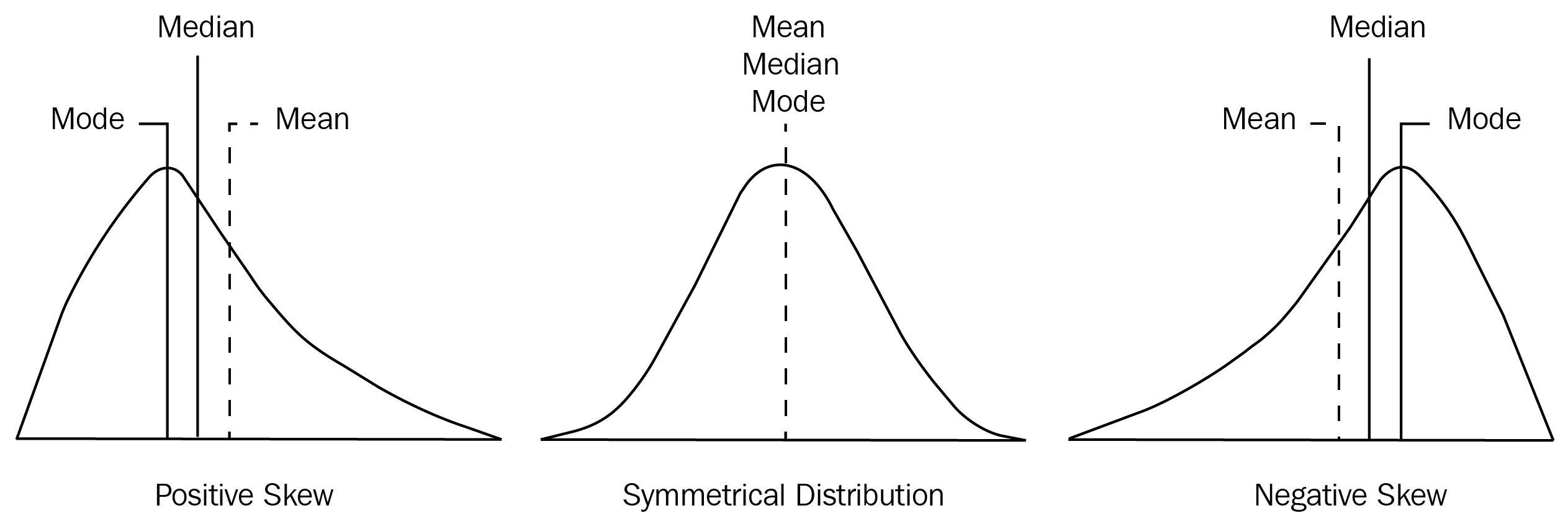
Oblicuidad

Tenga en cuenta las siguientes observaciones del diagrama anterior:

El gráfico del lado derecho tiene una cola que es más larga que la cola del lado derecho. Esto indica que la distribución de los datos está sesgada hacia la izquierda. Si selecciona cualquier punto en la cola más larga de la izquierda, la media es menor que la moda. Esta condición se conoce como asimetría negativa.
El gráfico del lado izquierdo tiene una cola que es más larga en el lado derecho. Si selecciona cualquier punto en la cola derecha, el valor medio es mayor que la moda. Esta condición se conoce como asimetría positiva.
El gráfico del medio tiene una cola derecha que es igual que la cola izquierda. Esta condición se conoce como condición simétrica.

Diferentes bibliotecas de Python tienen funciones para obtener la asimetría del conjunto de datos. La biblioteca SciPy tiene la función scipy.stats.skew(dataset). Usando la biblioteca pandas , podemos calcular la asimetría en nuestro marco de datos usando la función

df.skew()

Además, también podemos calcular la asimetría a nivel de columna. Por ejemplo, la inclinación de la altura de la columna se puede calcular utilizando el método . función.df.loc[:,”height”].skew()

Curtosis:

La curtosis es una medida estadística que ilustra en qué medida las colas de la distribución difieren de las de una distribución normal. Esta técnica puede identificar si una distribución determinada contiene valores extremos.

Pero espera, ¿no es eso similar a lo que hacemos con la asimetría? No precisamente. La asimetría normalmente mide la simetría de la distribución dada. Por otro lado, la curtosis mide el peso de las colas de distribución.

La curtosis, a diferencia de la asimetría, no se trata de picos o planitud. Es la medida de la presencia de valores atípicos en una distribución determinada. Tanto la curtosis alta como la baja son un indicador de que los datos necesitan más investigación. Cuanto mayor es la curtosis, mayores son los valores atípicos.

Tipos de curtosis

Hay tres tipos de curtosis: mesocúrtica, leptocúrtica y platicúrtica. Veamos estos uno por uno:

Mesocúrtico : si algún conjunto de datos sigue una distribución normal, sigue una distribución mesocúrtica. Tiene curtosis alrededor de 0.
Leptocúrtico : en este caso, la distribución tiene curtosis mayor que 3 y las colas gruesas indican que la distribución produce más valores atípicos.
Platicúrtica: En este caso, la distribución tiene curtosis negativa y las colas son muy delgadas en comparación con la distribución normal.

Los tres tipos de curtosis se muestran en el siguiente diagrama:

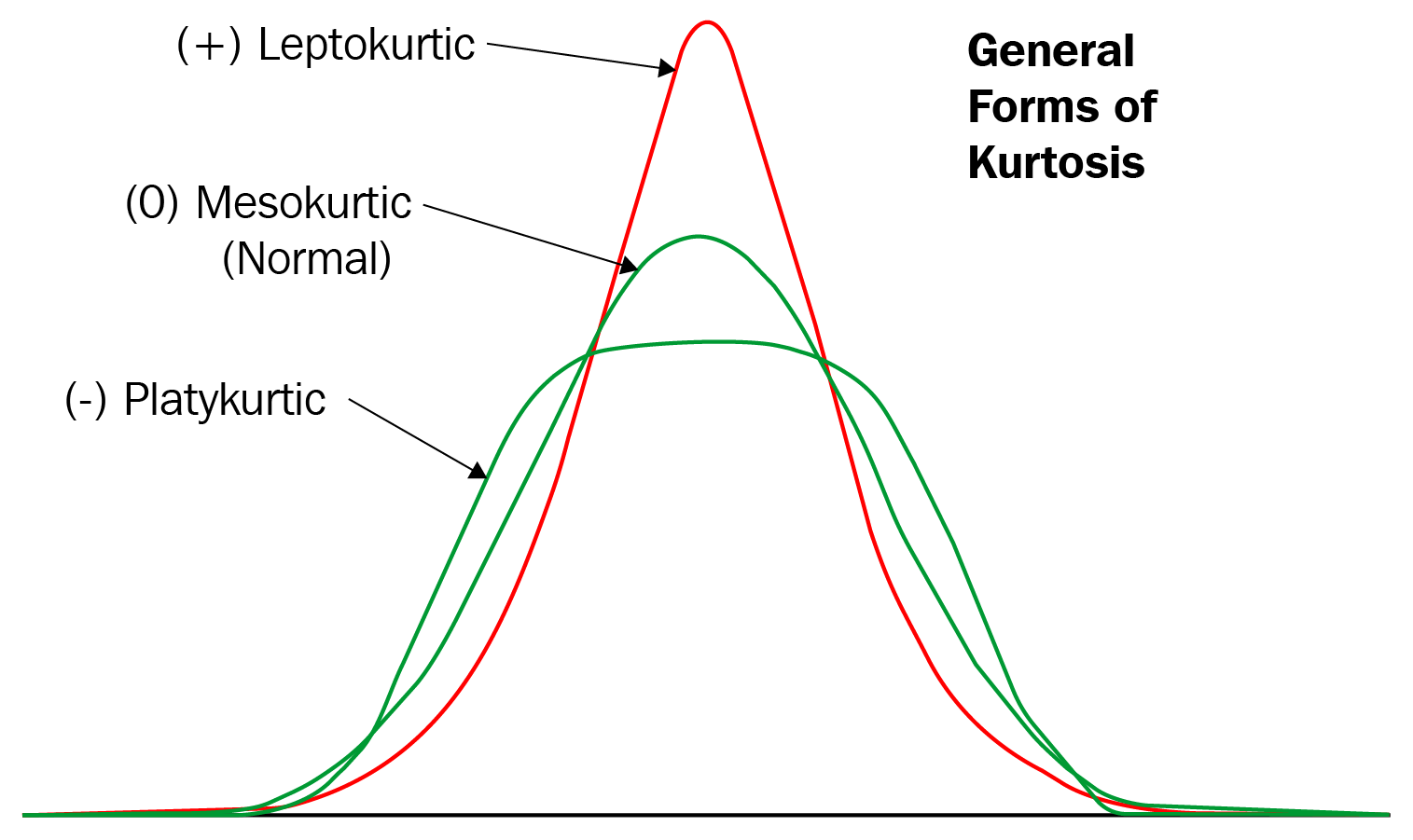
Tipos de Curtosis

Diferentes bibliotecas de Python tienen funciones para obtener la curtosis del conjunto de datos. La biblioteca SciPy tiene la función scipy.stats.kurtosis(dataset) . Usando la biblioteca pandas , calculamos la curtosis de nuestro marco de datos usando la función:

# Kurtosis of data in data using skew() function
kurtosis =df.kurt()
print(kurtosis)

# Kurtosis of the specific column
sk_height=df.loc[:,"height"].kurt()
print(sk_height)

De manera similar, podemos calcular la curtosis de cualquier columna de datos en particular. Por ejemplo, podemos calcular la curtosis de la altura de la columna como df.loc[:,”height”].kurt().

Calcular percentiles

Los percentiles miden el porcentaje de valores en cualquier conjunto de datos que se encuentran por debajo de un determinado valor. Para calcular percentiles, debemos asegurarnos de que nuestra lista esté ordenada. Un ejemplo sería si dijeras que el percentil 80 de los datos es 130: entonces, ¿qué significa eso? Bueno, simplemente significa que el 80% de los valores están por debajo de 130. La formula es:

percentil de x = (numero de valores menores de x / total de numeros observados) * 100

Supongamos que tenemos los datos dados: 1, 2, 2, 3, 4, 5, 6, 7, 7, 8, 9, 10. Entonces el valor percentil de 4 = (4/12) * 100 = 33,33%. Esto simplemente significa que el 33,33% de los datos son menores que 4.

# Pandas 0.5, 0.25, 0.75
percentil = df.quantile(0.5)
# Numpy - Calcular el percentil 50% 
percentil = np.percentile(df['column'], 50,)

Comprobación de los cuartiles de un conjunto de datos

El cuartil es como el percentil porque se puede utilizar para medir la dispersión e identificar el centro de unconjunto de datos. Los percentiles y cuartiles se llaman cuantiles. Mientras que el percentil divide el conjunto de datos en 100 porciones iguales, el cuartil divide el conjunto de datos en 4 porciones iguales. Normalmente, tres cuartiles dividirán su conjunto de datos en cuatro porciones iguales.

Cuartiles

Dado un conjunto de datos ordenado en orden ascendente, los cuartiles son los valores que dividen el conjunto de datos dado en cuartos. Los cuartiles se refieren a los tres puntos de datos que dividen el conjunto de datos dado en cuatro partes iguales, de modo que cada división representa el 25% del conjunto de datos. En términos de percentiles, el percentil 25 se denomina primer cuartil (Q1), el percentil 50 se denomina segundo cuartil (Q2) y el percentil 75 se denomina tercer cuartil (Q3).

Rango Intercuartílico (IQR):
Es la diferencia entre el tercer cuartil (Q3) y el primer cuartil (Q1). Ofrece una medida de la dispersión central y es menos sensible a outliers.

El IQR es una estadística muy útil, especialmente cuando necesitamos identificar dónde se encuentra el 50% central de los valores de un conjunto de datos. A diferencia del rango, que puede verse sesgado por números muy altos o bajos (valores atípicos), el IQR no se ve afectado por los valores atípicos ya que se centra en el medio 50. También es útil cuando necesitamos calcular valores atípicos en un conjunto de datos.

Según el cuartil, existe otra medida llamada rango intercuartil que también mide la variabilidad en el conjunto de datos. Se define de la siguiente manera:

IQR = Q3 - Q1

El IQR no se ve afectado por la presencia de valores atípicos.

column = df.column.sort_values()

# Pandas
Q1 = df.column.quantile(q=0.25)
Q1 = df.column.quantile(q=0.50)
Q1 = df.column.quantile(q=0.75)

# Numpy
Q1 = np.percentile(column, 25)
Q2 = np.percentile(column, 50)
Q3 = np.percentile(column, 75)

# rango intercuartilico
IQR = Q3 - Q1


from scipy import stats
IQR = stats.iqr(df['colum'])

Visualizar cuartiles

Si queremos trazar el diagrama de caja para un solo sujeto, podemos hacerlo usando la función plt.boxplot()

plt.boxplot(serie, showmeans=True, whis = 99)

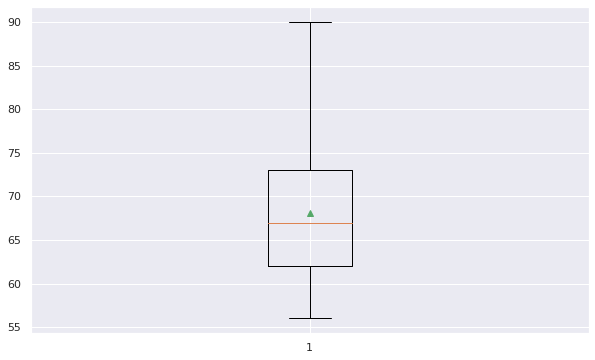
Diagrama de Caja

El diagrama anterior ilustra el hecho de que la caja va del cuartil superior al inferior (alrededor de 62 y 73), mientras que los bigotes (las barras que se extienden desde la caja) van hasta un mínimo de 56 y un máximo de 90. La línea roja es la mediana (alrededor de 67), mientras que el pequeño triángulo (color verde) es la media.

Ahora, agreguemos también diagramas de caja para otros temas. Podemos hacer esto fácilmente combinando todas las puntuaciones en una sola variable:

box = plt.boxplot(scores, showmeans=True, whis=99)

plt.setp(box['boxes'][0], color='blue')
plt.setp(box['caps'][0], color='blue')
plt.setp(box['caps'][1], color='blue')
plt.setp(box['whiskers'][0], color='blue')
plt.setp(box['whiskers'][1], color='blue')

plt.setp(box['boxes'][1], color='red')
plt.setp(box['caps'][2], color='red')
plt.setp(box['caps'][3], color='red')
plt.setp(box['whiskers'][2], color='red')
plt.setp(box['whiskers'][3], color='red')

plt.ylim([20, 95]) 
plt.grid(True, axis='y') 
plt.title('Distribution of the scores in three subjects', fontsize=18) 
plt.ylabel('Total score in that subject') 
plt.xticks([1,2,3], ['Physics','Literature','Computer'])

plt.show()

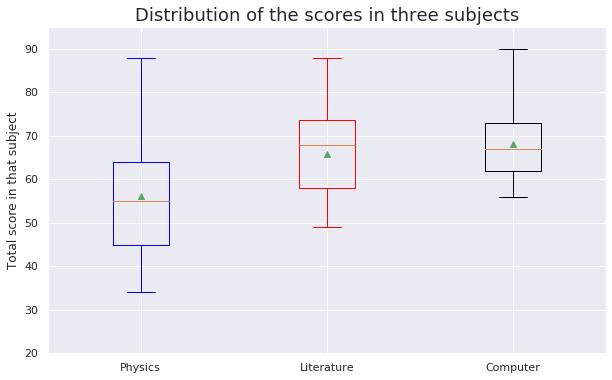
Diagrama de Caja

Del gráfico se desprende que la puntuación mínima obtenida por los estudiantes rondaba el 32, mientras que la puntuación máxima obtenida era 90, que fue en la asignatura de informática.

Agrupación de conjuntos de datos

Durante el análisis de datos, a menudo es esencial agrupar o agrupar datos según ciertos criterios. Por ejemplo, una tienda de comercio electrónico podría querer agrupar todas las ventas que se realizaron durante el período navideño o los pedidos que se recibieron el Black Friday. Estos conceptos de agrupación ocurren en varias partes del análisis de datos.

La funcion goupby() proporciona funcionalidades que nos permiten dividir, aplicar y combinar en todo el marco de datos.

Mecánica grupal

Mientras trabajamos con los pandasmarcos de datos, nuestro análisis puede requerir que dividamos nuestros datos según ciertos criterios. Los mecánicos de Groupby acumulan nuestro conjunto de datos en varias clases en las que podemos realizar ejercicios y realizar cambios, como los siguientes:

Agrupar por características, jerárquicamente
Agregar un conjunto de datos por grupos
Aplicar funciones de agregación personalizadas a grupos
Transformar un conjunto de datos en grupo

El método pandas groupby realiza dos funciones esenciales:

Divide los datos en grupos según algunos criterios.
Aplica una función a cada grupo de forma independiente.

# Group the dataset by the column body-style
style = df.groupby('body-style')

# Get values items from group with value convertible 
style.get_group("convertible")

# formar grupos basados ​​en múltiples categorías
df.groupby(["body-style","drive-wheels"])

No solo podemos agrupar el conjunto de datos con criterios específicos, sino que también podemos realizar operaciones aritméticas directamente en todo el grupo al mismo tiempo e imprimir el resultado como una serie o marco de datos. Existen funciones como max(), min(), mean(), first() y last() que se pueden aplicar directamente al objeto GroupBy para obtener estadísticas resumidas para cada grupo.

# max() will print the maximum entry of each group 
style['normalized-losses'].max()

# min() will print the minimum entry of each group 
style['normalized-losses'].min()

# calcular la media de todas las variables cuantitativas
style.mean()

Tenga en cuenta que podemos obtener el promedio de las variables de un dataframe agrupando solo por uno de los valores de una columna categorica, de la siguiente manera:

# La varibale style tiene como valor el dataframe agrupado por body-style
style.get_group("convertible").mean()

También podemos aplicar count() a variables del dataframe agrupado:

style['column'].count()

Data agregation

La agregación es el proceso de implementar cualquier operación matemática en un conjunto de datos o un subconjunto del mismo. La agregación es una de las muchas técnicas de pandas que se utiliza para manipular los datos en el marco de datos para el análisis de datos.

La función df.aggregate() se utiliza para aplicar agregación en una o más columnas. Algunas de las agregaciones más utilizadas son las siguientes:

sum: Devuelve la suma de los valores del eje solicitado
min: Devuelve el mínimo de los valores para el eje solicitado
max: Devuelve el máximo de los valores para el eje solicitado

Dado que la agregación solo funciona con columnas de tipo numérico, se debe agrupar por columnas numéricas del conjunto de datos y les apliquemos algunas funciones de agregación:

# filtrar el dataset agrupado por colummnas numericas
new_dataset = df.filter(["length","width","height","curb-weight","price"],axis=1)

# applying single aggregation for mean over the columns
new_dataset.agg("mean", axis="rows")

# encontrar la suma y el mínimo de todas las columnas a la vez  
new_dataset.agg(['sum', 'min']) 

El resultado es un marco de datos con filas que contienen el resultado de la agregación respectiva que se aplicó a las columnas. Para aplicar funciones de agregación en diferentes columnas, puede pasar un diccionario con una clave que contenga los nombres de las columnas y los valores que contengan la lista de funciones de agregación para cualquier columna específica:

# find aggregation for these columns 
new_dataset.aggregate({"length":['sum', 'min'], 
              "width":['max', 'min'], 
              "height":['min', 'sum'], 
              "curb-weight":['sum']}) 
# if any specific aggregation is not applied on a column
# then it has NaN value corresponding to it

El resultado del código anterior es el siguiente:

	length	width	height	curb-weight
max	NaN	1.0000	NaN	NaN
min	0.678039	0.8375	47.8	NaN
sum	168.257568	NaN	10807.1	513689.0

Operaciones grupales

Las operaciones más importantes implementadas por groupBy son agregar, filtrar, transformar y aplicar. Una forma eficaz de implementar funciones de agregación en el conjunto de datos es hacerlo después de agrupar las columnas requeridas. La función agregada devolverá un único valor agregado para cada grupo. Una vez creados estos grupos, podemos aplicar varias operaciones de agregación a esos datos agrupados.

# Group the data frame df by body-style and drive-wheels and extract stats from each group
df.groupby(["body-style","drive-wheels"]).agg(
    {
         'height':min, # minimum height of car in each group
         'length': max, # maximum length of car in each group
         'price': 'mean', # average price of car in each group
        
    }
)
# Podemos crear un diccionario de agregación de funciones que queremos realizar en grupos y luego usarlo más tarde:
aggregations=(
    {
         'height':min, # minimum height of car in each group
         'length': max, # maximum length of car in each group
         'price': 'mean', # average price of car in each group
        
    }
)
# implementing aggregations in groups
df.groupby(
   ["body-style","drive-wheels"]
).agg(aggregations) 

numpy tambien tiene funciones de agregacion que podemos utilizar con groupby:

import numpy as np

df.groupby(
   ["body-style","drive-wheels"])["price"].agg([np.sum, np.mean, np.std])

Visualización de variables cuantitativas

Si bien las estadísticas resumidas son ciertamente útiles para explorar y cuantificar una característica, puede que nos resulte difícil concentrarnos en un montón de números. Es por eso que la visualización de datos es un elemento tan poderoso de EDA.

Para variables cuantitativas, los diagramas de caja y los histogramas son dos visualizaciones comunes. Estos gráficos son útiles porque comunican simultáneamente información sobre los valores mínimos y máximos, la ubicación central y la dispersión. Los histogramas también pueden iluminar patrones que pueden afectar un análisis (por ejemplo, sesgo o multimodalidad).

La biblioteca de Python seaborn, construida sobre matplotlib, ofrece las funciones boxplot() y histplot() para trazar fácilmente datos desde un DataFrame de pandas:

Histogramas: Permiten visualizar la distribución de frecuencias de una variable continua, identificando modas, asimetrías y la forma general de la distribución.
Diagramas de caja (Boxplots): Ofrecen una representación visual de la mediana, los cuartiles y los valores atípicos, y son útiles para comparar distribuciones y detectar outliers.
Gráficos de barras: Son útiles para datos categóricos, mostrando la frecuencia o proporción de cada categoría.

Los resúmenes univariados son esenciales para cualquier análisis de datos, ya que proporcionan los fundamentos para entender cada variable individualmente antes de explorar las relaciones entre múltiples variables.

Variables categoricas

Value Counts para Datos Categoricos

Cuando se trata de variables categóricas, las medidas de tendencia central y dispersión que funcionaron para describir variables numéricas, como la media y la desviación estándar, generalmente se vuelven inadecuadas cuando se trata de valores discretos. A diferencia de los números, los valores categóricos no son continuos y muchas veces no tienen un orden intrínseco.

En cambio, una buena manera de resumir las variables categóricas es generar una tabla de frecuencia que contenga el recuento de cada valor distinto. Por ejemplo, puede que nos interese saber cuántos de los listados de alquileres de la ciudad de Nueva York pertenecen a cada distrito. Relacionado, también podemos encontrar qué municipio tiene más listados.

Pandas ofrece el método .value_counts() para generar los recuentos de todos los valores en una columna de DataFrame. Tambien podemos ver los primeros 30 valores mas grandes usando la funcion nlargest()

Proporciones de valor para datos categóricos

Una tabla de recuentos es un enfoque para explorar variables categóricas , pero a veces es útil observar también la proporción de valores en cada categoría. Por ejemplo, saber que hay 3.539 listados de alquileres en Manhattan es difícil de interpretar sin ningún contexto sobre los recuentos en las otras categorías. Por otro lado, saber que los listados de Manhattan representan el 71% de todos los listados de la ciudad de Nueva York nos dice mucho más sobre la frecuencia relativa de esta categoría.

Podemos calcular la proporción de cada categoría dividiendo su recuento por el número total de valores de esa variable:

dataframe.column.value_counts() / len(dataframe.column)

Visualización de variables categóricas

Para las variables categóricas , los gráficos de barras y los gráficos circulares son opciones comunes para visualizar el recuento (o proporción) de valores en cada categoría. También pueden transmitir las frecuencias relativas de cada categoría.

La biblioteca de Python seaborn ofrece varias funciones que pueden crear gráficos de barras. La forma más sencilla de trazar los recuentos es countplot():

Variables Categóricas Ordinales - Tendencia Central

Las variables categóricas ordinales tienen categorías ordenadas. Para las variables categóricas ordinales , podemos encontrar la categoría modal como en el ejercicio anterior, pero también podemos calcular otras estadísticas de resumen que no son posibles para las variables categóricas nominales. Para tendencia central, esto significa que también podemos calcular una mediana.

Para calcular estadísticas numéricas para categorías ordenadas, primero debemos asignar valores numéricos a las categorías. Considere la variable educationde los datos del censo. Podemos inspeccionar las categorías únicas en esta variable usando .unique():

print(list(df['education'].unique()))

Salida:

['HS-grad', 'Some-college', '7th-8th', '10th', 'Doctorate', 'Prof-school', 'Bachelors', 'Masters', '11th', 'Assoc-acdm', 'Assoc-voc', '1st-4th', '5th-6th', '12th', '9th', 'Preschool']

Luego, podemos asociar cada una de estas categorías con un valor numérico, que indica el “nivel educativo” de un individuo. En Python, la forma más sencilla de hacer esto es convertir la variable a tipo ‘category’usando pandas.Categorical(). Al convertir una columna a tipo ‘category’, también podemos pasar una lista con las categorías de la columna (y utilizando el parámetro ordered=True ) para indicar el orden deseado.

correct_order = ['Preschool', '1st-4th', '5th-6th', '7th-8th', '9th', '10th', '11th', '12th', 'HS-grad', 'Some-college', 'Assoc-voc', 'Assoc-acdm', 'Bachelors', 'Masters', 'Prof-school', 'Doctorate']

df['education'] = pd.Categorical(df['education'], correct_order, ordered=True)

Las variables almacenadas como categoría de tipo tienen un atributo ( cat.codes) que convierte las categorías en números. Esto nos permite realizar operaciones numéricas en este campo categórico. Esto nos permite calcular la categoría mediana usando la función median() de numpy:

median_index = np.median(df['education'].cat.codes)
print(median_index) # Output: 9

median_category = correct_order[int(median_index)]
print(median_category) # Output: Some college

Al usar .cat.codes en education, podemos calcular que el valor medio para el nivel educativo es ‘9’lo que se traduce en ‘Some college’.

En el ejercicio anterior, solíamos utilizar .cat.codes para encontrar la categoría mediana para una variable categórica ordinal. Podemos usarlo cat.codespara devolver valores numéricos y también realizar una amplia gama de operaciones con datos categóricos. Sin embargo, antes de realizar cualquier operación, debe verificar que tengan sentido en el contexto de los datos.

Por ejemplo, recuerde que las categorías para education(en orden) son las siguientes:

education_levels_ordered = ['Preschool', '1st-4th', '5th-6th', '7th-8th', '9th', '10th', '11th', '12th','HS-grad', 'Some-college', 'Assoc-voc', 'Assoc-acdm', 'Bachelors', 'Masters', 'Prof-school', 'Doctorate']

Si bien podemos representar estas categorías con números igualmente espaciados, no existe un espaciado igual entre categorías. Algunas brechas entre los niveles educativos representan hasta cuatro años adicionales de escolaridad (por ejemplo, ‘1.º-4.º’ a ‘5.º-6.º’), mientras que otras representan un solo año adicional de escolaridad (por ejemplo, del ‘9.º’ al ‘10.º’).

Cuando utilizamos .cat.codes para traducir estas categorías a números enteros, esos números enteros tienen el mismo espacio. Si bien a menudo es necesario traducir categorías a números para almacenar y usar el orden de las categorías (para calcular una estadística como la mediana, que solo se basa en el orden, no en el espaciado), no debemos usar esos números para calcular estadísticas , como la media. - para los cuales la distancia entre valores importa.

En la práctica, los investigadores a veces (aunque incorrectamente) informan medias para categorías ordinales. Por ejemplo, un investigador podría querer analizar las respuestas de una encuesta a la pregunta “Califica tu felicidad en una escala del 1 al 5, donde 1 significa ‘muy infeliz’ y 5 significa ‘muy feliz’”.

Si ese investigador calcula la ‘puntuación media de felicidad’, está asumiendo que la diferencia de felicidad entre una calificación de 1 y 2 es la misma que la diferencia de felicidad para una calificación de 3 y 4. En la práctica, esta suposición probablemente no sea cierta. y debe reconocerse si se informa una media de una variable categórica ordinal.

Categorías ordinales: Propagación

En el último ejercicio, aprendimos que la media no es interpretable para variables categóricas ordinales porque la media se basa en el supuesto de un espaciado igual entre categorías.

Muchas otras estadísticas que normalmente usaríamos para datos numéricos se basan en la media. Por este motivo, estas estadísticas no son apropiadas para datos ordinales. Recuerde que la desviación estándar y la varianza dependen de la media; sin una media, ¡tampoco podemos tener una desviación estándar o una varianza confiable!

En cambio, podemos confiar en otras estadísticas resumidas, como la proporción de los datos dentro de un rango o percentiles/cuantiles. Por ejemplo, considere la variable educación de antes. Para calcular un rango que contiene el 80% de los datos, podemos usar np.percentile():

tenth_perc_ind = np.percentile(df['education'].cat.codes, 10)
tenth_perc_cat = correct_order[int(tenth_perc_ind)]
print(tenth_perc_cat) # output: 11th
 
nintieth_perc_ind = np.percentile(df['education'].cat.codes, 90)
nintieth_perc_cat = correct_order[int(nintieth_perc_ind)]
print(nintieth_perc_cat): #output: Bachelors

Esto nos dice que al menos el 80% de los encuestados tienen un “nivel educativo” desde el 11º grado hasta una licenciatura.

Tabla de proporciones

Ya has visto que podemos usar la función .value_counts() para obtener una tabla de frecuencias para una variable categórica. Una tabla de frecuencias suele ser el primer enfoque que un científico de datos podría utilizar para resumir una variable categórica; sin embargo, a veces resulta útil observar la proporción de valores en cada categoría.

Por ejemplo, saber que hay 14976 personas en el conjunto de datos del censo que están casadas con un cónyuge civil es difícil de interpretar sin el contexto de conocer las cifras de las otras categorías. En cambio, si sabemos que el 32% de la población encuestada está casada con un cónyuge civil, tenemos más contexto sobre la frecuencia relativa de esta categoría. Podemos calcular proporciones dividiendo la frecuencia por el número de observaciones en los datos.

df['education'].value_counts()/len(df['education'])

También podemos calcular proporciones usando .value_counts() estableciendo el parámetro normalize igual a True:

df['education'].value_counts(normalize = True).head()

Salida:

HS-grad         0.322502
Some-college    0.223918
Bachelors       0.164461

Tabla de proporciones: datos faltantes

Una cosa a tener en cuenta al calcular la proporción de datos en una categoría particular: ¿cómo se manejan los datos faltantes? Por ejemplo, considere la variable workclass de los datos del censo. Esta columna contiene 1836 valores faltantes, codificados como NaN. De forma predeterminada, esos valores faltantes no se cuentan con .value_counts().

Por lo tanto, los resultados de los codigos vistos anteriormente serán ligeramente diferentes. Puede configurar el parámetro dropna para que .value_counts() determine cómo se manejan los valores NaN en los resúmenes de datos.

Cuando dividimos la frecuencia de cada categoría por len(df['workclass']), calculamos la proporción de un grupo workclass específico como parte de todas las personas en el conjunto de datos. Esto equivale a configurar dropna = False cuando se llama a .value_counts().

df.workclass.value_counts(dropna = False, normalize = True)

Salida

Private             0.697030
Self-emp-not-inc    0.078038
Local-gov           0.064279
NaN                 0.056386
State-gov           0.039864
Self-emp-inc        0.034274
Federal-gov         0.029483
Without-pay         0.000430
Never-worked        0.000215

Aquí, vemos que al 5,6% de los encuestados tienen valores faltantes. Por el contrario, usar .value_counts(normalize = True) o .value_counts(normalize = True, dropna = True) para ser explícito devuelve la proporción de un workclassgrupo específico como parte de las personas en el conjunto de datos que respondieron a esta pregunta.

df.workclass.value_counts(normalize = True)

Salida

Private             0.738682
Self-emp-not-inc    0.082701
Local-gov           0.068120
State-gov           0.042246
Self-emp-inc        0.036322
Federal-gov         0.031245
Without-pay         0.000456
Never-worked        0.

Tenga en cuenta que si no incluimos los valores faltantes en nuestro denominador, observamos proporciones ligeramente mayores en cada categoría (y en ninguna NaNcategoría) en el resultado anterior. Es importante pensar en cómo desea tratar los datos faltantes al resumir una variable categórica y luego interpretar los valores resultantes de manera adecuada.

Variables categóricas binarias

Las variables categóricas binarias tienen sólo dos categorías. En Python, estas variables suelen codificarse como 0 - 1 o True - False. Esto facilita el cálculo de la frecuencia/proporción de estas variables en un conjunto de datos. Por ejemplo, considere una variable income_>50K, que es igual a 1 si una persona gana más de 50.000 dólares al año, y 0 en caso contrario. Si sumamos todos los 1s y 0s en esta columna, la suma será exactamente igual al número de 1s (personas que ganan más de 50k):

np.sum(df['income_>50K'])  #output: 7841

En Python, el mismo comportamiento se aplica a las columnas codificadas como True/ False porque True son forzadas 1 y False forzadas 0 (esto también es cierto en la mayoría de los otros lenguajes de programación utilizados por los científicos de datos). De manera similar, podemos calcular la proporción igual 1 o True tomando la media de la columna. Esto funciona porque la media es solo la suma de todos los valores de la columna (que es la frecuencia de 1 s o Trues) dividida por el número de valores de la columna:

np.mean(df['income_>50K'])  #output: 0.24

Finalmente, podemos hacer uso de este ingenioso truco para cualquier variable usando un condicional para traducir una variable no binaria a valores Truey False. Por ejemplo, recuerde la workclassvariable del ejercicio anterior. Supongamos que desea calcular el número (o proporción) de personas que trabajan en el gobierno local. Podríamos traducir la workclasscolumna a una variable binaria que indique si una persona trabaja en el gobierno local ( True) o no ( False) usando un condicional.

print(df.workclass == 'Local-gov')

Salida

      False
      True
      True
      False
      False

Luego, podemos usar la suma o media para calcular una frecuencia o proporción de Trues en los datos.

(df.workclass == 'Local-gov').sum()  #output: 2093
(df.workclass == 'Local-gov').mean() #output: 0.064