El teorema del límite central

El teorema del límite central (TLC) es un principio fundamental en estadística que describe el comportamiento de la distribución de las medias muestrales de poblaciones.

Establece que, dadas ciertas condiciones, la distribución de las medias muestrales de un gran número de muestras independientes y aleatorias de una población tiende a ser una distribución normal (también conocida como distribución gaussiana), independientemente de la forma de la distribución original de la población. Es la base para pruebas de hipótesis comunes, como las pruebas Z y t.

Implicaciones:

1. Normalidad: La distribución de las medias muestrales será aproximadamente normal si se cumple una de las siguientes condiciones:
   • La población de la que se extraen las muestras es ya normal.
   • El tamaño de muestra es suficientemente grande, generalmente más de 30. Sin embargo, un tamaño de muestra más pequeño puede ser suficiente si la distribución de la población no se aleja mucho de la normalidad.
2. Media y varianza:
   • La media de la distribución de las medias muestrales es igual a la media de la población original.
   • La varianza de la distribución de las medias muestrales es igual a la varianza de la población dividida entre el tamaño de la muestra.
3. Error estándar:
   • La desviación estándar de la distribución de las medias muestrales se llama error estándar de la media y se calcula como:
   \[\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}},\]

   donde:

   • \(sigma\): Desviación estándar de la población.
   • \(n\): Tamaño de la muestra.

Desarrollar la intuición para el CLT

Imagine que un científico de datos quiere saber el salario medio por hora de todos los adultos estadounidenses que trabajan y ganan menos de 150 dólares por hora. Se trata de una población muy grande; no sería realista recopilar datos salariales para cada persona que cumple estos criterios. En cambio, supongamos que el científico de datos encuesta una muestra aleatoria de 150 personas, registra el salario por hora de cada persona y calcula una media muestral de 17,74 dólares por hora. Aquí hay un histograma de esta muestra, con una línea de puntos negra en 17,74:

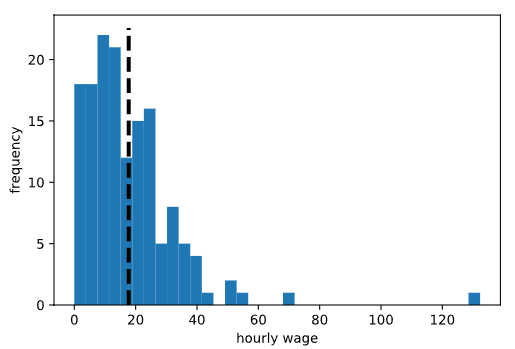
Un buen científico de datos sabe que la media de esta muestra no es EXACTAMENTE la misma que la media de la población, pero espera que sea SUFICIENTEMENTE cercana. La siguiente pregunta es:

¿A qué distancia de la media poblacional podría estar de manera realista esta muestra?

Para responder a esto, supongamos temporalmente que lo sabemos todo y que, de hecho, podemos inspeccionar los salarios por hora de todas las personas de la población de interés. Supongamos que el salario promedio real es de 18,84 dólares por hora y un histograma de la población total se ve así:

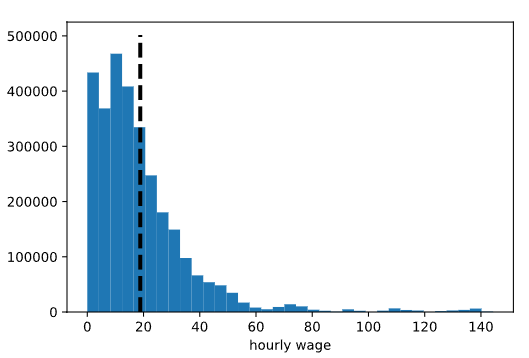
En la vida real, normalmente solo observamos una muestra, pero para cuantificar nuestra incertidumbre sobre esa muestra, es útil pensar en lo que sucedería si pudiéramos observar más. Considere el siguiente experimento mental: imagine que podemos tomar un gran número (digamos, 10 000) de muestras aleatorias de 150 personas de la población y calcular el salario medio por hora para cada una de esas muestras. Luego podríamos inspeccionar las 10 000 medias muestrales para ver cuánto varían. Una gran cantidad de variación nos haría menos seguros de que cualquier media de muestra individual sea representativa de la población; Menos variación nos daría más confianza.

El siguiente código Python hace esto en un bucle. El objeto population es una lista que contiene todos los salarios de la población total. En cada iteración del ciclo, hacemos lo siguiente:

• tomar una muestra aleatoria de 150 salarios de la población
• almacenar la media muestral en una lista llamada sample_means

Finalmente, después de recolectar 10.000 medias de muestra, podemos inspeccionarlas mediante un histograma.

import numpy as np
import matplotlib.pyplot as plt
import random

sample_means = []

for i in range(10000):
    samp = random.sample(population, 150)
    sample_means.append(np.mean(samp))

plt.hist(sample_means, bins = 30)
plt.vlines(np.mean(sample_means), 0, 1000, lw=3, linestyles='dashed')

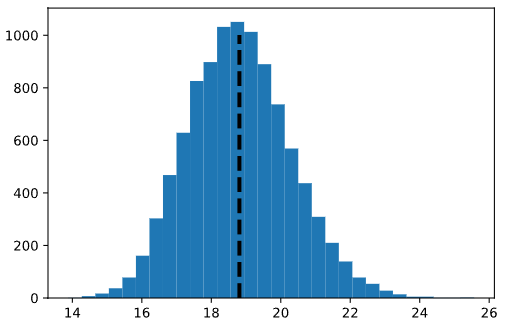
Hay algunas cosas interesantes a notar acerca de esta distribución, que se llama distribución muestral de la media :

• A diferencia de la distribución de la población, que está muy sesgada a la derecha, esta distribución tiene (casi) una distribución normal: simétrica con una sola moda.
• El promedio de las medias muestrales (línea de puntos negra) es aproximadamente igual a la media poblacional (18,84).
• Las medias de la muestra de 10.000 oscilan aproximadamente entre 14 y 24 (más o menos 5 dólares de la media real).

Específicamente, la función NumPy percentile() se puede utilizar para calcular que el 95% de las medias de la muestra de la simulación anterior se encuentran en un rango de 16,14 a 21,87 dólares por hora (más o menos alrededor de 2,87 dólares de la media):

percentiles = np.percentile(sample_means, [2.5, 97.5])
print(percentiles)
# output: array([16.13810156, 21.87180969])

Definición formal del CLT

Ahora es el momento de definir formalmente el CLT, que nos dice que la distribución muestral de la media:

• Se distribuye normalmente (para un tamaño de muestra suficientemente grande (>=30)).
• Está centrado en la media poblacional.
• Tiene una desviación estándar igual a la desviación estándar de la población dividida por la raíz cuadrada del tamaño de la muestra. Esto se llama error estándar.

Con respecto a la fórmula del error estándar descrita anteriormente, tenga en cuenta que hay dos palancas en el ancho de la distribución muestral:

• La desviación estándar de la población. Las poblaciones con mayor variación producirán medias muestrales con mayor variación. Por ejemplo, imagine muestrear las alturas de niños de 5 años en comparación con el muestreo de alturas de niños de 5 a 18 años. Hay más variación en las alturas de los niños de 5 a 18 años, por lo que habrá más variación en las muestras individuales.

• El tamaño de la muestra. Cuanto mayor sea el tamaño de la muestra, menor será la variación en las medias de muestras repetidas. En el ejemplo de salario anterior, imagine muestrear solo a cinco personas en lugar de 150. Esas cinco personas muestreadas podrían incluir un valor atípico que desvíe toda la media de la muestra. Si tomamos una muestra de 150 (o incluso más) personas, es más probable que tengamos valores atípicos altos y bajos que se anulan entre sí.